О ВЧ СТАБИЛИЗАЦИИ ЖЕЛОБКОВОЙ НЕУСТОЙЧИВОСТИ
Взаимодействие низкочастотных желобковых колебании и высокочастотных учитывается через изменение частоты и)вч при развитии желобковых возмущений. В силу постоянства адиабатического инварианта ВЧ колебаний И'вч/швч вариации (оВч вызывают изменения 1Увч.
Учет этого обстоятельства позволяет получить простые критерии стабилизации желобковой неустойчивости. Исследуется модель плазмы с резкой границей. Рассмотрены ВЧ колебания, имеющие вид: собственных колебаний вакуумного промежутка между плазмой и стенкой камеры; колебаний, поддерживаемых ВЧ антенной; собственных поверхностных мод, локализованных у резкой границы плазмы.
Успешные эксперименты по стабилизации желобковой неустойчивости ВЧ полями на установке РЬаес1ги8 [1] стимулировали теоретическое исследование вопроса о влиянии ВЧ колебаний на НЧ колебания плазмы. Было выяснепо, что такое влияние осуществляется посредством: 1) понде - ромоторной силы, включающей в себя как силу, непосредственно действующую со стороны ВЧ поля на плазму, так и градиент добавочного давления, возникающего в плазме под действием ВЧ поля; 2) комбинационных полей, частота п волновой вектор которых определяются соотношениями а)±=а)=ьО, /г±=А:±д, где со, /с — частота и волновой вектор ВЧ поля, £2, д — частота и волновой вектор НЧ колебаний. Оба эти эффекта являются нелинейными, и их учет требует довольно громоздких выкладок [2—5]. что может приводить к противоречивым результатам при анализе конкретных ситуаций (см., например. [6, 7]).
В данной работе показано, что задача о влиянии ВЧ полей на НЧ колебания плазмы может быть решена в рамках Линейной Теории. Настоящий анализ основывается на том обстоятельстве, что в силу существенного различия частот ВЧ и НЧ колебаний при эволюции последних должен сохраняться адиабатический инвариант, характеризующий ВЧ степень свободы. В том случае, когда амплитуда ВЧ колебаний не слишком велика (они МоГут считаться линейными), адиабатический инвариант равен И^/со, где
IV — энергия ВЧ колебаний, ои — их частота. Если развитие НЧ возмущений вызывает изменение частоты ВЧ колебаний на бо). то их энергия меняется на &№=(£>Со/со) •УР. Плазма будет устойчивой, если энергия, которая могла бы выделиться при раскачке желобковой неустойчивости ДИ' окажется меньше 61Г. Использование этого критерия позволяет автоматически учесть оба аспекта воздействия ВЧ колебаний на НЧ, указанные выше. Хотя при расчете бсо необходимо принимать во внимание искажение профиля плотности плазмы, производимое НЧ колебаниями, во многих случаях задача оказывается значительно проще непосредственного анализа нелинейного взаимодействия НЧ и ВЧ колебаний, как это делалось ранее.
Значительное упрощение задачи, рассматриваемой в настоящей работе, связано также с предположением о резкой границе плазмы. В разд. 1 считается, что ВЧ колебания представляют собой собственные колебания ва
Куумного промежутка между плазмой и стенкой камеры. Найдено, что для стабилизации желобковой неустойчивости ВЧ давление должно по порядку величины превышать 10ZP0LkLB, Где Р0 — давление плазмы, Ьв — характерный масштаб изменения магнитного поля, К — волновое число ВЧ колебаний. Стабилизация существенно облегчается в том случае, когда колебания с комбинационным значенпем волнового числа по OY (Kvt±=Kv±Q) Также близки к собственным колебаниям вакуумного промежутка. Здесь У — координата, вдоль которой граница плазмы модулирована желобковы - ми колебаниями, Q — волновое число модуляции. Подобное резонансное усиление воздействия ВЧ колебаний характерно для того случая, когда оно определяется комбинационными эффектами [3—5].
В разд. 2 настоящей работы считается, что ВЧ колебания поддерживаются антенной. При анализе таких колебаний вакуумный промежуток рассматривается как элемент ВЧ колебательного контура. В этом случае для стабилизации желобковой неустойчивости давление ВЧ поля по порядку величины должно превышать PQl±/LB, где 1± — характерный поперечный размер системы. Такой же вид имеет условие стабилизации, полученное В [6].
В плазме с резкой границей существуют ВЧ поверхностные моды. Поверхностные моды локализованы у границы плазмы, и поэтому с их помощью удобно воздействовать на ее колебания. К сожалению, оказывается, что энергия поверхностных мод, рассмотренных в разд. 3 настоящей работы, уменьшается при возникновении желобковых возмущений. Это означает, что такие моды непригодны для стабилизации желобковой неустойчивости, более того, их возбуждение может привести к дестабилизации устойчивой границы плазмы.
1. Собственные колебания вакуумного промежутка (граница плазмы — стенка камеры)
Реальные системы, в которых проводятся эксперименты по ВЧ стабилизации желобковой неустойчивости, аксиально-симметричны. Для упрощения анализа заменим цилиндрическую геометрию плоской. Будем считать, что стенка вакуумной камеры и граница плазмы расположены при х=0 и Х=1 соответственно. В желобковых возмущениях плазма смещается по ОХ, причем амплитуда смещения зависит от координаты У. Внешнее магнитное поле считается направленным по OZ. Предположим, что в вакуумном промежутке возбуждены ВЧ колебания с электрическим вектором, параллельным OZ: Ег(т, T)=E(X, у)ехр(—Mt). Амплитуда электрического поля удовлетворяет уравнению
Будем считать, что частота ВЧ колебаний достаточно велика, и они не проникают в глубь плазмы. Соответственно для электрического поля примем нулевые граничные условия как на поверхности камеры, так и на границе плазмы.
Рассчитаем изменение частоты собственных колебаний при модуляции границы плазмы по гармоническому закону (х=/+а Cos Qy). При плоской границе плазмы (а=0) собственные функции уравнения (1) имеют вид E(T)=Sin(Kxx)Exp(Ikvy), Где &*== ((ои/с)2—К/)ч'=ппЦ. По координате У примем периодические граничные условия Е(х, У)=Е(х, Y+2Lv), Поэтому Ку= =SnlLy, Q=RnlLy (S, Г — целые числа). Если а^О, то собственные функции представляют собой бесконечные ряды вида
Оо
Е (г)e Xi А"»sin (**.«*) ехР (* (К+Щ) у) 1
Тле кXtm—(((J}/c)г—(кv--mq)г)ъ. Считая амплитуду смещения границы достаточно малой (а<1), оставим в этой сумме слагаемые с номерами т=* =0, =Ы. Учитывая в граничном условии Е(х, У) |х»*+а со» «=0 слагаемые,
Пропорциональные Exp(Ikvy), Exp(I(Awdtg)Y), Получаем систему уравнений (—L)T,,i4e6Д«/+ (а/2) (AtkX., Cos(fcIf XL)+A-kXf cos(fcx, -iL)) ^O,
(a/2) (-i)mA0kx+A±l sin(/^ ±iO=0i
Где 6A*=O)6A)/C:ЈAx, 6O)=(D—A)n, Л„, «п, Ку=с((пп11)г+ку[88])'1г.
Из (2) Получаем
Ба)=а2А)/4/Л^х2(Ах,! Ctg(/Cx, Il)+kXt _t ctg(fc, f _,Z)). (3>
Условие стабилизации можно найти, учитывая соотношения W7A)=const И (П1.2) (см. Введение, а также Приложение 1). Имеем
Po/Lb <^j—(l+2/Nz)Nx2(kx, lctg(kxAl)+kx-ictg(kx-ll)), (4)
Ь4л
Где LB — характерный масштаб изменения магнитного поля, В~ — амплитуда ВЧ поля, NX4 „=&*, „с/со, N2=NX+Nyz.
Если параметры комбинационных колебаний с Kt, ±I Существенно отличны от собственных, то условие стабилизации (4) по порядку величины можно представить в виде
Р0<Ю~2В^2кЬв.
Стабилизирующее воздействие ВЧ поля неограниченно возрастает,, если одна из величин /с*, ±I Приближается к собственному значению краевой задачи. Предположим, например, что KXt Г»п п/1. Учтем, что частота собственных колебаний вакуумного промежутка, соответствующая набору волновых чисел (п Ky+Q), Также зависит от а. Опустим в правой части (3) второе слагаемое, а в первом заменим Ctg(&X, Il) На (kXt ,Z—П'л+бЛ*, 11)~ ГДе Цfcx. i=ь)ц(ь/czkXf ,, 6Ь> = 0)—0)n, Кш.
Модифицированное дисперсионное соотношение принимает вид
Q4-Я(fcXi Л) (К TL-Nn)-(AlkxkXt ,/2)2=0, (5)
Где Q=coЦaЙ2/сг.
При а=0 (5) позволяет определить значения двух близко расположенных собственных частот вакуумного промежутка с гладкой границей плазмы о)п, Ку (Q=0) HO)N',*»+Q (Q=—KXt J-(K^ Xl—Nn)). Если A»^_1|A*, TL—N’N, То из (5) Находим 6Co=±AKxkxt 1С2/2/ш. Линейная зависимость бо) от амплитуды возмущения, как известно, характерна для случая совпадающих частот (вырождение спектра). Одно из полученных решений убывает с ростом
А, что свидетельствует о дестабилизирующем воздействии ВЧ поля.
Предположим, что амплитуда возмущений, которые предполагается стабилизировать, не превышает АТах. Если |соп, Co«^+Q|<Ama*&«Fc*, IC2/ /2/со, то из-за неконтролируемых смещений границы при возбуждении ВЧ поля можно попасть на ветку колебаний, дестабилизирующую границу плазмы. Поэтому при выборе колебаний, используемых для стабилизации, их частоту, следует подобрать таким образом, чтобы выполнялось условие Kx~LKXt Il—N'N>Amax- Соответственно величина 6A)ma*~a2C2Ax/aT„a*Z2Ax. t, И при оптимальном подборе частоты условие стабилизации принимает приближенный вид
PJLB<BJIAna Max•
Данное условие может быть очень мягким. Однако его практическое использование затрудняется как неопределенностью в значениях амплитуд реальных флуктуаций, так и необходимостью чрезвычайно точного подбора параметров плазмы.
Вазложим поле и ток в ряд Фурье по ОУу 5-я компонента Фурье электрического поля удовлетворяет уравнению
Е,',!и+Е,((и)/с)2—ку2)— — ^ ^ 16 (х—а). (6)
|
А | Sh(X,(/—Х) )Sh(X,A) (х>а) WW9 w** х J 2пт, |
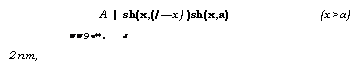
|
Ев = |
![]() При плоской границе плазмы решение (6) пропорционально функции Грина
При плоской границе плазмы решение (6) пропорционально функции Грина
X, sh(x,0 ' Sh(x^r)sh(x,(Z—A)) (X<a)
Где X,E((Ns/Ly)2— (со/C)2)
Предположим теперь, что воздействие желобковых колебаний привело к гофрировке границы плазмы подрайону X—L+A Cos (Nq У ILv+(P). Считая амплитуду гофрировки достаточно малой, учтем лишь составляющие электрического поля, пропорциональные Exp (InsylLv), Exp (In(S±Q)Y/Lv). В области (1>х>а) имеем
(л Sh(X.A)Sh(X.(I-X))
£. — I Л ---------------- —— ----------- + В, Sh (и, х)) Exp (Msi//Ly) +
X* SIlX, Јj
|
(7) |
![]() + А,Л Sh (x, i+x)exp (in (S+q)y/Lv)+Aa- sh (x,,_x)exp (in (s—q)y/LV),
+ А,Л Sh (x, i+x)exp (in (S+q)y/Lv)+Aa- sh (x,,_x)exp (in (s—q)y/LV),
Где х,,±= ((п/Ьу)2(S±Q) 2- ((д/с)2)1,2.
Из условия равенства нулю электрического поля на границе плазмы получаем
А аА ехр(±1Ф)эЬ(х, а)
„ А 1А. , . . зЬ(х, а)
В, --------- т-[х,>+ с1Ь(хл>+/)+х,,_ сИЦх,,-/)]—г-—
4 эЬ (х,/)
Выражения (7), (8) позволяют определить импеданс проводника
••
£(о))*=£7//, где И=Ьг ^]|£, — разность потенциалов, приложенная
«•*—<»
К проводнику, £* — его длина.
Действительная часть частоты желобковых колебаний в лабораторной системе отсчета отлична от нуля (ф^О). Поэтому составляющие импеданса, пропорциональные ехр(:Ыф), после усреднения по времени обращаются в нуль. В результате получаем
|
I(x)Ls У* Sh(x«(Z—A) )sh(x, a) |
![]() (м. а
(м. а
(9)
LyC2 Х, Sh (X,Z)
О»
62 — ~7~Tr 5И(~Т7^7Г) (».,+ Cth (х.,+0 +х,,_ Cth (х, _I)). (10)
Ic LVВЪМ)'
Предположим, что ВЧ поле поддерживается колебательным контуром, частью которого является рассматриваемый проводник. Добротность контура будем полагать достаточно высокой, так что декремент затухания ВЧ колебаний намного меньше характерной частоты желобковых колебаний. В этом случае при анализе взаимодействия ВЧ и НЧ колебаний система может считаться консервативной. ВЧ энергия, запасенная в контуре, дает-
|
Рис. 1 |
|
Рис. 2 |
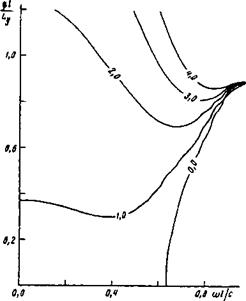
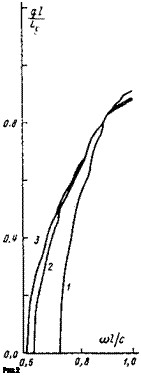 Рис. 1. Линин уровня величины Г на плоскости переменных (й>//с, ЯУЬу) при а//=0,5
Рис. 1. Линин уровня величины Г на плоскости переменных (й>//с, ЯУЬу) при а//=0,5
Рис. 2. Положение линии уровня Г=-0, ограничивающей область параметров, в которой возможна стабилизация, при различном положении антенны: 1 — а//=0,75, 2 —
А//=0,5, 3 - А11=0,25
Ся выражением (см., например, [8))
Где Ъ! — полный импеданс всей цепи, включая ВЧ антенну.
Частота собственных колебаний контура определяется условием 2/(о))=0, из которого находим изменение частоты при возникновении же - лобковых колебаний. Учитывая также условие постоянства адиабатического инварианта, определяем изменение энергии в контуре
|
6И^ = |
(I)
Условие стабилизации желобковой неустойчивости имеет вид
162Г1 /2 Агр0
Будем считать д^1, Ьу&(1—а). В этом случае основной вклад в суммы по 5 в (9), (10) дают слагаемые с |$|<£„/(/—а), и выражение для |б2| удобно представить в виде
Огй)£,Г * * 4я Сг(1-ау'
Где величина Г довольно слабо зависит от параметров а//, <о//с, д, ЦЬЧ (рис. 1, 2). Максимальная величина ВЧ магнитного поля на поверхности плазмы В~ связана с током соотношением 1~с(1—а)В„. Учитывая эти оценки, приводим условие стабилизации к виду
Если данный критерий использовать для реальных аксиально-симметричных систем, то Ьу/п следует заменить на радиус системы — характерный масштаб изменения переменного магнитного поля в отсутствие плазмы. При этом условие устойчивости означает, что градиент ВЧ давления превышает «выталкивающую силу», действующую на плазму в неоднородном магнитном поле. Обычно радиус системы мал по сравнению с характерным масштабом изменения магнитного поля, поэтому и ВЧ давление, необходимое для стабилизации, оказывается малым по сравнению с давлением плазмы., Это обстоятельство позволяет не учитывать влияние ВЧ поля на равновесное состояние плазмы.
Наиболее существенным эффектом, обусловленным аксиальной симметрией реальных систем, является возможность раскачки так называемой первой моды желобковых колебаний. Этой моде отвечает жесткое смещение плазменного шнура без деформации его поверхности. При описании воздействия ВЧ поля на первую моду усреднение по фазе <р оказывается неправомерным. Действительно, можно подумать, что к усреднению должно приводить вращение плазмы в самосогласованном электрическом поле. Однако ось вращения совпадает с осью плазменного шнура. Поскольку она смещается вместе с шнуром, то вращение не изменяет значения фазы <р. В результате влияние*ВЧ поля на устойчивость будет определяться эффектами первого порядка по смещению а, причем знак радиальной силы, действующей на смещенный шнур, зависит от значения фазы <р. Для того чтобы при всех значениях ф получить силу, возвращающую шнур, необходимо, как и в случае постоянного тока, использовать достаточно большое количество проводников (палки Иоффе).
3. Взаимодействие желобковых колебаний с поверхностными модами
Рассмотрим непотенциальные поверхностные моды с частотой порядка ионной циклотронной ах. Как следует из [ 9], уравнение, описывающее такие колебания, можно представить в виде
Здесь В=В(х, Y)exJ)(—шt+iN]]z) — г-компонента возмущенного магнитного поля, Ь=В0/£0, ^=(е-А^112)//), /)=(е-^,2)2-^, е=1+соР<7
/(о)<2—<о2), G=(дp^г(д|(Oi((й^г—(i)г), координаты х, У, г обезразмерены посредством множителя о>/с. Как и выше, будем считать, что в отсутствие желобковых колебаний плазма имеет резкую границу и занимает область х<0. Воздействие желобковых колебаний приводит к гофрировке границы плазмы по закону х=азт(ду). Считая амплитуду гофрировки малой по сравнению с характерным масштабом изменения возмущенного магнитного поля, выражение для В(х, У) выберем в виде
В(хуу) = (В(0) (х) +а(Я(1>+(х)е^+В{ 1)~ (х) е~^) + +а ГВ{г)(х))ешуу.
![]()
|
В нулевом приближении по параметру А имеем |
![]() Функции В{к) (х) (&=0, 1, 2) различны по разные стороны от границы плазмы. Их сшивка осуществляется с помощью условий, имеющих смысл условий непрерывности г-компоненты возмущенного магнитного поля и тангенциальной составляющей электрического поля
Функции В{к) (х) (&=0, 1, 2) различны по разные стороны от границы плазмы. Их сшивка осуществляется с помощью условий, имеющих смысл условий непрерывности г-компоненты возмущенного магнитного поля и тангенциальной составляющей электрического поля
Условия сшивки дают
ВГ.-вр =я<0),
В"»=хех&ех+*ы&ы+и#=0.
Последнее соотношение является дисперсионным, определяющим зависимость частоты поверхностных мод от Л’ц. В предельном случае
Му^&ех'хп дисперсионное соотношение принимает простой вид
Е—2Л^,2=0.
13 следующем (первом) приближении по малому параметру А получаем
(1) + 1*а ±д(^е*-^<п)+х, я(ч^в-х1я±)^,,п+х<?,(хе,±-х, х)^,«
О« ==Ь—1-х« +
2 I ** $ (МУ±д)+&^Кхп±+&'хН>'
(1)± ,1а, ,
В%п =±.—Кы+Кех)+Вех .
9
Выкладки второго приближения по А чрезвычайно громоздки. Однако оказывается, что в предельном случае Ny'>q|Ly дисперсионное соотношение, учитывающее поправки на гофрировку, может быть представлено в компактном виде
0=0'°' - — + —) = 0.
2 'хех х, п'
При выполнении условия Nyг^>&,x'in поправка к частоте, обусловленная влиянием гофрировки границы, дается выражением
Ба) _ /«д2#||2 со+о),
О) 'Ny' 2 а)+2А),
Как и в предыдущих разделах, будем считать, что частота поверхностных колебаний значительно превышает частоту желобковых колебаний. Следовательно, при эволюции последних должен сохраняться адиабатический инвариант 1¥/<о, где IV — энергия поверхностных колебаний (см. Приложение 2). В силу этого соотношения отрицательный знак ба) (см. (11)) свидетельствует о дестабилизирующем воздействии поверхностных колебаний на желобковые.
Авторы благодарны Д. Д. Рютову за обсуждение работы.
ПРИЛОЖЕНИЕ 1
Энергия желобковых колебаний. Рассчитаем изменение энергии плазмы, вызванное смещением ее границы в возмущениях жедобкового типа. Будем считать, что давление плазмы Р0 мало по сравнению с давлением магнитного поля, и соответственно рассмотрим потенциальные колебания. Изменение энергии плазмы при ее смещениях дается следующим выражением:
= — [ *(*У)р0йпг*, (П1.1)
2
Где £—(/с/Во2) [В0УФ], ф — электрический потенциал. Учитывая соотношение
= - В0-1{ЪЧ)Во, преобразуем (П1.1) к виду
— *г-1-(^)Во(^)ро.
2 Во
Если давление плазмы постоянно при х<0, то изменение энергии, приходящееся на единицу площади поверхности плазмы, дается выражением
1 ЙВ0 I
=------------------------------------- РоА2, (П1.2)
2В0 йх I х„о
Где А — амплитуда смещения границы.
Энергия поверхностных мод. Энергию поверхностных мод можно рассчитать, вычислив, например, работу внешней силы, затрачиваемую на их возбуждение. Коде - банж плазмы, плотность которой зависит только от координаты х, описываются уравнением [9]
|
[ |
D D / to П 4л 1
— # NJ8+X У$х'+ ( — ) В rotz/y, cT» (П2.1)
Dx Dx У V с / J С iV^-1
Где /*, ст — у-компонента плотности стороннего тока, В — z-компонента магнитного поля колебаний.
Помножив уравнение (П2.1) на В* и произведя ряд простых преобразований, получаем
DxjyEv = — ) l*lXV
4ло) с / /
Здесь учтено соотношение (—ic/a>) (1—NV2)-XBX W — «погонная» плотность энер
Гии. Заменяя в последнем выражении ш на Ы+Idldt и отделяя действительную часть, подучаем
W~~R ) (1в>'12+лг»21«12)+л'Х.|в|2+4-1в1;1У