О НЕУСТОЙЧИВОСТИ МАГНИТОЗВУКОВЫХ КОЛЕБАНИЙ В ОТКРЫТЫХ ЛОВУШКАХ
ЗВОНКОВ А. В., ТИМОФЕЕВ А. В.
1. Неустойчивости с частотами порядка ионной циклотронной, развивающиеся в открытых ловушках, разделяются на «конусные» и «анизотропные» Первые вызываются немонотонностью функции распределения по Г± — энергии движения в направлении поперек магнитного поля. Как оказалось, такие неустойчивости можно эффективно подавлять введением небольшой добавки холодных ионов. В этих условиях на первый план выступают анизотропные неустойчивости, обусловленные превышением средней энергии поперечного движения над средней энергией продольного. Из них наиболее опасной считается неустойчивость альфвеновских колебаний, наблюдавшаяся в экспериментах на установке ТМХ [1]. Теоретическому исследованию этой неустойчивости посвящена обширная литература (см., например, [2]). Однако, как известно, частота альфвеновских колебании не может превысить ионную циклотронную частоту, между тем в [1] наблюдались и колебания на гармониках ионной циклотронной частоты й)/<1)»«2, 3, 4. Эти колебания, как и колебания с ю«©*, являлись непотенциальными [1] и поэтому их естественно отнести к магнитозвуковым. В настоящей работе рассчитывается инкремент магнитозвуковой неустойчивости в плазме открытых ловушек. Обсуждается возможность е& стабилизации запробочной плазмой. В амбиполярных открытых ловушках магнитозвуковые колебания могут раскачиваться в крайних ловушках,, а роль запробочной играет плазма центральной ловушки, обладающая равновесным распределением по скоростям.
2. ![]()
|
Л**,1- (^г + 4 ^*) (е+++е—) +е++е—=0. (1) |
![]()
|
(1) |
![]()
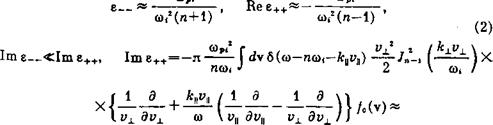
|
Й),12 |
![]()
|
Й)Р12 |
![]()
|
Вают отклик плазмы на поперечное электрическое поле, вращающееся соответственно в ионную (Е+=Ех+1Еу) и электронную (Е-=ЕХ—1ЕУ) сторону. Использование этих сочетаний вместо декартовых компонент позволяет записать дисперсионное уравнение в более компактном Ц удобном для. дальнейшего исследования виде. При ©«шо,, К±Р<<1 имеем |
 Дисперсионное уравнение магнитозвуковых колебаний в однородной члазме имеет вид
Дисперсионное уравнение магнитозвуковых колебаний в однородной члазме имеет вид
Вхр(-П(Д-1))Х 2А (Д) (я!)2 4(п+1) / ^ П "
Х{^(?^Гмад^“л('*»-ч'И-
Здесь обозначено й)р» — плазменная частота, <о» — ионная циклотронная частота, д,= (й)р»/й)»)2, р, — Ионный Ларморовский радиус, /п — функция
К
Бесселя индекса «л», б^агс^ —, предполагается, что 0<1 см. ниже,
|
Где 1пД |
![]() Значки «перпендикулярно» и «параллельно» отмечают направление по отношению к магнитному полю. Функция распределения ионов по скоростям выбирается в виде [3]
Значки «перпендикулярно» и «параллельно» отмечают направление по отношению к магнитному полю. Функция распределения ионов по скоростям выбирается в виде [3]
|
■4-ЧД), ,4 (Я) |
V -1/0-1/04 ' О /
2 л *ит3 УЛ_УЛ_1 г Д
Д — пробочное отношение, которое мы будем считать в достаточной степени отличающимся от единицы (Д—1^1). Выбранная функция хорошо описывает распределение ионов по скоростям, устанавливающееся в открытых ловушках под действием кулоновских столкновений. Остальные обозначения следующие:
1 / <о—я©» 2 /27,1/г, / , Йп~1 1
Ч“д=Г• 1;т=(_^7/ ’ ^=(-1}
^1 (л)= Йч — Е-
: л
Из (1), (2) Находим инкремент колебаний. Если £Д<1 (£=8лПТ/Вг),
/ П+1 ч1/»/ В 4 • то он максимален при 0=0m;5^З,/, ^^ ^ Д(Д—1)/ И Равен
TOC o "1-5" h z _ ,/ 3 *+! пг”-"/Чл+1)5‘/* (л-1)3 „
Ттах СО {Я (-------------------------------------------------------------------------------- I < В '* X
4е / (п!)2(2+(п+1)(л2-2)) Р
V______ 1_____ Г / 1»‘(|»+1)Я(Д-1) *1 ...
Д“+,Л(Д-1)'М(Д) ехр1 р ) ]‘ *
Г> , л /„ д-1 ‘л 1 , ,/п*(га+1)
При |Ш>1 имеем 6т » ) _1п-(^-1Г) я
В ___________________ (гс-1)3_____________
|
(4) |
![]() 'т“~ е"+1 (га+1) П~‘/,пп‘ (2+ (ге+1) (ге2-2))
'т“~ е"+1 (га+1) П~‘/,пп‘ (2+ (ге+1) (ге2-2))
В неоднородном магнитном поле открытых ловушек анизотропные неустойчивости имеют частоту й)~гсй)»га1п [4]. Они раскачиваются в пределах резонансной зоны, расположенной в окрестности минимума магнитного поля. Ее размер определяется эффектом Допплера и по порядку величины равен 1л~Ьь(№т/(иУ'. Здесь Ь0 — характерный масштаб изменения магнитного поля в центре ловушки, где 2?(2)«2?о(1+(2/£о)*), координата 2 отсчитывается вдоль магнитного поля. Неоднородность магнитного поля при-
Т ~ Ь° / Р
L — размер системы, ^о^Ттах-Г - I --- 7 ) .
L гс+1/
При Я<l «грубая» зависимость инкремента от частоты и волнового вектора определяется экспоненциальным фактором^~<о»ехр^ — ^—-——^ J.
Поскольку при этом мал как инкремент колебаний ('у/ю^ехр (—l/Я))r
Так и характерный масштаб его изменения в функции от волнового векто-
/ I CО In Y / cf ln СО I 1 ^
Pa I —-— / —------------ ~ — ), то неустойчивость должна быть сносо-
Вой (см., например, [5] ). Влияние на нее запробочной плазмы будем характеризовать величиной
<Im8++> == — J dzlme++(z), где Ime++(z)
Определяется (2) с максвелловской функцией распределения. При Я<l и линейном профиле магнитного поля в окрестности резонансной точки
(В0(z) =В0 ^ 1 + j » n<ыi(z,)—<o) получаем следующие выражения
Для вклада запробочной плазмы в инкремент:
3"+1Л (N-l)3n(in-8)/3
1.* 22n+3 „,(П+1)<П-.„/З(2+(Ге+1)(Га2_2))
Li
При Я/?<l И
. _Я______________ (га-1)3_____________ х
ТГ.» ®I(z.) 22n+3 п! п4(п+1)п-5(2+(га+1) (ге2_2))
*(^Т............................
При рД>1.
Из выражений (5), (6) следует, что стабилизирующее воздействие запробочной плазмы возрастает с увеличением давления плазмы и уменьшением градиента магнитного поля (ср. с [6]). Для достаточно больших значений Li и Я. t суммарный инкремент 'fo+'fi может оказаться отрицательным, что будет означать стабилизацию колебаний.
В заключение отметим, что магнитозвуковые колебания, как и альфве - новские, могут раскачиваться и на основной гармонике ионной циклотронной частоты (со«©»), однако при Я<l их инкремент мал по сравнению с инкрементом раскачки альфвеновских колебаний
Q{ sin4 0 1