ФИЗИКА ПЛАЗМЫ

О НЕУСТОЙЧИВОСТИ КОЛЕБАНИЙ С ЧАСТОТОЙ, РАВНОЙ ПОЛОВИНЕ ОТ ИОННОЙ ЦИКЛОТРОННОЙ

А. В.Тимофеев

1. Известно, что в адиабатических ловушках плазма может быть неустойчивой по отношение к раскачке ионных циклотронных колебаний, т. е. колебаний, частота которых близка к ионной циклотронной или

К ее гармоникам п<а, • Однако, в экспериментах на установках Феникс []] и Огра-1 (не опубликовано) наряду с ионной циклотронной неустойчи­востью наблюдалась раскачка колебаний с частотами, кратными полови­не ионной циклотронной частоты ш - -2- <а, . По нашему мнению, воз-

2

Буждение колебаний последнего типа может быть связано с явлением параметрического резонанса. Поясним это утверждение. Ионная циклот­ронная неустойчивость начинает раскачиваться при такой плотности плазмы, когда частота замагниченных электронных ленгмюровских ко­лебаний сравнивается с ионной циклотронной [2,3]. В однородной и безграничной плазме спектр частот замагничеш^лх электронных ленг - мюровских колебаний дается формулой ы - ыпл ^ & .здесь <а_ -

Р9 £

Электронная ленгмюровская частота, кн - компонента волнового векто­ра вдоль магнитного поля. В ограниченных системах спектр дискретен и для раскачки необходимо, чтобы максимальная частота из этого спект­ра сравнялась с а>{. (Эта частота меньше <ар# , так как раскачиваются

Колебания с к±± 0). При этом колебания с меньшими частотами в рамках линейной теории остаются устойчивыми. Однако, при наличии неустойчи­вости на ионной циклотронной частоте параметры плазмы становятся переменными во времени, и это^создает предпосылку для параметричес­кой раскачки колебаний с - - у* . При существенно больших значе­

Ниях плотности шр#> пш/ становится возможной параметрическая рас­качка колебаний с о - ( / = 1,2,... 2п)

2. Предположим, что в адиабатической ловущке возбуждены колеба­ния электрического потенциала на ионной циклотронной частоте. Интере­сующие нас системы (Феникс, Огра-1) обладают аксиальной симметрией (ось симметрии параллельна магнитному полю Н || 07 ). Поэтому воз­мущения потенциале будут иметь вид фх( т,*) = фг(г, ж )с оз(&^ - ъгв)9 здесь в - азимутальный угол. При рассмотрении эволюции колебаний

С ал - у - *>i будем использовать асимптотические методы, развитые е

Теории нелинейного осциллятора [4]. В ряде случаев эти методы приме­нялись и в теории плазменных колебаний [5,61. Следуя [4-61,будем ис­кать возмущения потенциала в виде ф2(г, О = ф2(г, х^)соб/2 +

+ ) - т2$) дальнейшем будет педполагать, что характерный временной

Масштаб амплитуды фг(г, х,г )9 а также медленно меняющейся части фа­зы фО) велик по сравнению с циклотронным периодом.

Временная зависимость ф2 (г, х^) и ф^) должна определяться с помощью уравнения движения электронов, уравнения непрерывности и уравнения Пуассона. Произведя несложные выкладки получаем :

Ф=Ъы - Ас оь2ф, (1) р - - р A sin 2 ф k (2)

Здесь р * [ < (<9 ф2 / дх )2 > ]х/2 , 8 со - б>2 - /2, й> 2- - частота

Рассматриваемых колебаний в линейном приближении, т. е. при * 0.

По - невозмущенная плотность

Плазмы, скобки означают интегрирование по г и z.

Интересно отметить, что точно такие же уравнения для p(t), ф(t) получаются из уравнения Матье :

(3)

Если решение (3) искать в виде х = p(t) cos

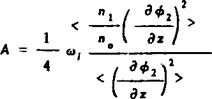Эта аналогия позволяет перевести результаты исследования (3) на наш случай. В частности, если частота собственных колебаний <а2 окажется близкой б>/ /2, то рассматриваемые колебания будут неустойчивыми. Условие раскачки имеет вид :

> | S <u| - | <и2 - ---------- | _ (4)

2

При этом для раскачки также оказывается необходимым, чтобы вместе с частотой делилось и азимутальное волновое число т, т. е. имело мес­то соотношение т2 = ту/2.

Для того чтобы проверить, выполняется ли условие (4) в реальных системах, требуется точное решение задачи о собственных колебаниях плазмы в линейном приближении с определением вида функции п ^г, г), ф2(г ,х)9 а также частоты собственных колебаний й>2. Для этого в свою очередь необходимо знание невозмущенного распределения плотности плазмы п0(г, х). Однако, соответствующие экспериментальные данные отсутствуют. Поэтому, строго говоря, наше утверждение о параметри­ческом характере раскачки колебаний с ш - <и, /2 остается лишь гипо­тезой. В его пользу свидетельствуют измерения азимутальной зависи­мости возмущений [ Ц. Из результатов этих измерений можно сделать вывод о том, что колебания с о * «а,/2 обладали вдвое меньшим ампли­тудным волновым числом, чем колебания с о » <и/ , как это и следует из теории. Соответствующие измерения на Огре - 1 не производились.

В этих экспериментах при плотности, существенно большей критической, наблюдалось возбуждение колебаний с ш - п<и,/2 (7 > п > 2). Их

Раскачку естественно связать с возбуждением высших резонансов,

См. [4].

В заключение заметим, что параметрическая раскачка колебаний может рассматриваться, как частный случай распадной неустойчивости. Условие распада колебания с частотой ш на два колебания с частота­ми <и1 и <о2, как известно, имеет вид ш - ы1+ . При параметричес

Ком резонансе имеем <и1 - <и2 - со/2. С другой стороны в [в] показано, что в определенном смысле сама распадная неустойчивость эквивалент­на параметрическому резонансу. В частности, подходящим выбором пе­ременных уравнения, описывающие распадную неустойчивость, могут быть приведены к виду (1), (2). Так например, если в однородной и безг­раничной плазме замагниченные ленгмюровские колебания с частотой ш и волновым вектором к ф(т^) = ^ со в (кг - шО распадаются на два других 6(1’2)(г, О - Ф{1*2)(*)соб (кх 2г - ^ *

То в этом случае в уравнениях (1), (2) следует положить

П = -~2а,6 ,

Поступила в редакцию 1« августа 1969 г.