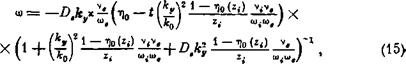НИЗКОЧАСТОТНЫЕ ДРЕЙФОВЫЕ КОЛЕБАНИЯ СЛАБОИОНИЗИРОВАННОЙ ПЛАЗМЫ
С. В. Пу те икс кий и А. В. Тимофеев
Показано, что в бестоковом газовом разряде при неполной замагниченностя ионов (<•>,-/*,• —'1, р,/а —1/гт-1/з) могут самопроизвольно возбуждаться низкочастотные (о) дрейфовые колебания. Здесь — ионная циклотронная частота, — частота ион-нейтральных соударений, ш — частота колебаний, р,- — ионный лармо - ровский радиус, а — характерный масштаб изменения плотности плазмы. Сопоставление теоретических и экспериментальных результатов свидетельствует в пользу того, что эти колебания наблюдались в экспериментах [1. *]. Показано, что в сильных магнитных полях (о></ 1, р{/а<^1) остаточные эффекты неполной з а магничен -
Ности ионов оказывают стабилизирующее воздействие на дрейфовые колебания.
Введение
При исследовании высокочастотного газового разряда в магнитном поле было обнаружено, что в некотором довольно узком интервале значений магнитного поля в разряде самопроизвольно возбуждаются колебания, частота которых с ростом магнитного поля меняется немонотонно, образуя характерный клювик I1’ *]. Абсолютное значение частоты колебаний может быть малым по сравнению с частотой ион-нейтральных соударений, и поэтому возбуждение колебаний нельзя объяснить действием дрейфово-диссипативного механизма раскачки [3]. К возбуждению низкочастотных колебаний может приводить механизм, рассмотренный в [4]. Он действует, если плазма по отношению к стенкам разрядной камеры заряжена отрицательно, а радиальное электрическое поле, вызываемое этим зарядом, достаточно велико. Авторы работ [*» 2] использовали результаты теории, развитой в [4], для объяснения колебаний с растущей зависимостью частоты от магнитного поля. Однако падающая ветка колебаний может раскачиваться даже при положительном заряде плазмы.
В условиях экспериментов I1* 2] из-за сравнительно большой плотности заряженных частиц не мог проявиться и механизм, связанный с нарушением квазинейтральности плазмы [5].
Теоретическая модель явления, предлагаемая нами, основана на учете некоторых особенностей, характеризующих неустойчивое состояние плазмы. В экспериментах I1' *] наиболее существенной из них, по нашему мнению, является неполная замагниченность ионного компонента слабо - ионизированной плазмы газового разряда, а именно в неустойчивом режиме ионная циклотронная частота ш,. близка к частоте ион-нейтраль - ных соударений а ларморовский радиус ионов составляет значительную долю, порядка 1/а-г1/, от радиуса разрядной трубки а. При этих условиях скорость дрейфа ионов в скрещенных полях (электрическом поле колебаний и постоянном магнитном) должна существенно отличаться от скоростей дрейфа электронов. Согласно [*] различие в скоростях дрейфа может привести к раскачке низкочастотных дрейфовых колебаний неоднородной плазмы.
Анализ поведения плазмы с большим ларморовским радиусом ионов представляет значительные математические трудности. Для упрощения
Вычислений мы использовали разложение по параметру р^/а, считая лар - моровский радиус ионов малым. При р^/а — 1/2-г178 результаты, полученные нами, не могут претендовать на большую точность и имеют в значительной степени лишь иллюстративный характер. Поэтому мы особое внимание обратили на интерпретацию качественных закономерностей, наблюдавшихся на эксперименте, характера зависимости частоты колебаний от магнитного поля, зависимости критического магнитного поля от давления и т. д.
Поведение ионного компонента плазмы описывалось кинетическим уравнением с интегралом столкновений в форме Батнагара—Гросса— Крука. Как известно, такой интеграл столкновений хорошо работает в случае слабоионизированной плазмы, где преобладают столкновения с нейтральными частицами. Использование кинетики вызвано необходимостью учета эффектов конечного ларморовского радиуса. Если бы плазма была полностью ионизированной, то эффекты конечного ларморовского радиуса можно было учесть в гидродинамике через вязкость. Однако в слабоионизированной плазме обычная гидродинамика непригодна [7]. Действительно, при выводе гидродинамических уравнений предполагается, что столкновения не меняют полного импульса и энергии, в то время как при столкновениях с нейтралами ни импульс, ни энергия заряженных частиц не сохраняются. Формальное использование гидродинамики в интересующем нас случае приводит к ошибочным результатам. (Поправки на эффекты конечного ларморовского радиуса имеют неверный знак).
1. Основные уравнения. Начальное состояние
Поведение ионного компонента слабоионизированной плазмы будем описывать кинетическим уравнением
Здесь столкновительный член взят в форме, которая учитывает сохранение числа ионов при столкновениях с нейтральными атомами
|
(2) |
![]()
|
Где v< — частота ион-нейтральных соударений, |
![]() 81 (/) = —V, (/ - /.„) + »,£$(/-/*) *у.
81 (/) = —V, (/ - /.„) + »,£$(/-/*) *у.
|
|
Т. — температура нейтрального газа. Предполагается, что при столкновениях ионы приходят в тепловое равновесие с нейтралами.
Разрядные трубки аксиально-симметричны, причем в отсутствие колебаний градиент плотности и электрическое поле направлены по радиусу. Для упрощения задачи введем эквивалентную систему с плоской симметрией, в которой направление вдоль ОХ эквивалентно радиальному и вдоль 02— азимутальному. Ось ОЪ направим вдоль магнитного поля. Решая (1) в предположениях
|
|
|
|
,/ЦоЄТо, 1 Я; , 1 «То. I ** + 01
"*ЧП„ Т, Т 2 2 Т, ■+■ 2 V Ті ) ) ш} + V}
|
|
Из членов второго порядка малости в разложении (3) учтены лишь те, которые дают вклад в плотность.[34] Скорость определяется первым членом разложения
= (4)
Здесь Ь( = е/т^( — коэффициент подвижности ионов; — коэффициент диффузии; б>а=ь.(у2/ш54-у|); ь,.,=(®4/у^«А; ММ+'’!);
°й = ви»(/,с
Обычно предполагается, что даже при наличии столкновений невозму - щенное состояние плазмы можно описать функцией от интегралов движения и[35], x-{-vv|iйi. В настоящем случае такой подход привел бы к неверным
Выражениям для ионной скорости.
В силу того что ларморовский радиус электронов мал, их движение можно описывать с помощью уравнения неразрывности
TOC o "1-5" h z -£ + <«у(пУ,) = 0 (6)
И уравнения баланса импульса
0=— г,7п+ етЯч—^.[УН] — т. пУ. у,. (7)
Здесь предполагается, что выполнено условие квазинейтральности пв =
= 7^ = п и что температура (средняя энергия) электронов в колебаниях
Не меняется. С помощью (7) можно найти выражения для компонентов начальной скорости электронов, которые будут отличаться от (4), (5) лишь знаком перед коэффициентом подвижности и индексом
В диэлектрических разрядных трубках скорости движения электронов и ионов на стенки трубки должны быть равны. Из этого условия определяется амбиполярное электрическое поле
Р __ *о
°~ + «О “
2. Низкочастотные дрейфовые колебания
При исследовании дрейфовых колебаний обычно используется так называемое локальное квазнклассическое приближение, а именно малые возмущения электрического потенциала, функции распределения ионов и плотности выбираются в виде плоских волн, бегущих в плоскости, перпецди - кулярной ОХ, х = л^/л0~ а“1.
Рассмотрим колебания с к9 кж, Электроны будем считать
Замагниченными а начальное электрическое поле слабым
1. Здесь и = (с/Н) (^йро/Аг), условия хр,1, |*и/а>,| 1 позволяют учесть
Лишь два первых слагаемых в выражении для /0. Рассматривая движение электронов и ионов в поле колебаний, получаем следующие соотношения
Между возмущениями плотности и потенциала (напомним, что плазма считается квазинейтральной):
+
|
(9) |
А, р, 8 — поправки, связанные с учетом конечного ларморовского радиуса ионов
00
|
*1« (О *1 V} + п 2*2 |
|
К)+2 2 |
|
По |
|
*=1 |
|
В = 1 — |
|
+ п2ц,2)2 Ъ <*,)»• 0-5+ »|) |
|
11=1 00 |
|
. , А!, _1 У-МпгМ + г% А + Я2«? = -1 +----------------------------- гг5---------------------- |
|
, «V11« (*■) «**ы £ Н + п |
|
1^)2 |
|
11=1 |
|
, V Ун (*<) д^Н А М + Л*«|)2 |
|
*=1 |
|
|
|
|
 |
В выражениях для поправок (10) использованы следующие обозначения: 2<=А? р5; р, = (»71 (Т41т4)Ч* — ларморовский радиус ионов; 1я(г^ — функция Бесселя мнимого аргумента; т|ж (з,) = 1п (г,) егж*. Дисперсионное уравнение получаем, приравнивая определитель системы (9) нулю. Из дисперсионного уравнения находим частоту колебаний на границе неустойчивости (1т о) = 0)
Х(1—<1 -»£ (%)’^)(<+«<'•>
И условие раскачки колебаний
Дл0;+£)<—«“О +а^)^7(1_?г,+ш^7(а+8)(1~рг1- (12)
В (И) и (12) обозначено: А| = Щ + к* (*#/а>#)2.
В работе [*] показано, что частота неустойчивых дрейфовых колебаний слабоионизнрованной плазмы должна быть больше частоты столкновений ионов с нейтральными атомами <*> > V,. Однако из (11) следует, что если плазма по отношению к стенкам заряжена положительно хи > О, то частота неустойчивых колебаний может даже обратиться в нуль. При этом условие неустойчивости (12) будет выполнено, если поправки на эф-
2088
Фекты конечного ларморовского радиуса (а, 8) во втором слагаемом в правой части (12) достаточно велики. Заметим, что механизм неустойчивости, рассмотренный в [4], действует при обратном знаке электрического поля (хи < 0), когда в правой части (12) преобладает первое слагаемое.
|
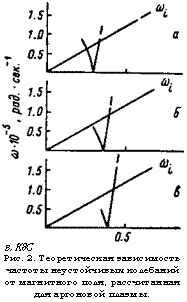
В, К8С Рис. 2. Теоретическая зависимость частоты неустойчивых колебаний от магнитного поля, рассчитанная для аргоновой плазмы. |
|
А| соответствует соленоиду Ь — 60 см. а — р = 5 • 10~3, б—8 • 10~3, в— 1 • 10~* тор. |
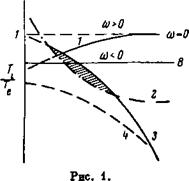
![]() Эти соображения проиллюстрированы рис. 1. Область неустойчивости располагается под кривой 3. С увеличением магнитного поля (уменьшением ларморовского радиуса) эта кривая переходит в кривую 4. Последняя дает критическое поле для неустойчивости, рассмотренной в [4]. Типичная для обсужденных экспериментов зависимость электрического поля от магнитного дается кривой 2. Область неустойчивости расположена между кривыми
Эти соображения проиллюстрированы рис. 1. Область неустойчивости располагается под кривой 3. С увеличением магнитного поля (уменьшением ларморовского радиуса) эта кривая переходит в кривую 4. Последняя дает критическое поле для неустойчивости, рассмотренной в [4]. Типичная для обсужденных экспериментов зависимость электрического поля от магнитного дается кривой 2. Область неустойчивости расположена между кривыми
|
ЛЕ. ХТт
1 — электрическое поле, при котором О>=0. Частота (фазовая скорость) положительна над кривой; 2 — характер - ная экспериментальная зависимость электрического поля от магнитного; 3 — критическое электрическое поле. Колебания неустойчивы при Е < Е, 4 — критическое поле, полученное |
2 Я 3 (заштриховано). На кривой 1 обращается в нуль частота колебаний (фазовая скорость). Выше ее расположена область, в которой колебания имеют положительную фазовую скорость, т. е. вращаются в электронную сторону (падающая ветка).
3. Численные расчеты. Сопоставление с экспериментом
|
ЕЕ о |
![]() Из уравнения (9) с учетом поправок (10) были получены выражения для частоты колебаний а> и инкремента у. Ввиду того что эти выражения оказались достаточно громоздкими, были проведены численные расчеты зависимости частоты неустойчивых колебаний от магнитного поля. Для того чтобы сравнить полученные результаты с экспериментом, значения параметров, входящих в дисперсионное уравнение, выбирались в соответствии с работой [2], в которой наиболее полно представлены экспериментальные данные. При расчетах мы использовали экспериментальные значения стационарного электрического поля. Заметим, что оно отличается от амбиполярного поля (8), превышая его примерно на порядок величины. В таком поле ионы между столкновениями с нейтралами могут набирать довольно значительную энергию, существенно превышающую тепловую энергию нейтралов. Эффективная ионная температура вычислялась по формуле
Из уравнения (9) с учетом поправок (10) были получены выражения для частоты колебаний а> и инкремента у. Ввиду того что эти выражения оказались достаточно громоздкими, были проведены численные расчеты зависимости частоты неустойчивых колебаний от магнитного поля. Для того чтобы сравнить полученные результаты с экспериментом, значения параметров, входящих в дисперсионное уравнение, выбирались в соответствии с работой [2], в которой наиболее полно представлены экспериментальные данные. При расчетах мы использовали экспериментальные значения стационарного электрического поля. Заметим, что оно отличается от амбиполярного поля (8), превышая его примерно на порядок величины. В таком поле ионы между столкновениями с нейтралами могут набирать довольно значительную энергию, существенно превышающую тепловую энергию нейтралов. Эффективная ионная температура вычислялась по формуле
— Го
Здесь Т0 — температура нейтралов: р,. — длина свободного пробега
И ларморовский радиус ионов. Температура электронов Тв в [*] была
равна 4 эв. Значение х ^ —2 см“1 определялось из экспериментального распределения начальной концентрации п0. Поскольку мы решали не цилиндрическую, а плоскую задачу, то первая азимутальная мода отождествлялась с колебаниями с волновым числом &у=|*|. Второй моде соответствовало ку=2|х|, и т. д.
Колебания, наблюдавшиеся на эксперименте, представляли собой основную моду в продольном направлении, а именно вдоль оси трубки укладывалась половина длины волны. Длина разрядной трубки превышала длину используемых соленоидов, поэтому длина плазмы в направлении вдоль магнитного поля примерно равнялась длине соленоида. В силу этого при длине соленоида, равной 20, 40 и 60 см, продольное волновое число было равно соответственно 0.156, 0.104 и 0.052 см-1.
|
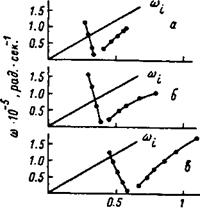
Р. ггс Рис. 4. Экспериментальная зависимость частоты низкочастотных колебаний в аргоновой плазме от магнитного поля в соленоиде £=60 см. |
|
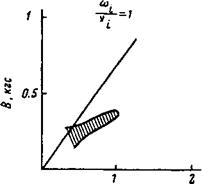
Рис. 3. Расчетные границы неустойчивости падающей по частоте ветви низкочастотных колебании. |
![]()
|
Р'Ю, тор |
![]() К■ соответствует соленоиду I, = 60 см.
К■ соответствует соленоиду I, = 60 см.
|
В — Р: |
![]() •8.10-*, 6 — 1.10-», — 1.5-10“* тор.
•8.10-*, 6 — 1.10-», — 1.5-10“* тор.
На рис. 2 изображена полученная зависимость частоты неустойчивости колебаний от магнитного поля для различных давлений, на рис. 3 — область неустойчивости по давлению и магнитному полю для падающей ветви колебаний. На рис. 4,5 приведены результаты экспериментов [2]. Для сравнения теории с экспериментом на рис. 3,5 мы выделили колебания с падающей зависимостью частоты от магнитного поля по двум причинам: во-первых, такие колебания существуют в довольно узкой области параметров, во-вторых, именно в этих колебаниях эффекты неполной замагни- ченности ионов, в частности эффекты конечного ларморовского радиуса, проявляются в наиболее чистом виде. Что касается колебаний с растущей частотой, то при отрицательном электрическом поле достаточно большой величины они могут раскачиваться, даже если ларморовский радиус ионов равен нулю [4]. (На рис. 1 кривые 3 и 4 с ростом |£| сближаются). Зависимость частоты неустойчивых колебаний, полученная теоретически, имеет то* же вид, что и наблюдавшаяся на эксперименте. Однако вся картина сдвинута в сторону меньших значений магнитного поля. Это расхождение естественно связать с упрощенным характером использованной теоретической модели. Заметим, что хотя абсолютные значения магнитного ‘поля и давления в рассчитанной области неустойчивости отличаются от экспериментальных, по безразмерному параметру имеется хорошее
Соответствие. Близость этой величины к единице понятна, поскольку в этом случае ионы в достаточной степени замагничены, что необходимо для существования дрейфовых колебаний, и в то же время максимальна разность скоростей дрейфа в скрещенных полях. Напомним, что эта величина играет существенную роль в раскачке колебаний [•].
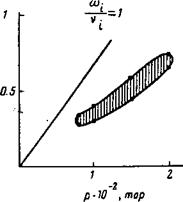
Если условие ш./. » 1 считать необходимым для раскачки колебаний, то получает объяснение ограниченность области неустойчивости со стороны малых давлений. Действительно, с уменьшением давления в области неустойчивости должно падать и магнитное поле. Неустойчивость прекращается, когда ларморовский радиус ионов сравнивается с радиусом трубки. Оценки нижнего предела по давлению, полученные таким способом, согласуются с данными эксперимента.
|
«>о |
![]()
|
Рис. 5. Экспериментальная граница существования падающей по частоте ветви низкочастотных колебаний в аргоновой плазме в соленоиде с 1г=60 см. |
 Диффузия электронов вдоль магнитного поля играет в рассматриваемых колебаниях двоякую роль. С одной ■стороны, она необходима для раскачки колебаний [•]. В то же время при достаточно малой продольной длине волны колебаний она может застабилизиро- вать неустойчивость. По-видимому, именно по этой причине неустойчивость не наблюдалась при наименьшей длине соленоида 20 см.
Диффузия электронов вдоль магнитного поля играет в рассматриваемых колебаниях двоякую роль. С одной ■стороны, она необходима для раскачки колебаний [•]. В то же время при достаточно малой продольной длине волны колебаний она может застабилизиро- вать неустойчивость. По-видимому, именно по этой причине неустойчивость не наблюдалась при наименьшей длине соленоида 20 см.
Неустойчивые колебания наблюдались лишь в «тяжелых» газах Аг, Кг,
Хе и отсутствовали в «легких» Не, N6.
Это обстоятельство мы расцениваем как
Прямое указание на важную роль эффектов конечного ларморовского радиуса в механизме неустойчивости.
4. Влияние эффектов конечного ларморовского радиуса ионов на дрейфовые колебания сдабоионизированной замагниченной плазмы
В большинстве работ, в которых исследовались колебания слабоиони - зированной плазмы, ионы считались холодными. Низкая температура ионов (Г,- Тв) характерна для ВЧ разряда и положительного столба. Однако, например, плазма разряда послесвечения является изотермической (2 « Г#). В этом случае, как отмечено в [•], эффекты конечного ларморовского радиуса оказывают существенное влияние на дрейфовые колебания в сильных магнитных полях 1. При >> 1 дрей
Фовые колебания могут раскачиваться под действием дрейфово-диссипа - тивного механизма [•• •]. При этом неустойчивыми оказываются «высокочастотные» колебания с со ^ V., поэтому ниже мы включили в рассмотрение инерцию ионов.
При и),./V, 1 электроны и ионы дрейфуют под действием стационарного радиального электрического поля примерно с равными скоростями II^ (.сЕо! Н) ^/«>51 сЕ01Н]. Такое движение приводит
Лишь к допплеровскому сдвигу частоты в лабораторной системе координат. Малое различие в скоростях дрейфа вызывает азимутальный ток, который, вообще говоря, мог бы повлиять на устойчивость плазмы [4]. Однако если электрическое поле является амбиполярным, то его воздействие оказывается слишком слабым и поэтому нами не учитывается.
Таким образом, из (П.1) и (2) было получено
(_*+о4фй+(^й_л^=во1 (13)
Здесь &5 = к2, -{- А£>|/(о£, ^10(2<) = е~г<Ь(2*)- Уравнения (13) и (14) дают частоту колебаний и границу неустойчивости (1шо)==0)
|
|
|
(16) |
![]()
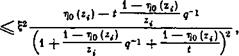 Подстановкой (15) в (16) получим
Подстановкой (15) в (16) получим
Где
![]()
|
Р ^ ІЯ*І (1 + * - По (»<)) + (1 — По (»<)) *]» |
![]()
|
Неравенство (17) можно переписать и виде |
![]()
|
(18) |
![]() Мо (*<) Я — (1 — По (**)) t
Мо (*<) Я — (1 — По (**)) t
Анализ этого неравенства показал, что при увеличении £ (т. е. при уменьшении давления нейтрального газа) первыми начинают раскачиваться колебания, вытянутые вдоль магнитного поля с Щ« к? (1+ -}-2^)(у<у#/а)<и)#). Критическое значение параметра £ оказывается равным £*=2 (^--TiITв)lI^. При 7^=0 этот результат совпадает с полученным в [3]. Таким образом, с увеличением ионной температуры для раскачки дрейфовых колебаний требуются бблыпие градиенты плотности плазмы ила меньшие давления нейтрального газа. Стабилизирующий эффект, по - видимому, обязан ионной диффузии.
Авторы благодарны Б. Б. Кадомцеву и Б. Н. Швилкину за полезные обсуждения.
ПРИЛОЖЕНИЕ
Вывод дисперсионного уравнения
|
Кинетическое уравнение для возмущения функции распределения ионов:
|
Было получено - линеаризацией (1). В выражении (П. 1) Д— возмущение - функции распределения; /0 — начальная функция распределения; <рх, — возмущение потенциала и плотности ионов. Начальное электрическое поле - считалось постоянным, Е0 — const, поэтому для решения (П. 1) удобна перейти в систему координат, в которой начальное электрическое полеравно нулю
|
|
°х И t/—скорость ионов в. новой системе координат, а ”-------------- rF. lH----
|
|
Скорость дрейфа в скрещенных полях. Тогда уравнение глядеть следующим образом:
|
|
Уравнение (П. 2) решалось интегрированием по траекториям, которые имели вид
V'x = VL sin (о).t - f - a),
1/=их cos K*+ot), x' = xQ — ~ cos (&Ј + a) +cos a>
У' — Ул + "~ sin W + *) —sin “•
В дальнейшем штрихи у vx, v x, у опускались.
Для возмущения функции распределения ионов имеем
TOC o "1-5" h z 5T=^V'f, i57—V‘A + Woo(v + “)- (П. 3)
Возмущение потенциала [<рх (г, £)] и возмущение концентрации [лА (г, £)] выбирались в виде е~ш+*к*У+*к*г. Интегрируя (П. 3), можно получить следующее выражение для Д(г, t):
U (Г, t) = l^n1fMe"SFr 2 о, + -
*=—ш
—7^/00 Wl + х(г + Z~)) — "о [(* +*(* + zj)) (® + г,<) —
Т. У“< Л уХ“1 ^ /, (S) ь, п0. /■ трыЛ
M/(vJ + w5) w<x^/J ^ ш +<v* — k, vM — nuii + )
П——со
E-»5sin«+»*»
2 у ■(5) _ (v‘ <•+iv-)) х
*=—со
TOC o "1-5" h z и 7 e-.5sin«+.*« 1
Е 1 (П. 4)
V.__________________________
JmJ W + iv,. — — По> ■
Я=—со
Здесь УІ == у* --v2r = fctfjub, (3, = m. uwJkTi, sin ф = &/VP5 — 1- Интегрируя (П. 4) по скорости, получим
*=—со /
|
( |
. тJCyX / 'ArrifU _
І+< vs 2 /. (I<) е-^ (р.)+
*=—00.
+ *#i;Tu>; + vJV + + “11 I
00
Х 2 n/.W (Р.) + *», (l - ^Г<1 + т^,.) X *=—00
Х. Ja> 2<<Г’< (/; {Z<) ~ 7* (Z<)) W (Р”))]} • (Н - 5)
В (П. 5) использовались следующие обозначения: W (ря) — интеграл вероятности от комплексного аргумента рл = (u> - f* Ь — ги£>{)/кжит; /„ (z{) — функ-
2093
Ция Бесселя мнимого аргумента; zi = AЈpf; vT = yjTJm^ При (D<vj(
| (u> - j - *vi — пи>4)1кяит | 1 (П. 5) можно переписать в виде
2j{.(l _st)-k, u(l + 53)^+ ь, (1 - %(*<) - ^)}=
=-{*< (1-1» (*,) •- 5i) + § ЈI(V+ Ц $. (П. 6>
Здесь
Я-1
S2 = 4 2 л2т)» (zi) 7^qr^|)2 *
*«•1
Уравнение (П. 6) записано в лабораторной системе координат (ш -*■ ш — ка)^ В случае замагниченных ионов a^/v, 1 при ш ^ из (П. 5) можно получить.
(-„.-V)+0«|L^a>)2+
+И^(< >)?=»•