ФИЗИКА ПЛАЗМЫ

«МАГНИТНЫЙ БЕРЕГ» В ОТКРЫТЫХ ЛОВУШКАХ ЗВОНКОВ А. В., ТИМОФЕЕВ А. В

Введение

В открытых магнитных ловушках естественным образом осуществля­Ете«! Конфигурация магнитного поля, называемая магнитным берегом (УВоЦВо). При ионном циклотронном нагреве плазмы, находящейся в та­ком магнитном поле, полностью поглощаются альфвеновские колебания, набегающие на область циклотронного резонанса со стороны большего магнитного поля [1]. Поэтому в открытых магнитных ловушках имеется возможность весьма эффективного ВЧ нагрева ионов. Однако для того что­бы выяснить, насколько реален такой нагрев, необходимо решить задачу

О Подведении ВЧ энергии к области циклотронного резонанса. Ее решение затрудняется двумерной неоднородностью системы: плотность плазмы ме­няется в направлении поперек магнитного поля, а величина поля —в про­дольном направлении. Часто в открытых магнитных ловушках характер­ный поперечный масштаб мал по сравнению с продольным. Основываясь на этом обстоятельстве, мы предположили, что при распространении вдоль магнитного поля колебания в любом сечении плазменного столба успевают принять вид собственных. При этом параметры колебаний меняются ади­абатически, т. е. так, чтобы номер радиальной моды оставался постоян­ным.

Найдено, что по мере приближения к зоне циклотронного резонанса альфвеновские колебания концентрируются к оси плазменного шнура. Это обстоятельство повышает эффективность циклотронного нагрева ионов. Показано, что альфвеновские колебания лучше всего связаны с возбуж­дающими антеннами в области, где выполняется условие й)Р»2/((о<2—<о2)~ ~(с/гою)2. Здесь й)р< — плазменная ионная частота, — ионная циклотрон­ная частота, г0 — характерный поперечный размер плазмы. Если возбуж­даемые колебания имеют достаточно широкий спектр продольных волно­вых чисел, то за счет явления трансформации в точке альфвеновского ре­зонанса значительная часть энергии будет передаваться коротковолновым электронным колебаниям. В последнем случае может наблюдаться интен­сивный нагрев электронов.

1. Основные уравнения

Рассмотрим колебания плазменного цилиндра, однородного в азиму­тальном и продольном (вдоль магнитного поля) направлениях. Для описа­ния колебаний используем систему уравнений Максвелла с известным тен­зором диэлектрической проницаемости холодной плазмы (см., например^ [1, 2]). Выразив г, 0-компоненты полей из соответствующих компонент уравнений Максвелла и подставив их в г-компоненты уравнений Максвел­ла, получаем

TOC o "1-5" h z 4л С 1

(£,+1)В,+£,(-гЛГ, Е,) =—г.. 2 гоЬьт, (1)

А)" УУ, — 1

£.В,+(£,+£,) (-гЛГ. ЕЛ =— (2)-

Й) /V г~— 1' /

+ т(1Ъ^~)Х £,“^((т) Дх+еа)’ в-1+«**/(«,*-«*),

^=й)Р<гй)/(й)1[75]—аг)й)„ 83=1—о)Р(?[76]/й)г, £>= (е—./V,2)2—#*, Л^,=А:гс/й),

Т — азимутальное волновое число. Здесь ЕГ, В* обозначают образы Фурье соответствующих величин, индексы т, /сх у них для # краткости опущены. В (1), (2) учтено, что в вакуумной области, за границей плазменного шнура, могут быть установлены антенны, в которых возбуждаются сто­ронние токи и заряды.

Анализ системы (1), (2) показывает, что в плазме возможны колеба­ния двух типов: с (альфвеновские и магнитозвуковые) и с Ег~Е±

(см., например, [2, 3]). Последние будем называть электронными, так как в них существенную роль играет инерция продольного движения электро­нов. При одинаковых значениях ю, т, Nг эти колебания различаются сво­ей радиальной структурой: радиальное волновое число электронных коле­баний значительно превышает радиальные волновые числа альфвеновских и магнитозвуковых. Если в плазме отсутствует так называемая точка альфвеновского резонанса, т. е. не выполняется равенство Г=Nt[77]1 то коле­бания с разными радиальными масштабами не связаны друг с другом. В этом случае система уравнений (1), (2) приближенно распадается на два не связанных между собой:

TOC o "1-5" h z Ал с 1

(£,+1 )ВШ - 2 тг2 - Тго1,]СТ, (3)

От Nl —1

О_Д7 2 /л/

Дх+е,---------- Ч Еш =------------- (/..с+сЛрс). (4)

Е [78] О)

Поправки к первому уравнению имеют относительный порядок т,/л^(й)/ ./(о»—со), ко второму тв/т,(с/г0й)Р1)2. В дальнейшем из всех компонент элек­тромагнитного поля будет использоваться только Вг, у которой для крат­кости опустим индекс «2».

Ляризации плохо взаимодействуют с иопами в области ионного циклотрон­ного резонанса, поэтому не будут рассматриваться в дальнейшем.

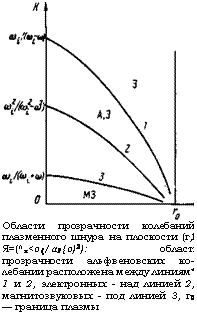Примем, что плотность плазмы меняется по параболическому закону л(г)=п0(1—(г/г0)2), а частота колебаний близка к циклотронной. При этих условиях радиальное волновое число альфвеновских колебаний дается вы­ражением

А«2'А:х((а1-(г/го)2)/(а2-1-(г/го)г)),/ (7)

Где Д1=1—#х2(|^(со,—й))/(1)р10, R^•.=Nzz((i)l2—

-й)2)/(|)р, о— 1, о)р,0=й)р,(0). При N:2>

2 2 >е (0) «(I)р<о/ ((I),2 — й)2) « й)р<0/2(|), ((|), — (!))

Из условия квантования получаем следую­щее дисперсионное соотношение для опре­деления собственных значений Л/,:

Кгг0(2(а1+аг))'К(х)-Е(х))^кр. (8)

Здесь К, Е — полные эллиптические инте - ■р гралы, У.=(ах!(а^аг)У /?> 1 — номер ра­диальной моды.

В той же области значений ради­альное волновое число электронных коле­баний равно

А:г»(й)р.0/с) (а2+(г/го)г

Соответственно дисперсионное соотноше­ние принимает вид

(й)р, оГо/2с) ((1-га2),/г+

+аг1п ((1+(1+а,),А)/а2'л))«яр. (9)

При №,*<е(0) в интервале (0. г0) имеется точка альфвеновского резонан­са г3(#*2=е(гв)). В ее окрестности #гА-*°о, N^-+0 (см. (5), (6)), и разде­ление колебаний на крупно - и мелкомасштабные становится несправедли­вым. Если исключить малую область значений Л^2~е(0), когда точка Г3 Близка к центру плазменного шнура, то система уравнений (1), (2) в ок­рестности этой точки сводится к одному стандартному уравнению четвер­того порядка с малым параметром перед старшей производной

Где L=(r-rs)a((щ2NJc(щi)z, A=|e3| (co»/iVxco)e(-c/aco)4, A=nr'ln7Lrs.

Уравнения типа (10) рассматривались неоднократно (см., например, [4—6] ). Из этого анализа следует, что крупномасштабные альфвеновские колебания, падающие на точку альфвеновского резонанса отражаются от нее в виде мелкомасштабных электронных. С другой стороны, мелко­масштабные колебания при. отражении от точки г3 полностью трансфор­мируются в крупномасштабные. Таким образом, при #х2<е(0) собствен­ные колебания представляют собой суперпозицию альфвеновских и элек­тронных, переходящих друг в друга в точке альфвеновского резонанса. Условие квантования для этого случая получено в Приложении (см. (П.8)). В силу соотношения &ГЭ>А:ГА в (II.8) можно не учитывать вклад альфвеновских колебаний. При этом дисперсионное соотношение прини­мает вид

(©рЛГо/2с)((1-|вг|)^-|в*|Ь((1 + (1-|в1|)%)/каГА))-яр. (11),

Здесь, как и выше, принято, что П(г)=п0(1— (г/г0)2).

3. Распространение колебаний вдоль магнитного поля

Рассмотрим сначала, что происходит с альфвеиовскимп колебаниями при приближении к точке циклотронного резонанса. Анализ соотноше­ния (8) показывает, что при этом х~а1-*-0, и само оно принимает впд

(<1)Р, оГо/2С) (со,/2(со,—Со)),/а (1 — М2со<(со.—Со)/со,?,<>) »Р•

Из последнего соотношения следует, что если со*-^со, то Nz2-+e(0)+g(0). При этом в соответствии с (7) (см. также рисунок) область прозрачности альфвеновских колебаний стягивается к центру плазменного шнура Дг/г0^ « 2 ((сосо) /со,)1/4 (С/ со р. оГо) ЧгрЪ.

В дисперсионные соотношения электронных колебаний (9), (11) маг­нитное поле входит лишь в сочетании Ntг/г(0)1 поэтому (#хэ)2= =Се(0) —► где С — константа порядка единицы.

При приближении альфвеновских колебаний к зоне циклотронного резонанса их область прозрачности сокращается, а радиальная компонен­та волнового вектора (в области непрозрачности 1т Кт) неограниченно возрастает. В результате связь альфвеновских колебаний с возбуждаю­щими антеннами, располагаемыми за границей плазмы, ослабляется. По­этому антенны лучше располагать вдали от зоны циклотронного резонан­са. Из предыдущих формул следует, что оптимальна область, в которой выполняется условие сОр10^(с/г0)((со<—со)/©)7*. В этом случае собственные альфвеновские колебания с небольшими номерами Р имеют одну и ту же (по порядку величины) амплитуду в области прозрачности и на границе плазмы. В плазме высокой плотности 710~ 1013—1014 см-3 при большом ра­диусе ловушки г0~100 см это условие не может быть удовлетворено в ме­дианной плоскости, и антенну, по-видимому, придется разместить в проб­ке, где плотность плазмы падает на несколько порядков.

В плазме более низкой плотности сор,0<(с/г0) ((со,—со)/©)7* собствен­ные альфвеновские колебания, как следует из (8), вообще отсутствуют. В этом случае собственные колебания с #х2>е(0) являются электронны­ми, а с УУх2<е (0) представляют суперпозицию электронных и альфвенов­ских. Если выполняется условие

Е(0) (г0со2/ссо,)г>1+2т(со/со<) +т2, (12)

То решение однородного уравнения (3) с УУх2=е(0) имеет бесконечно мно­го нулей в окрестности начала координат — происходит так называемое падение на центр[79]. Действительно, принимая при г-^0 /г(г)«/г0(1—(г/г0)2), из (3) получаем В~г где 7=—1±(1+2т(со/со,)+т2—е(0) (г0со2/ссо*)г)

Вырождение по радиальному волновому числу снимается и зависи­мость В (г) становится регулярной, если для описания колебаний исполь­зовать исходную — полную систему (1), (2). Таким образом, приходим к заключению, что при выполнении условия (12) имеется большое число собственных «электронно-альфвеновских» колебаний с близкими значе­ниями Nzг^г^0). С ростом плотности из этого «резервуара» выделяются собственные альфвеновские колебания с радиальным волновым числом Р—0, 1, 2, 3,... . Соответствующие значения параметра Ар=(Л^р со</сор<о)г возрастают при дальнейшем увеличении плотности (Ко>КС>Кг> ...).

Эти представления подтверждаются численным анализом однородного уравнения, соответствующего (3). Предполагалось, что плазма радиуса г0 с параболическим распределением плотности ограничена металлической стенкой, расположенной на радиусе г1Г (го=0,9/>). Была рассчитана за­висимость собственных значении параметра а2=#*2(со*2—©2)/©^о~1 от а=(соР1оГи7с)2. Собственные моды были найдены лишь при а>асг. Здесь

Асг=(1+2т(со/а)4)+т2) (ггг/г0)гю12(ю»2—со2)/со4

Соответствует «падению на центр». При А-+аст собственные значения А% Для всех мод стремятся к нулю, причем для Т=0 расчетные точки хорошо ложатся на прямые (7г) (а—аСт)ч*1паг=А(р+1)1 А«10. Для других ази­мутальных чисел получаются аналогичные соотношения с заменой правой части на А(р+Чг) для Тп=—1, А(р+31г) — Для Т=1, А(р+) — для Тп= =—2, А(р+2) — для Тп=2, Причем величина А во всех случаях практи­чески одинакова: А«9—10.

Можно показать, что такого типа дисперсионные соотношения и долж­ны получаться при а2-*-0. Действительно, при а2<1 в области А2'1г<^г1го<.1 Происходит падение на центр, и можно воспользоватся решением 2?«гт (см. выше), но ограничить минимальное значение г/г0 величиной Аг',г. Для набега фазы волны при этом получается выражение С (а—АсгУ^па^Х X(й)2/(о,(й)<г—(о2)71) (г0/гл*г) (С — константа), которое и определяет вид при­ближенных дисперсионных соотношений.

В заключение этого раздела заметим, что, как следует из (9), (И), рост плотности приводит к уменьшению значений собственных значе­ний К для электронных п электронно-альфвеновских колебаний.

4. Возбуждение колебании

А. Выше было показано, что при приближении к зоне циклотронного резонанса продольное волновое число колебаний неограниченно возраста­ет. При выполнении хотя бы одного из условий /с*2* (со,—(о)'/^«, Кг^ш/ит; Колебания интенсивно поглощаются частицами плазмы. Здесь уГ; — теп­ловая скорость частиц сорта /=е, I. Таким образом, колебания плазмен­ного шнура в продольно-неоднородном магнитном поле должны иметь вид волн, убегающих по направлению к точке циклотронного резонанса. Обычно при циклотронном нагреве в открытых ловушках имеются две точки циклотронного резонанса: одна — внутри ловушки, где удержива­ется сравнительно плотная плазма, другая — в запробочнон области, че­рез которую протекает разреженная плазма, выходящая из ловушки.

Существенно также, что размер антенны обычно мал по сравнению с характерным масштабом продольной неоднородности системы. Эти два обстоятельства (отсутствие волн, отраженных от зоны циклотронного ре­зонанса, и малый размер антенны) позволяют рассчитывать возбуждение колебаний в плазме открытой магнитной ловушки так же, как в случае однородного бесконечного плазменного цилиндра.

Альфвеновские колебания при циклотронном резонансе передают энер­гию ионам, в то время как электронные при определенных условиях могут поглотиться электронами. В открытых ловушках перегрев электронов мо­жет привести к вредным последствиям. Чтобы затруднить возбуждение электронных колебаний, необходимо электростатически экранировать ан­тенну и исключить протекание в ней продольных токов.

Возбуждение альфвеновских колебаний с #,2>е(0) может быть описа­но с помощью (3). Решение этого уравнения представим в виде

5(г)=Д (г, г') (4я/с) (Л^12—1)“1го1х]ст, (13)

Где £(г, г') — функция Грина уравнения (3)

1 (В^(г)В^(г) (г>г')

{Г, Г) иг{г’)в'-'(г)в^(г') (г<г')

В{±) (г) “ решения однородного уравнения, соответствующего (3), удов­летворяющие граничным условиям на правом (левом) конце рассматри­ваемого интервала: ¥(В{+)(г ), В{~}(г)) — функциональный определи­тель. У величин В (г), /(г), являющихся компонентами Фурье, как всюду в статье, для краткости опущен индекс Кх.

При значениях Кг, близких к собственным &*,р, функциональный опре­

Делитель IV можно представить в виде

СІІУ

У~

* -*Ж=^ г, р

Используя последнее соотношение, на*ходим прообраз Фурье (13)

/ Г1У _1 Л

Х№-1)-(—) Д,(г)га — (гВ,)|,_г.. (14)

1 * 2*"* Х, р

Здесь Вр(г) — собственная функция однородного уравнения (3), соответ­ствующая Кг=кгу, предполагается, что пространственная зависимость - сторонних токов, протекающих в антенне, имеет вид

/сТ(г)=б(г-Гв)С-в/(2)0°.

Аналитическое выражение для ВР(г) можно получить в квазиклассиче - ском приближении, когда

I Кг1' зт Кг С1Г ^ (г<гО

В,(г)*{ г, Ту

(*/,) | Кг|ехр( KrDrj (г>г,)

»“I

Г1

11 Г

Где Г1 — точка поворота (А:г(г4) =0), ^И7^А:Х= (—1)рА:г[80](га) —<1гкг. Вы -

Ак, о

Ражение (15) отличается от обычного квазиклассического представления решения волнового уравнения предэкспоненциальным множителем. Это отличие обусловлено слагаемым с первой производной в (3).

Подсчитаем энергию, расходуемую антенной на возбуждение альфве - новских колебаний. Плотность г-компоненты потока энергии дается вы­ражением

S^A=(c/8n)N2(NxAIDУ(gг+(г-NlгУ)B\ (16)

Напомним, что, начиная со второго раздела, под В понимается г-компо­нента магнитного поля. Используя (15), (16), находим поток энергии в од­ной моде альфвеновских колебаний

PЛ=(l/N')(Ulг/c)л^Ql. (17)

Р|

Здесь @1=(?(0)+|(0))/гг2е-2А| р^р/Мр)— величина, по порядку равная

О

С1

Единице при й)р1(,~с/го, Р=г/г0, ?=г/Ntг, g=g/Ntг, F, = — Ь(К(х)-Е(х) )*.

Ао

Р.

Б=л? Ий)((Ш1-й))/<орг„, А=к, г. 1<гР((Г-(1-г)!)/(1-г))

Р»

/т2=(^24-(1—ё)2) (^2—(1—е)2)-/*(1—?)“%, Множитель Е~гк Учитывает влия­ние области непрозрачности.

Б. Полученное выражение для Рк справедливо при Л£р>е(0). В обла­сти зпа'иш:ч А<е(0) альфвеновские колебания завязываются с элек­тронными, причем основная часть энергии переносится последними. По-

Ляризация электронных колебаний в области вакуума такова, что они не взаимодействуют с током /в, протекающим по антенне. Поэтому процесс возбуждения колебаний можно описывать с помощью уравнения (3). Разумеется, затем необходимо учесть трансформацию альфвеновских ко­лебании в электронные.

Продольная компонента вектора Пойнтинга электронных колебаний равна

TSxэ=(c/8л)^x(^xэ/D)2((e-ЛrI2)2(14-g2iVx2/eD)г+

+*2(1+(е-Л^)^7еЯ)2)|Я|2.

Здесь поле колебаний В может быть определено с помощью выражения (14), в которое в качестве ВР(г) следует подставить решение «электрон­ного» уравнения (4), связанное с решением (3) соотношением (П.5), описывающим явление трансформации колебаний в точке альфвеновского резонанса. Используя выражение для <1У1<1к1у полученное в Приложении (см. (П. 11)), находим полный поток энергии, переносимый одной модой электронно-альфвеновских колебаний (вклад альфвеновской части незна­чителен),

Р»-N.-**7* (0) (|Д,|7с)л’<?„ (18)

1

Где (?г=Ыа1,)г?(0)(п(гя)/п(0))Р,-ге-гл |рсгр^(р),

^ = - т^-Г((1-|аг|),'--|аг|1п((1+(1-|аг|),'')/|аг|''-)),

Ааг

Р *(р) — (п(0) 1п(р))Чя (ъ/ (1—£) ),/,Л-2( (1—ё)2Х Х(1+£7ёЯ)2+?(1+(1 -ё)2/ёЯ)2), Я~(1-г)2-г

Полная энергия, переносимая электронно-альфвеновскими колебания­ми, равна где РЭА^'кгэг0'^г0к1ез11^1~1 — число собственных мод

С /У22<е(0). Поскольку рассматриваются колебания с Агжг0—1 (см. выше) и Дг1> 1, то справедливо соотношение L*A/PA~Nг~i4:^. Таким образом, на возбуждение электронно-альфвеновских колебаний затрачивается лишь малая часть энергии, теряемой антенной.

В. В проведенном рассмотрении считалось, что при взаимодействии с антенной в плазме возбуждаются собственные колебания. Это предпо­ложение довольно естественно для быстрых альфвеновских колебаний Т^гА=с2(о/^А:г—с/7Ух. Однако оно может нарушаться для электронно-альфве­новских колебаний, поскольку радиальная компонента групповой скорости электронных колебаний довольно мала: У?~с^1(ьрш. Если за время про­хождения мимо антенны электронные колебания не успеют пробежать свою область прозрачности (г3г0), то и собственные колебания не успеют установиться. Это условие можно представить в виде

(Ып) ( У*/У*) ~Л(£/Го) (0)г/0)р.) <1,

Где Ь — размер антенны по С^, Уяэ~сШг.

Кратковременное взаимодейетвие электронно-альфвеновских колеба­ний с антенной можно рассчитывать, полагая, что в области прозрачности альфвеновских колебаний с Л^2<е(0) они убегают от антенны по направ­лению к центру плазменного шнура. Спектр таких колебаний, очевидно, непрерывен, и их можно описывать уравнением (3). Учитывая условие «излучения», для функции Грина в области прозрачности альфвеновских колебаний будем использовать выражение

TOC o "1-5" h z г Г'

С(г, г ) = (‘/2)(|ЛгА(г') |^гл(г))у, ехр(^ КгА<1г- |Кгл|Л"). (19)

П Г,

Здесь учтено, что в рассматриваемом случае источник (антенна) распо­лагается в области непрозрачности (г<гі<г &га(гі)=0).

С помощью (19) находим 2-компоненту магнитного поля альфвенов - ских колебаний

Г ГЯ

В=(2я/с);(ІУ//ІУ,)''’ехр(і| |А/|А-),

А затем, используя выражение для г-компоненты вектора Пойнтинга

5гА-(с/8я)(Л/)-‘|Вр,

Полную энергию, отдаваемую антенной

Р°*~{л[81]/Ъ)е-“(Г1/с) IЛк.Г„г\

Последнее выражение показывает, что если спектр колебаний тока в антенне достаточно широк Акг^г1~і'^г0~іУ то энергия, затрачиваемая на возбуждение электронно-альфвеновских колебаний, сопоставима с Р* (см. (17)). Поскольку в электронных колебаниях Е± и Ег сравнимы, они могут поглотиться как электронами, так и ионами. Как следует из (11) (см. так­же обсуждение в разд. 3), К^ при приближении к циклотронному резо­нансу меняется по закону Л:ЯЭА^— (оэ/с) (й)*і/(й)<—<о) )’ Учитывая, эту оцен­ку, находим, что при выполнении условия (©</юрі)*Л>ті,/,і>т."1<1 элек - тронно-альфвеновские колебания поглотятся электронами до того, как вступят в циклотронное резонансное взаимодействие с ионами.

За обсуждение работы авторы благодарны В. Л. Вдовину и И. А. Ко­вану.

ПРИЛОЖЕНИЕ

В гидродинамике Л Теория плазмы детально изучено уравнение

1 <24<р <2*<р

+ *—-г + Ф-о, (П.1)

Л

(см., например, [4—6]). Решения уравнения (10) выражаются через решения урав­нения (П.1) — С помощью этого соотношения находим асимптотики четы­

Рех линейно-независимых решений (10) в области прозрачности справа от точки трансформации

Виг ~ пН-'1' ехр(±2^,',±гя/4), (П.2)

В*« *ехр(±(21/3)ЛЧ''-±3«л/4). (П.3)

Здесь выражение (П.2) соответствует альфвеновским колебаниям, (П. З) - элект­ронным.

Из результатов, полученных в [4-6], следует, что электронные колебания, па­дающие на точку трансформации (§=0), отражаются от нее в виде алъфвеновских и наоборот. Соответствующие решения (10) имеют вид [5]

В^^В^-В?, (П.4)

Я<2)=я2а_я2э (П.5)

Отметим, что электронные колебания обладают аномальной дисперсией - радиаль­ные компоненты групповой и фазовой скоростей имеют противоположные знаки. Поэтому следует считать, что волна, бегущая направо, описывается 2?гэ, нале­во - В

Вдали от точки альфвеновского резонанса - в области, где система (1), (2) раз­деляется на независимые уравнения (3), (4), решения (П.2), (П. З) принимают вид

Г

Виг * я* (кгЩ) * ехр ( ± I | ± &«/4 ) ,

Г»

Г

Виг * л*Л-''‘фДгэ)',! ехр ( ± < <1т±ЫпИ ) ,

Г»

Где р—6/йг=а{(агУг/ащ)гч ЛГА, Кгэ определяются (5), (6)

Области прозрачности альфвеновских и электронных колебаний ограничены справа обычными точками поворота квазиклассических колебаний П и Гг*г0 соот-

»су с а Л* ТОЧКИ воспользуемся СООТНОШв - Риями

TOC o "1-5" h z Г. Г

(я*,А/р)'Л8т( j KSdr+M) ~(7г)(л1*гА|/Р)71ехр( - J |*,А|*-) , (П.6)

Г Г|

-Я*Л-* (Р/*,3) * sin ( J *гэ <гг + — ) — - (■/») л7,Л_1‘ [р/1 Яг,31) exp ( - j | *,э | dr ) .

Г Г,

(П.7)

Здесь коэффициенты подобраны из соображений удобства дальнейших вычислений. Эти выражения сопрягаются в точке альфвеновского резонанса Г8 с помощью со­отношении (П.4), (П.5). При этом получаем условие квантования

И Г,

J*,3dr - J*,Adr-JiO> + 7t). (П.8)

Гв га

Приведем еще несколько полезных соотношенпй. Для расчета функционального определителя, входящего в (13), (14), необходимо знать решения однородного урав­нения (3), удовлетворяющие граничным условиям на правой —£(+) и левой — £<-> границах. Условию на правой границе удовлетворяет выражение (П.6). Слева интер­вал распространения альфвеновских колебании ограничен точкой трансформации. Чтобы получить £?<->, следует преобразовать решение (П.7) уравнения электрон­ных колебаний (4) в решение уравнения (3) с помощью соотношений (П.4), (П.5). При этом получаем

TOC o "1-5" h z Г U

В(->- (пкгЩ% sin ( J *,* Dr+Nli - j*,» Dr ) . (П.9>

ГШ Ra

Функциональный определитель для решений (П.6), (П.9) равен

»*1 »*•

1Р-(В<+>)'В<->-(В(->)'ВС+>-(я/р)(*,.л)г sin ( J KrA Dr - J К? Dr j. (П.10)

*• ГШ

При собственных значениях iV, с помощью (П.8), (П.10) получаем

-«=(-1)р(я/Р)(*га)’ —( Г K*Dr- f*,Adr) . (П.11)

X Dks * * /

Ra