ЭЦР НАГРЕВ ПЛАЗМЫ ДВУМЯ МОЩНЫМИ ЭЛЕКТРОМАГНИТНЫМИ ВОЛНАМИ
ЗВОНКОВ А. В., ТИМОФЕЕВ А. В.
1. Движение электрона в магнитной ловушке в присутствии мощного ВЧ монохроматического поля характеризуется релятивистским адиабатическим инвариантом, заменяющим магнитный момент [1] (см. также [2]). Этот инвариант сохраняется, даже если электрон попадает в зону циклотронного резонанса. Естественно, что существование адиабатического инварианта препятствует нагреву электронов в ВЧ поле. Эту точку зрения подтверждают, например, результаты экспериментов [3, 4], в которых наблюдалось упругое (без изменения энергии) отражение электронов от зоны циклотронного резонанса в адиабатической ловушке. Следует отметить, что возможность обратимого движения электронов в присутствии резонансного ВЧ поля была указана еще в [5].
Однако даже в том случае, когда движение электрона в мощном ВЧ поле является регулярным, оно оказывается довольно сложным. Это создает предпосылки для его хаотизации при усложнении спектра ВЧ поля. В настоящей работе показано, что расщепление спектра на две частота может хаотизировать продольное движение низкоэнергичных электронов с В±1тс2<(Е1В0)г, где ех — энергия движения электрона поперек магнитного поля, Е — амплитуда ВЧ поля, В0 — стационарное магнитное поле. Такие электроны возникают в магнитных ловушках, например, при ионизации нейтрального газа. Хаотизация продольного движения вызывает диффузию по е,|, однако при реальных значениях ВЧ поля максимально достижимые значения е(| оказываются сравнительно небольшими.
При движэнии вдоль магнитной ловушки высокоэнергичных электронов (г±/тсг^ (Е/Во)*) изображающая точка на фазовой плоскости пересекает сепаратрису — мгновенную фазовую траекторию, проходящую через гиперболическую особую точку. Пересечения сепаратрисы сопровождаются скачками адиабатического инварианта. В немонохроматическом ВЧ поле скачки становятся нерегулярными, в результате возникает диффузия по ех [1]. В настоящей работе получено выражение для коэффициента диффузии.
Отметим, что повышение эффективности нагрева при расщеплении спектра ВЧ поля наблюдалось в [6]. В [7] это явление объяснялось нарушением суперадиабатического режима движения электронов. Супер - адиабатическим принято называть регулярное движение электронов в ловушках в присутствии достаточно слабого ВЧ поля.
2. Движение электронов в присутствии ВЧ электромагнитного поля будем описывать слаборелятивистским гамильтонианом
|
|
(1)
Здесь і=*р±гсгІ(2еВ0(і)) — величина, являющаяся адиабатическим инвариантом в отсутствие ВЧ поля; А — амплитуда вектор-потенциала ВЧ поля; Ф=*0—О*, 0 —фаза циклотронного вращения электрона; Г — координата, отсчитываемая вдоль стационарного магнитного поля.
Как ив (1), рассматривается простейший случай колебаний с й)~о)„ правой поляризацией вектора электрического поля и длиной волны в направлении поперек магнитного поля, значительно превышающей электронный ларморовский радиус; эффект Доплера не учитывается. В [ 1 ] канонически сопряженными величинами являются |х, Фи Рь г.
Электрон, удерживаемый в магнитной ловушке, осциллирует вдоль магнитного поля, при этом его поперечная энергия колеблется под воздействием ВЧ поля. Будем предполагать, что частота «поперечных» колебаний намного превышает частоту осцилляций вдоль ловушки (баунс-час - тоту). Поэтому при рассмотрении поперечного движения, характеризуемого величинами ц, Ф, другую пару канонически сопряженных величин Рн, 2 будем считать медленно меняющимися параметрами. При таком движении сохраняется поперечный адиабатический инвариант, который в окрестности резонансной точки может существенно отличаться от ц. Условие адиабатичности имеет вид [ 1 ]
![]() (2)
(2)
Где Е=(О)/с) А — амплитуда ВЧ электрического поля, Ь — характерный масштаб изменения стационарного магнитного поля.
3. Вид фазовых траекторий на плоскости ц, Ф при фиксированных значениях рн, 2 довольно сложен [1]. Исключение составляют лишь траектории в окрестности эллиптической точки (ц,, 0), на которых величина ц меняется весьма слабо |ц(0_1,<(Е1В0)ч, тсг1(о. По таким орбитам движутся электроны, поперечная энергия которых вдали от резонансной зоны достаточно низка, Гх<тс2(Е1В0)ч Для в [1] были получены следующие выражения:
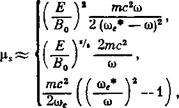
![]()
|
О) |
![]() (3)
(3)
Где А —(Е1Во)ч а)/=а),(1—Чг(р\!тпс)г). Предполагается, что точка циклотронного резонанса отстоит от минимума магнитного поля на
Из (3) следует, что при малой амплитуде ВЧ поля в области ю/<ю будет мала и поперечная энергия электрона. Однако если электрон, двигаясь вдоль магнитного поля, заходит в область то его поперечная
Энергия может достигать релятивистских значений, которые не зависят от величины электрического поля (см. нижнее выражение (3)). Легко видеть, что при в области ю/(2)>ю выполняется условие циклотрон
Ного резонанса <о=со*(е, Г). Состояние циклотронного резонанса поддерживается при движении вдоль неоднородного магнитного поля для электронов, захваченных в режим авторезонанса [1, 8].
В присутствии монохроматического ВЧ поля электроны совершают периодические осцилляции между пробками ловушки. При достаточно малой амплитуде ВЧ поля продольное движение электронов с ц»ц.(рц, 2) можно описать гамильтонианом
|
<*>><!)/ |
|
(4) |
|
|
|
|
Теперь предположим, что наряду с основным ВЧ электрическим полем в плазме возбуждено электрическое поле другой частоты (&<ю)
Меньшей амплитуды ЕХ<*Е. Воздействие этого поля на движение электронов будет особенно сильным, если разность частот ВЧ полей & кратна частоте колебаний электрона вдоль ловушки где Ыь~Р\1Тг1Ь. В том
Случае, когда соседние резонансы «перекрываются», продольное движение становится хаотическим (см., например, [9]). Известное условие перекрытия резонансов tfls>(l/le) (Dtob/DJ) (6/)2 в данном случае можно представить в виде
4 V Dp, / DPi' Q”
Здесь Hx, — резонансная составляющая возмущения Я, = (2шги/тс2) HEA tX Xcos(<D+Qf); / — действие, характеризующее продольиое движение электрона; Ы — расстояние между соседними перекрывающимися резонансами, производная Dwjdj представлена в виде (DbidwJdp^KdHJdpu), где Нь Рн ~ значения этих величин в области a)>a)/(z).
Анализ условия перекрытия резонансов для определенности произведем, счи'Ш! ловушку адиабатической. В таких системах зависимость a),(z) имеет минимум и симметрична относительно точки минимума, соответственно имеются две точки циклотронного резонанса Z=±Z,<. В этом случае Ни обращается в нуль при П=2к и перекрываются нечетные резонансы л=2/Н-1, что учтено в (5). Вычисление Я1я облегчается тем обстоятельством, что для рассматриваемых «авторезонансных» электронов с ВЧ поле «включается» в момент прохождения через резонансную точку и влияет на движение только в области <ав9(г)><й. Слаборелятивистские электроны заходят за резонансную точку на небольшое расстояние ^P^L/Mc. В этой рбласти имеем
/’Cos(®+Qt)- (6)
Здесь и ниже L=(B0'IB0)'Lts .
Из (4) нетрудно найти, что за резонансной точкой электрон движется по закону Z(T)^Za~-(P]]L/Mc)Sin(CtlL). Подставляя это выражение в (6), получаем
Пн '■тс ' с с
/ ..J 2р„ '4<льь я (л LQ л QL /
(а-) ЕЛ, ип2 Г“4")'
Условие перекрытия резонансов зависит от соотношения между разностью частот Q и обратным временем пребывания электрона в области за резонансной точкой —c/Z/l
|
(7) |
![]() OW(“r - “«*
OW(“r - “«*
Из (7) следует, что с помощью ВЧ электромагнитных полей, используемых в настоящее время (Е/Вв<10"4), электроны с Г±1тс2<(Е1В0)* могут быть нагреты до не слишком высоких энергий ^10*—103 эВ. Максимальная достижимая энергия возрастает с увеличением разности частот ВЧ полей, используемых для нагрева, и длины системы.
Коэффициент диффузии по продольному импульсу равен
|
П & UVv, ( |
![]() 2яаГ4(3/*) QW^/EiV QL (Я-1)* С Во' ' с
2яаГ4(3/*) QW^/EiV QL (Я-1)* С Во' ' с
|
|
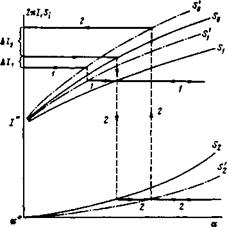
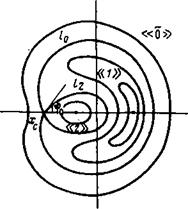 Рис. 1 Рис. 2
Рис. 1 Рис. 2
Рис. 1. Фазовая плоскость системы (1) в полярных координатах У2ц, Ф: Хс — седло -
Вая точка, 10, /2 - сепаратрисы
Рис. 2. Изменение адиабатического инварианта со временем. Жирными горизонтальными линиями и пунктирными вертикальными показана траектория электрона, цифры «1», «2» отмечают два варианта траектории после пересечения сепаратрисы
^о, 5/- значения площадей при двух значениях параметра А*=^31г^ъ
В настоящем рассмотрении движение электронов считалось адпабатич - ным, что справедливо, если частота осцилляций ц при значитель
Но превышает разность частот ВЧ полей £2. Это условие накладывает ограничение на максимальное значение & (£2<о) (р^/тс) (ЕХ1В0)Ъ).
4. Рассмотрим теперь движение электронов с большой поперечной энергией Е±/тс'^(Е/В0)11г. Как и в предыдущем разделе, будем считать, что характерная частота изменения ц, Ф намного превышает частоту осцилляций вдоль ловушки о)й и частоту биений й. В этом случае сохраняется поперечный адиабатический инвариант /=£/2л, где 5 — площадь, охватываемая траекторией на фазовой плоскости ц, Ф. Фазовый портрет системы при о)/—а)> (3/2) со(£Г/-в0),/в изображен на рис. 1. Размер областей «1», «2» меняется при изменении параметров о)е(2(^)), А(Ь). Более того, с уменьшением (о/ область «2» стягивается в точку (при а)/=а)(1+ +3/г(Е/В0)Чг) и затем исчезает. Одновременно сепаратриса 10 превращается в регулярную траекторию. Площадь области Я1 в момент исчезновения равна 2л/*=3/2этр* где р=8(е^4/со)(тс2/со),/а (см. Приложение).
Если при некотором значении медленно меняющегося параметра площадь области, в которой находится изображающая точка, окажется равной 2л/, то фазовая траектория выходит на границу области (сепаратрису) и дальнейшее измененне параметра приводит к переходу траектории в другую область. (Для траекторий, находящихся в области «0». критическим значением является 1=(§1~-32)/2л). При этом адиабатический инвариант может измениться на б/—/.
При Е{/Ес{ основные изменения областей 5, обусловлены вариациями о)е(г) при движении электрона вдоль ловушки. В [1] отмечено, что в случае Е!=0 изменения адиабатического инварианта из-за пересечений сепаратрисы при таком движении с хорошей точностью обратимы. Соответственно при ^!=0 диффузия по ех оказывается весьма слабой. В то же время присутствие даже небольшого ВЧ поля другой частоты может существенно усилить диффузию [1]. В настоящем разделе будет найден коэффициент. диффузии под действием двух ВЧ монохроматических полей с различающимися частотами.
Процесс изменения адиабатического инварианта иллюстрируется рис. 2, на котором изображены зависимость площадей 52 и 50, охватываемых сепаратрисами 1г и 10, а также их разности 51=5о—52 от параметра а=
=4тс*(а),(2)— (1))/(1)2. Если траектория на фазовой плоскости не пересекает сепаратрису, то адиабатический инвариант сохраняется. Этим участкам траектория на рис. 2 соответствуют горизонтальные отрезки (ордината равна значению адиабатического инварианта).
Пусть электрон движется в сторону увеличения й)е(г) и сначала его траектория охватывает сепаратрису 10: />/*. В некоторой точке 50 сравнивается с 2л/ — частица пересекает сепаратрису. При этом она может захватиться в области «1» или «2» с вероятностями р1=^1/^0 и Рг^Зг/Зо Соответственно (см., например, [10]). Далее электрон продолжает движение с новым инвариантом. К моменту обратного перехода через сепаратрису кривые из-за зависимости А от времени смещаются (на рис. 2 новые положения изображены штрихпунктирными линиями), вследствие чего обратный путь не совпадает с прямым. В нашем случае смещение кривых невелика, так как мы полагаем, что одна из волн имеет малую амплитуду и, следовательно, А(*)=Л(1+6соеЭД, 6*=АХ! А. При этом нетрудно найти результирующее изменение адиабатического инварианта Д/ для каждого из путей
2л' Да д$ ар Да 'V Да ' н ’
Где I, /—1, 2, **■/, 2рбзт(&Д^/2)зт(1|>о+&Д*</2), Д*< — время между
Пересечениями сепаратрисы; номер траектории на рис. 2 совпадает с номером области, в которую попадает электрон из области «0».
Полагая фазу модуляции в момент пересечения сепаратрисы случайной величиной, можно написать коэффициент диффузии по /:
— «(ДЛГ>*Р.+<(ДЛ)%Л). (9)
Л
Будем считать, что в силу малости 6 справедливо неравенство | (д5</да)а|>|(д5</д[))[&|, тогда для вероятностей Pi имеем
ДБ{ / ДБ0
Да ' да
Кроме того, для простоты рассмотрим Случай АА1>1, при этом коэффициент диффузии максимален. Полагая зт2(ЙД*/2) =!/а и используя фор
Мулы, полученные в Приложении, можно привести выражение для £)/ к компактному виду
1 /«.*/ ДБ* X-1
В случае траекторий, близких к предельной сепаратрисе, т. е. при /—/*<^ </*, получаем
TOC o "1-5" h z 4 / 1—1 1/4
• (11)
В обратном предельном случае (/>/*) имеем
8 ■ 2'л / / ‘/‘
• (12)
Выражение для Г можно представить в виде /*= (Злгс2/ю) (£/2?0)*
Величина ц на траектории электрона не остается постоянной, однако в области, где ©/<©, вдали от резонансной зоны ц«//2л=сопз1. Это соотношение позволяет связать с коэффициентом диффузии по ц (£)„=/)//4л2). В процессе диффузии импульс электронов может возрасти
До значений, по порядку величины не превышающих Тс8'/'(Ех/В0Уг''Х Х^Ыс)*'*. Данное ограничение следует из условия стохастизации движения (<2т|)/^/)Д/^1, где ф=я£2/й)б ~ Набег фазы в гамильтониане Нх За одно прохождение электрона по ловушке, величина Д/ определяется (8). Для электронов, рассматривавшихся в настоящем разделе (рх1тс^(Ех1Во)1*), Условие адиабатичности имеет вид (р±/тсЕ/В0)'1* (ср. с разд. 3).
Таким образом, в настоящей работе продолжено исследование ЭЦР нагрева плазмы в мощных ВЧ полях, начатое в [1]. В [1] было обнаружено падение эффективности нагрева при превышении электрическим полем критического значения, определяемого условием (2). Из рассмотрения, проведенного в данной работе, следует, что в этом случае ВЧ энергию выгодно распределять между несколькими частотами. В немонохроматическом ВЧ поле особенно интенсивно должны нагреваться электроны, начальная энергия которых не слишком мала, е^тс2(£72?0)%.
За обсуждение работы авторы благодарны В. Л. Вдовину и А. И. Ней - штадту.
ПРИЛОЖЕНИЕ
Для определения величин 5<, ДБіІдА, ДБіІд^ воспользуемся результатами работы
[10] , где анализировалась система, описываемая гамильтонианом вида
//=C4i-|A2+ЯV|A COS Ф.
При а=4тс2({|>#(*)-<1))/<1)2, Р~8(єі4/ш) (тсг/<а)Чі он совпадает с гамильтонианом поперечного движения электрона Н-рйг/2т (см. (1)).
В [10] были получены выражения для площадей 5<: 5о*=сс(я-фо) +3|хс| (а - - хс2)7* зіпфо, 5^2^0-сш, £2=ая-£0, где Хе - декартова координата седловой точки на рис. 1; фо=агссоз((а-2хс2),/,/2|хс|) - угол, под которым сепаратриса пересекает Ох. Значение хе определяется уравнением
4*с3—2oxc-Я=0.
![]() Приведенные выше выражения для & позволяют вычислить все производные д5,/да, ДSdд$. Однако более простым оказывается использование общей формулы, полученной в [10],
Приведенные выше выражения для & позволяют вычислить все производные д5,/да, ДSdд$. Однако более простым оказывается использование общей формулы, полученной в [10],
(П.1)
Где ^ - произвольный параметр, от которого может зависеть гамильтониан; Нс - Значение гамильтониана на сепаратрисе.
В [10] с помощью (П.1) были определены величины д£о/да»л-Фо, д^/да« «=я-2ф0, №/да*»фо. Аналогичным образом нетрудно найти Д8о1д$=д8х12д$= =-д£2/0р=зш фо (а-2хс2)