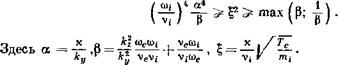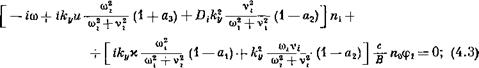ДРЕЙФОВО-ДИССИПАТИВНАЯ НЕУСТОЙЧИВОСТЬ НЕОДНОРОДНОЙ ПЛАЗМЫ В МАГНИТНОМ ПОЛЕ
А. В. Тимофеев, В. Н. Швилкип
ВВЕДЕНИЕ
В настоящее время неустойчивость плазмы в магнитном поле стала привычным явлением. Один из первых экспериментов, заставивших говорить о неустойчивости плазмы, был описан Бомом и др. *. В этом эксперименте был обнаружен аномально быстрый уход плазмы сквозь магнитное поле на стенки сосуда. Для объяснения этого явления в 1 предположили, что в плазме самопроизвольно возбуждаются хаотические электрические поля. В таких полях заряженные частицы движутся беспорядочно, что приводит к усиленной диффузии плазмы через магнитное поле. Для коэффициента диффузии Бом дает эмпирическое выражение D — (1/16) cTJeB— бомовский коэффициент диффузии, где Те — электронная температура В[- магнитное поле. Позднее аномальная диффузия плазмы с коэффициентом диффузии порядка бомовского была обнаружена в системах, существенно отличных от описанной в 1. В настоящее время бомонскую диффузию принято связывать с самопроизвольным возбуждением так называемых дрейфовых колебаний, см., например, 2.
В данном обзоре рассматривается один из возможных механизмов раскачки дрейфовых колебаний, в котором существенную дестабилизирующую (!) роль играют столкновения заряженных частиц 3. В 4 на основе анализа
© Главная редакция физико-математичесной литературы издательства «Наука», «Успехи физических наук», 1976
6 УФН, т. 118, вып. 2
Размерности величин, характеризующих неустойчивые колебания, была сделана попытка получить бомовский коэффициент диффузии [43]).
Причиной интересующей нас неустойчивости является термодинамическая неравновесность плазмы — градиент давления в направлении поперек магнитного поля. Такая неравновесность неизбежна во всех системах, использующих магнитное удержание плазмы, поэтому неустойчивость была в работе 5 названа универсальной. Заметим, однако, что на самом деле для развития неустойчивости градиент давления должен превысить некоторую критическую величину, определяемую размером плазмы вдоль магнитного поля, концентрацией нейтральных частиц и т. д. Поэтому неустойчивость будет развиваться далеко не во всех установках. В работе 6 для обсуждаемой неустойчивости был использован термин — инерционно-диссипативная неустойчивость. Это название отражает ту ее особенность, что, хотя электроны при развитии неустойчивости из-за частых соударений с тяжелыми частицами (ионами в полностью ионизованной плазме, нейтральными атомами в плазме слабо ионизованной[44])) движутся как в вязкой среде, движение ионов должно быть свободным — инерционным. В настоящее время наиболее употребительным является третье название: дрейфоводиссипативная неустойчивость, которое было предложено в работе 8. Это название подчеркивает важную роль дрейфовых движений в механизме раскачки колебаний. Первоначально термин дрейфово-диссипативная неустойчивость употреблялся в обобщенном смысле, так что в диссипативные процессы включалось и бесстолкновительное затухание Ландау. Соответственно к дрейфово-диссипативным неустойчивостям относили и неустойчивости неоднородной разреженной плазмы в магнитном поле (см., например,8'9). Однако со временем термин дрейфово-диссипативная неустойчивость стал употребляться лишь для обозначения неустойчивостей столкновительной плазмы. В этом более узком смысле мы и будем использовать название дрейфово-диссипативная неустойчивость.
Основные положения теории дрейфово-диссипативной неустойчивости были установлены уже в первых работах, посвященных ее анализу. Последующие исследования добавили к этим результатам мало нового. Столь быстрое развитие теории во многом обязано использованию так называемого локального квазиклассического приближения. В этом приближении неоднородность плазмы учитывается параметрически, что позволяет получить локальное алгебраическое уравнение, определяющее частоту плазменных колебаний. Первоначально высказывались сомнения относительно правильности этого метода (см., например, 10). Однако дальнейшие исследования (см., например, 9'и) показали его адекватность для широкого класса колебаний неоднородной плазмы в магнитном поле, в которых существенную роль играют дрейфовые движения заряженных частиц. К этому классу относится и дрейфово-диссипативная неустойчивость.
Дрейфово-диссипативная неустойчивость — довольно «слабая» неустойчивость. Если одновременно в плазме развиваются какие-то другие неустойчивости, то дрейфово-диссипативную трудно выделить на их фоне.
Поэтому экспериментальное исследование дрейфово-диссипативной неустойчивости желательно проводить в условиях, максимально приближенных к равновесным. Часто неравновесность плазмы обусловливается самим способом ее создания (пропускание сильного тока через газ, инжек - дия пучков заряженных частиц и т. д.). В этом смысле наиболее «спокойными» являются системы двух типов: бестоковые газовые разряды и (7-машины. Термин бестоковый газовый разряд иногда используется (см., например,12) для обозначения таких типов разряда, поддержание которых не связано с пропусканием постоянного тока через газ. К ним относятся высокочастотный разряд, разряд послесвечения, пеннинговский разряд и т. д. Газовый разряд постоянного тока в магнитном поле подвержен более «сильной», так называемой токово-конвективной неустойчивости. Обнаружение этой неустойчивости 13,14 и ее успешная идентификация в15, наряду с в значительной мере стимулировали исследования колебаний всех видов газового разряда в магнитном поле. Следует отметить, что хотя в разряде постоянного тока в магнитном поле может развиваться токовоконвективная неустойчивость, однако это обстоятельство не ставит непреодолимых препятствий для наблюдения дрейфово-диссипативной неустойчивости, см. ниже.
^-машины с самого начала были задуманы как системы, предназначенные для изучения спокойной (quiescent) плазмы. В них плазма создается термической ионизацией пучка нейтральных атомов, падающего на накаленную пластину.
В исследовании колебаний плазмы (>-машип и бестоковых газовых разрядов в магнитном поле можно выделить два этапа. На первом преобладала тенденция относить все неустойчивости, обнаруженные в столк - новительных режимах, на счет проявления дрейфово-диссипативного механизма раскачки колебаний. Более внимательное изучение вопроса, однако, показало, что одновременно с дрейфово-диссипативным могут действовать и другие механизмы. Постепенно крепло убеждение, что лишь прямая проверка дисперсионного соотношения позволит решить вопрос
О природе наблюдаемых колебаний (дисперсионное уравнение определяет зависимость частоты колебаний от компонент волнового вектора колебаний и параметров плазмы). Такая проверка к настоящему моменту осуществлена для большинства разновидностей дрейфово-диссипативной неустойчивости. Ее положительные результаты позволяют говорить о дрейфово-диссипативной неустойчивости, как о твердо установленном физическом явлении.
1. ОБЩАЯ ХАРАКТЕРИСТИКА ДРЕЙФОВО-ДИССИПАТИВНОЙ
НЕУСТОЙЧИВОСТИ
А) Исходные уравнения
Процессы, приводящие к развитию дрейфово-диссипативной неустойчивости, могут быть проанализированы в приближении двухжидкостной гидродинамики. При использовании этого приближения электронная и ионная компоненты плазмы представляются в виде двух взаимно проникающих жидкостей или, точнее говоря, газов. Для изотермических процессов, которые будут рассматриваться ниже, система гидродинамических уравнений сводится к уравнениям неразрывности и уравнениям движения каждой из компонент плазмы. Уравнения неразрывности имеют стандартный вид
-|- + УМ = 0, (i. i)
Где индекс ) принимает два значения: / = е, £ для электронов и ионов соответственно. Плазма считается квазинейтральной пе = = п.
Уравнения движения следует обсудить более подробно. Нас будут интересонать сравнительно медленные процессы, частота которых ш мала по сравнению с ve-чacтoтoй соударений электронов с тяжелыми частицами (нейтральными атомами в слабо ионизованной плазме, ионами в плазме полностью ионизованной). При рассмотрении таких процессов в уравнении движения электронов можно опустить силу инерции
0= — теуп — еп ( — + (!-2)
"здесь магнитное поле считается постоянным и однородным, а электрическое поле потенциальным Е = — Уф, что справедливо для плазмы низкого давления 8лпТ/В2^ 1. В дальнейшем мы будем рассматривать колебания плазмы с замагниченными электронами, когда электронная циклотронная частота ше значительно превышает мр. Оказывается, что в этом случае трение влияет лишь на движение электронов вдоль магнитного поля. Поэтому мы положим = 0, ^||е = — тпе№цее, здесь и в дальнейшем значки «продольно» и «поперечно» отмечают направление относительно магнитного поля. Вообще говоря, вместо Уце в выражении для силы трения должна стоять разность ице — Уцп в случае плазмы слабо ионизованной или Уце — уц; в случае плазмы, ионизованной полностью. Однако в плазме, называемой слабо ионизованной, заряженные частицы составляют малую долю 10~4 от общего их числа. Поэтому заряженные частицы не могут вовлечь в движение нейтральную компоненту плазмы, и последнюю можно считать неподвижной, положив Уцп = 0. Поскольку продольная электронная скорость Уце значительно превышает ионную 1?ц;, то же самое выражение для силы трения остается приближенно справедливым и в случае полностью ионизованной плазмы.
Ионное уравнение движения запишем в виде
Т>п^=- — Т&п + еп ( — Уф + ^-[угВ]) + Р,; (1.3)
Здесь в случае слабо ионизованной плазмы Г; = — где vг —
Частота ион-нейтральных соударений. В плазме полностью ионизованной трение ионов об электроны ввиду малой'массы последних несущественно, и более важную роль играет вязкость, вызываемая соударениями ионов друг с другом: г. а = — (д1дхр) Л;,ар. В дальнейшем нам понадобятся
Следующие значения компонент тензора вязкости: — тсуу =
= — Г)! (Шхх — УУуу) 2г)3й^х!/) ЛХ1/ — лу* ^ 41^ ху ~2 ( ^хх
-Жуу),где
Ш иг — — Ш — до* I д“у
Уухх - и Уи — 1 ^ ах ду). ууху - Эу + дх,
П „ пТ;1 „ р. с пТI
(см., например,16). Здесь и в дальнейшем используется декартова система координат, ось Ог которой направлена вдоль магнитного поля, Ох — вдоль градиента плотности плазмы.
Хотя поведение полностью ионизованной и слабо ионизованной плазмы описывается сходными уравнениями, их физический смысл не вполне одинаков. Гидродинамическая система уравнений для полностью иониэо- .ванной плазмы выводится посредством регулярной процедуры из кинети
ческого уравнения (см., например,10). Эта процедура основана на том, что вид функции распределения каждой из компонент плазмы определяется в основном соударениями между одинаковыми частицами (электрон-элек - тронными и ион-ионными). Под действием соударений устанавливается максвелловское распределение, параметрами которого являются плотность, скорость и температура. Гидродинамические уравнения определяют эволюцию этих параметров. В плазме слабо ионизованной функция распределения заряженных частиц определяется внешними электрическими полями, поддерживающими разряд, и соударениями с нейтралами. Поэтому энергия и скорость каждой из компонент однозначно определены и соответственно гидродинамическая система уравнений сводится к единственному уравнению для плотности 17>18. Область применимости такой модифицированной гидродинамики довольно ограничена, и поэтому приходится использовать моменты кинетического уравнения, которые имеют смысл уравнений баланса. Обрыв системы моментов может привести к значительным погрешностям при рассмотрении процессов, в которых существенную роль играют высшие моменты. К счастью, дрейфово-диссипативная неустойчивость обязана такому грубому отклонению от состояния термодинамического равновесия, как градиент плойюсти. Поэтому ее развитие с достаточной точностью описывается двумя первыми моментами кинетического уравнения (см., однако, гл. 4 настоящего обзора).
Рассмотрим с помощью (1.2) движение электронов поперек магнитного поля в отсутствие колебаний. Предположим, что в начальном состоянии нет электрического поля. Считая также, что Р±е= 0 (см. выше), получаем следующее выражение для скорости электронов в направлении поперек магнитного поля:
|
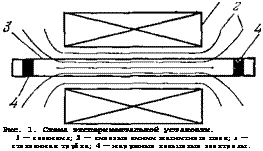
Рис. 1. Схема экспериментальной установки. 1 — соленоид; 2 — силовые линии магнитного поля; з — стеклянная трубка; 4 — наружные кольцевые электроды. |
 Из (1.4) следует, что если плотность плазмы меняется в направлении поперек магнитного поля, то ее электронная компонента находится в состоянии движения. Такое движение называется градиентным или ларморовским дрейфом. Оно интересно тем, что гидродинамическая макроскопическая скорость не связана с перемещениями отдельных электронов, каждый из которых в среднем покоится, вращаясь по неподвижной лар - моровской окружности 15.19.
Из (1.4) следует, что если плотность плазмы меняется в направлении поперек магнитного поля, то ее электронная компонента находится в состоянии движения. Такое движение называется градиентным или ларморовским дрейфом. Оно интересно тем, что гидродинамическая макроскопическая скорость не связана с перемещениями отдельных электронов, каждый из которых в среднем покоится, вращаясь по неподвижной лар - моровской окружности 15.19.
Б) Дрейфовые колебания
Приступим к рассмотрению колебаний неоднородной плазмы в магнитном поле. Прежде всего проанализируем их пространственную зависимость. Она определяется геометрией системы. Обычно дрейфовые колебания изучаются в системах, имеющих форму сильно вытянутого цилиндра, длина которого на один-два порядка превышает диаметр. Магнитное поле создается коаксиальными катушками и направлено параллельно оси системы. Типичная экспериментальная установка, использовавшаяся для изучения колебаний газоразрядной плазмы в магнитном поле, изображена на рис. 1.
Поскольку параметры плазмы слабо меняются вдоль оси, система в этом направлении может приближенно считаться однородной. Наибольшую трудность представляет анализ радиальной зависимости, так как для этого приходится решать систему дифференциальных уравнений с переменными коэффициентами. Однако оказывается, что в интересующих нас колебаниях из всех радиальных движений плазмы наиболее существенную роль играет дрейф в скрещенных полях: постоянном аксиальном магнитном поле и азимутальном электрическом поле колебаний. Такой дрейф приводит к смещениям плазмы по радиусу, т. е. в направлении градиента плотности, что и вызывает колебания плотности. Для учета этого эффекта достаточно рассмотреть возмущения, бегущие по азимуту и не зависящие от радиуса. Детальный анализ проблемы подтверждает законность такого подхода (см., например,3-6'8-11). Поскольку радиальная зависимость возмущений оказалась несущественной, то вместо аксиально-симметричной системы можно рассматривать систему с плоской симметрией. (Направление вдоль Ох эквивалентно радиальному, вдоль Оу — азимутальному). С учетом всего сказанного выражения для возмущений плотности и потенциала в колебаниях принимают вид ~ exp (—ioit + ikzz 4- ikyy) [45])■ Сделаем дополнительно следующие упрощения: положим Т-, = 0; пренебрежем движением ионов вдоль магнитного поля (см. выше), а их поперечное движение будем считать бесстолкновительным FI = 0. Предполагая также, что частота колебаний не слишком велика, в ионном уравнении движения опустим силу инерции. При этих предположениях из (1.2), (1.3) находим
![]()
|
У|И = 0, |
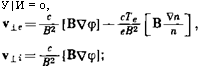 (1.5)
(1.5)
(1.5) (1.7)
(1.8)
Здесь Ье = е1тее, Бе = Те/тее — коэффициенты подвижности и диффузии электронов соответственно.
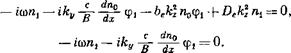 Подставляя (1.5) — (1.8) в уравнения непрерывности и линеаризуя их по малым возмущениям плотности п0 и потенциала фх, получаем
Подставляя (1.5) — (1.8) в уравнения непрерывности и линеаризуя их по малым возмущениям плотности п0 и потенциала фх, получаем
(1.9)
(1.10)
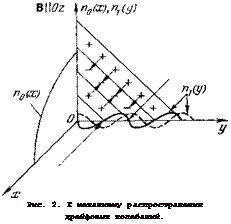
Наряду с анализом уравнений (1.9), (1.10) попробуем, следуя 23, наглядно представить механизм распространения колебаний. Для этого обратимся к рис. 2. На нем представлено мгновенное распределение плотности в волне ~ exp (—i(ot + ikyy ikzz), области повышенной плотности отмечены знаком «плюс». Уравнения (1.9), (1.10) совместны,
если два последних слагаемых в (1.9) взаимно сокращаются. Это означает, что градиент давления электронной компоненты компенсируется электрическим полем ф! = (Ое! Ъе) п1/п0 = (Те/е) /г1/и0. Поэтому области повышенной концентрации должны быть заряжены положительно. На рис. 2 направление электрического поля показано короткими стрелками. Поскольку электрическое поле имеет «/-компоненту, плазма дрейфует по Ох (длинные стрелки). В область справа от максимума приходит плазма из более глубоких слоев, где ее плотность больше (на рис. 2 плотность спадает по Ох). В область слева от максимума приходит плазма из слоев, расположенных ближе к поверхности, где плотность плазмы имеет меньшее значение. В результате вся картина смещается вправо (пунктирная кривая). Непрерывное повторение этого процесса означает, что по плазме бежит волна плотности и потенциала. Эта волна не нарастает и не затухает (1шсо =0). Действительная часть, как следует из (1.9), (1.10), равна со[46] = к,, х сТе! еВ, где х =
|
Рис. 2. К механизму распространения дрейфовых колебаний. |
|
Области повышенной концентрации в волне обозначены знаком плюс, пониженной — минус. Синусоидами представлены мгновенные распределения плотности плазмы гц (у) в волне. Направление дрейфа заряженных частиц в волне показано длинными стрелками, электрического поля волны — короткими. |
 = —(1 /п0)<1п0/йх. Эта частота называется дрейфовой и соответственно сами колебания дрейфовыми. Дрейфовые колебания были впервые рассмотрены в работе 24 на примере полностью ионизованной плазмы. Дальнейшее развитие теории дрейфовых колебаний отражено в обзорных работах
= —(1 /п0)<1п0/йх. Эта частота называется дрейфовой и соответственно сами колебания дрейфовыми. Дрейфовые колебания были впервые рассмотрены в работе 24 на примере полностью ионизованной плазмы. Дальнейшее развитие теории дрейфовых колебаний отражено в обзорных работах
В, 9, 11
Остановимся на двух интересных моментах.
1) Дрейфовые колебания не затухают, хотя о).<^ е. Причина этого ясна. Поскольку электроны распределены по закону Больцмана, то их средняя макроскопическая скорость равна нулю, а вместе с ней обращается в нуль и сила трения.
2) Фазовая скорость дрейфовых колебаний в направлении ОУ оказалась равной невозмущенной скорости ларморовского дрейфа электронов (1.4). Поэтому на первый взгляд, создается впечатление, что здесь мы имеем дело с переносом возмущений электронным потоком. Однако поскольку при ларморовском дрейфе каждый отдельный электрон н среднем покоится, такой перенос, очевидным образом, невозможен. Лармо - ровский дрейф вообще не может привести к изменению плотности, и поэтому соответствующее слагаемое V («V*) выпадает из результирующего уравнения непрерывности (1.9). По-видимому, совпадение фазовой скорости колебаний со скоростью ларморовского дрейфа вызвано тем, что последняя является простейшей величиной с размерностью скорости, характеризующей неоднородную плазму в магнитном поле. Действительно, поскольку макроскопическую скорость можно считать мерой неравно - весности плазмы, то естественно предположить, что она должна быть пропорциональна х Т. Простейшая комбинация из величин х7 е, В, с, /та,, тпе *), имеющая размерность скорости, очевидно, совпадает со скоростью ларморовского дрейфа (сТ/еВ) х (сравнить с (1.4)).
Дрейфовые колебания не затухают и не нарастают (1хгко = 0). В определенном смысле можно утверждать, что плазма с дрейфовыми колебаниями представляет собой новый тип равновесного состояния. Поскольку в дрейфовых колебаниях «грубые» силы (давление и сила со стороны электрического поля) уравновешиваются, решающими могут оказаться более тонкие эффекты. Именно поэтому, например, корректное рассмотрение дрейфовых колебаний в полностью ионизованной плазме в некоторых случаях может потребовать расширения схемы обычной гидродинамики с учетом более высоких моментов функции распределения 6. Мы же в настоящий момент учтем инерцию ионов. Ее влияние оказывается весьма существенным даже при низкой частоте колебаний ш ю;.
С помощью уравнения (1.3) определяем скорость ионов в направлении поперек магнитного поля
Ухп = -^[ВУф1] + -^-^У±Ф1. (1.11)
Движение ионов вдоль магнитного поля по-прежнему не учитываем. Подставляя (1.11) в уравнение неразрывности и принимая во внимание выражение для частоты дрейфовых колебаний (см. предыдущий раздел), находим, что учет силы инерции уменьшает второе слагаемое в (1.10) на множитель (1—йгур? е); здесь Р;е = Те1т1 — ларморовский радиус
Ионов, сосчитанный по электронной температуре. Таким образом, инерция ионов эффективно замедляет дрейф в скрещенных полях, в результате дрейфовое смещение ионов оказывается меньше электронного и амплитуда колебаний электронной плотности превышает ионную. Квазинейтральность плазмы поддерживается за счет перераспределения электронов вдоль магнитного поля. Причем избыточные электроны, переходя из областей с большей плотностью в области с меньшей плотностью, вынуждены совершать работу против электрического поля, см. рис. 2. В результате амплитуда колебаний возрастает. Поскольку энергия отбирается у электронов, они охлаждаются. В конечном счете энергия тратится на то, чтобы привести в движение тяжелые ионы. Эти процессы не противоречат второму началу термодинамики, так как колебания плазмы в направлении градиента плотности сглаживают его величину (среднюю по колебаниям), приближая систему к равновесию.
Какова роль трения электронов о тяжелые частицы в этом механизме раскачки колебаний? Если бы электроны вдоль магнитного поля двигались свободно-инерционно, то, как легко показать, изменение их плотности при движении под действием избыточного давления было бы сдвинуто по фазе относительно первоначального возмущения на я/2. При этом мы получили бы чисто колебательный режим без нарастания первоначальных возмущений. Если смотреть более глубоко, то роль трения состоит, по-видимому, в том, что оно вносит элемент необратимости. В результате процесс сглаживания профиля плотности плазмы в колебаниях приобретает необратимый характер. Это, в конечном счете, и позволяет колебаниям без противоречия со вторым началом термодинамики отбирать тепловую энергию у электронов.
Покажем, что вывод о неустойчивости плазмы следует и из формального анализа. Учет инерции ионов приводит к появлению в (1.10) дополнительного слагаемого — гА:у (с/В) (со/со£) В результате диспер
Сионное уравнение для определения частоты собственных колебаний плазмы, которое получается из условия совместности уравнений (1.9),
(1.10) , приобретает следующий вид:
Ш-ш* = ;^^р? е-соЛ£р? е. (1.12)
Пренебрегая сначала малой правой частью (1.12), которая обязана учету силы инерции, получаем ш = ш* = (сТе! еВ) куу. (см. выше). В следующем приближении находим, что колебания неустойчивы (1та) > 0).
2. ДРЕЙФОВАЯ НЕУСТОЙЧИВОСТЬ В СЛАБО ИОНИЗОВАННОЙ ПЛАЗМЕ ГАЗОВОГО РАЗРЯДА В МАГНИТНОМ ПОЛЕ
А) Обнаружение неустойчивости
Исследования колебаний бестокового газового разряда в магнитном поле ведут свое начало с экспериментов, описанных Бомом (см. введение). Эти эксперименты были продолжены в работах 25_28. Было обнаружено, что аномалии в поведении плазмы проявляются, лишь если магнитное поле превышает некоторое критическое значение ВКр. Причем при В > > Внр иэ области, занятой пучком первичных электронов, вырываются один или несколько плазменных «факелов», вращающихся вокруг пучка. С увеличением магнитного поля появляются факелы различного пространственного масштаба, вращающиеся с различной скоростью. Одновременное присутствие в разряде нескольких факелов приводило к беспорядочной хаотической картине, т. е. к турбулентности.
В работе 29 исследовался высокочастотный разряд в магнитном поле. Здесь была обнаружена аномальная зависимость нагрузки на генератор от магнитного поля. Намного раньше в30 было замечено, что в таком разряде наблюдается аномалия в поведении электронной температуры в магнитном поле, которая возрастала с увеличением поля. Более подробное изучение высокочастотного разряда 31 позволило установить, что при увеличении магнитного поля выше критического возрастает поток положительных ионов поперек магнитного поля и одновременно с этим плазма начинает генерировать высокочастотные электрические колебания, имеющие характер шума. Все эти факты свидетельствовали косвенным образом о возникновении неустойчивости и увеличении коэффициента диффузии.
Естественно было ожидать, что наиболее спокойной окажется распадающаяся плазма, остающаяся в разряде после выключения источника ионизации, так называемая плазма послесвечения. Действительно, в такой плазме, в отличие от плазмы высокочастотного разряда, электронная температура близка к температуре нейтрального газа, а стационарное электрическое поле, которое обычно самопроизвольно возникает в газовом разряде (амбиполярное поле), оказывается довольно слабым. Однако исследования показали, что и в распадающейся плазме коэффициент диффузии имеет аномально большую величину 32- 33. Делались попытки связать аномалию с влиянием примесей, перекосом оси разрядной трубки относительно магнитного поля, рекомбинацией и т. д. (см., например, 34> 35). Эти эффекты были проанализированы в работах 36-38 (см. также 7). Их авторы пришли к выводу, что увеличение коэффициента диффузии может быть обусловлено лишь развитием неустойчивых колебаний.
Аномальная диффузия, сопровождающаяся возбуждением электрических шумов, была обнаружена и в так называемом разряде с осциллирующими электронами 39 > 40.
Б) Первые попытки идентификации неустойчивости
Поскольку сходные явления наблюдались в разрядах различного типа, было естественно предположить, что здесь действует некий универсальный механизм неустойчивости, не связанный с особенностями конкретного вида разряда. Для того чтобы выяснить, не был ли таким механизмом дрейфово-диссипативный, следовало прежде всего найти условия неустойчивости и сравнить их с экспериментальными. Для этого в идеализированную схему, использованную в предыдущем разделе, должны быть дополнительно включены некоторые факторы, проявляющиеся в реальных системах. Для слабо ионизованной плазмы газового разряда такими факторами являются: соударения ионов с нейтралами, конечная величина температуры ионов (71; =5^= 0), ограниченность системы в направлении вдоль магнитного поля и др. В 41 был учтен лишь один из них (соударения ионов с нейтралами). Этот фактор оказался наиболее существенным. Для того чтобы включить в рассмотрение соударения ионов с нейтралами, следует в (1.11) произвести замену а>—► а> IV,-. При этом дисперсионное уравнение для частоты приобретает следующий вид:
Со2 + гш (V; 4- Оек (1 + ку2р^)) -{- Оек? (— га— V,) = 0. (2.1)
При V; = 0 это уравнение, как легко показать, переходит в (1.12).
Анализ (2.1) дает следующие приближенные условия неустойчивости:
|
|
(2.2)
Из (2.2) нетрудно найти, что отдельные моды с фиксированными значениями ку, кг могут раскачиваться лишь в определенных интервалах изменения магнитного поля:
|
|
(2.3)
Область неустойчивости расширяется с увеличением | (уменьшением давления, увеличением градиента плотности плазмы) и уменьшением продольного волнового числа. Области неустойчивости мод с различными значениями ку могут перекрываться, причем для раскачки колебаний с большим ку требуется большее магнитное поле.
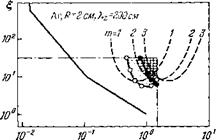
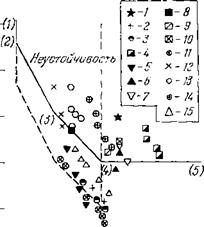
В работе 41 с помощью (2.2) была определена область неустойчивости плазмы н аплоскости £; т) = (й)гЛ>;) = 1/хр,;е. Эти координаты удобно
Использовать для характеристики состояния плазмы, так как они простым образом связаны с давлением нейтрального газа £ ~ р~1 и магнитным полем г ~ В, т. е. величинами, которые наиболее просто менять в эксперименте. Оказалось* что для неустойчивости необходимы достаточно большие значения £ (£ > 1). Это ограничение естественно, так как причиной неустойчивости является неравновесность плазмы, характеризуемая величиной градиента £— х. Более точные расчеты (см. 8> 42) дают
(2.4)
|
|
На рис. 3 эта граница отмечена цифрами (4)—(5). Участок границы (3)—(4) (£т| = да 1) определяется из условия раскачки колебаний с наи -
Именыпим возможным значением ку да х (см. левое неравенство (2.3)). При дальнейшем уменьшении магнитного поля критические значения |
|
10* |
|
10* |
|
Рис. 3. Сплошная линия — границы области дрейфовой неустойчивости, пунктирная — ионно-звуковой 41. 1 — Аг1; г — Нг ‘7; 3 — Не 4 — Н. ,0; 5 — Не, г; б — Не 7 — Нг гг; * — Не 9 — Н, ■' ю — Не 8‘; 11 — Аг“, 12 — Аг вв; 13 — Аг 14 — Аг 5>; 15 — Аг ”. |
|
Продолжают возрастать. На участке (2)—(3) имеем |кр > т] 2УЬ1/Ье. Перестают чувствовать магнитное поле (кре > 1). В работе 41 были также определены границы области дрейфово-дис- Называемая ионно-звуковая неустойчивость (см. гл. 5 настоящей рабо- На рис. 3 видно, что значения параметров т|. при которых на В область дрейфово-дисси- На этом основании утвер- Поскольку частота дрей - Фовых колебаний меньше а);, то в работе 43 высокочастотная часть |
|
103 юг ю’ 10° 70 4 |
|
<Ц |
|
-г. |
|
10 |
|
-г |
|
10 |
|
-1 |
|
Ю |
 |
Ствуют какие-то дополнительные механизмы раскачки колебаний. Законен вопрос — не являются ли эти механизмы более сильными и в области частот со > V*?
Наряду с этим в 10' 47 были высказаны сомнения в законности локального квазиклассического приближения, при использовании которого, несмотря на неоднородность системы, возмущения выбираются в виде плоских волн. Убедительный ответ на все эти вопросы мог быть дан только в результате прямой экспериментальной проверки дисперсионного соотношения (2.1).
В) Выделение отдельных мод неустойчивых
Колебаний
Очевидно, что дисперсионное соотношение можно проверить лишь в том случае, если плазма находится в ламинарном режиме, т. е. в ней возбуждено небольшое число мод колебаний, лучше всего одна. Причем
Амплитуда колебаний должна быть достаточно малой, так чтобы оказались
Справедливыми результаты линейного приближения, использованного при выводе (2.1).
|
А |
![]() По-видимому, впервые отдельные моды дрейфовых колебаний в стол- кновительной плазме были выделены в работе 50, где изучались неустойчивые колебания водородной плазмы высокочастотного разряда в магнитном поле. Результаты анализа спектра колебаний схематически изображены на рис. 4. На нем кроме основной часто
По-видимому, впервые отдельные моды дрейфовых колебаний в стол- кновительной плазме были выделены в работе 50, где изучались неустойчивые колебания водородной плазмы высокочастотного разряда в магнитном поле. Результаты анализа спектра колебаний схематически изображены на рис. 4. На нем кроме основной часто
|
Л_л1 |
![]() Ты а)! = 9,4-104 сек-1 видны также гармоники 0)п = 710)! вплоть до п = 5. Спектрограмма, по существу, представляет разложение Фурье нелинейных колебаний, хорошо скоррелированных
Ты а)! = 9,4-104 сек-1 видны также гармоники 0)п = 710)! вплоть до п = 5. Спектрограмма, по существу, представляет разложение Фурье нелинейных колебаний, хорошо скоррелированных
Ы во времени и пространстве. Эти ко -
„ . „ .. , лебания распространялись как по ази -
Рис. 4. Спектр дрейфовых колеса-
Ний50. муту, так и вдоль магнитного поля.
Поскольку система в направлении вдоль магнитного поля была ограничена, то на первый взгляд следовало ожидать установления стоячих волн. Однако в описываемых экспериментах плазма создавалась на одном конце разрядной трубки. По мере движения вдоль магнитного поля плазма терялась на стенках трубки, и до другого ее конца доходила лишь малая доля заряженных частиц. Резкая неоднородность плазмы, по-видимому, и обусловливала распространение колебаний в направлении вдоль магнитного поля. Была измерена фазовая скорость колебаний. При давлении нейтрального ґаза 2-Ю-3 мм рт. ст. ее проекция на азимутальное направление и направление вдоль магнитного поля оказались равными 2-Ю6- и 2-Ю® см/сек соответственно. Продольная длина волны была равна примерно 100 см, структура колебаний в направлении поперек магнитного поля не исследовалась.
В работе 50 изучалась зависимость частоты колебаний от величины магнитного поля. Оказалось, что в соответствии с (1.2) частота уменьшается с ростом магнитного поля со да ш* = кух сТе! еВ. Было также обнаружено, что частота падает при увеличении давления нейтрального газа.
Хотя в 50 и были получены интересные результаты, они не могут считаться полноценной проверкой дисперсионного соотношения ввиду следующего. 1) Не было измерено азимутальное волновое число тп.
2) Производилось сравнение с асимптотическим значением частоты дрейфовых колебаний со[47], которое приближенно справедливо лишь вдали от границы области неустойчивости. 3) Не было проанализировано влияние неоднородности плазменного столба в направлении вдоль магнитного поля. 4) Полученные данные относятся к нелинейному режиму, о чем говорит наличие в спектре колебаний большого числа гармоник основной частоты.
В 61 отдельные моды колебаний исследовались в однородном в направлении вдоль магнитного поля столбе плазмы высокочастотного разряда. Было показано, что колебания, как и требовалось по теории, бежали по азимуту в электронную сторону, а их частота по порядку величины равнялась дрейфовой. На плоскости £ — т} (см. рис. 3) неустойчивому состоянию плазмы соответствовала область, лежащая внутри области дрейфовой неустойчивости, ограниченной линиями 1—5.
Отдельные моды колебаний были выделены также в плазме отражательного разряда в магнитном поле. Интересующий нас столкновительный режим изучался в работе 52 *). Было показано, что частота колебаний по порядку величины совпадает с рассчитанной из (2.1).
Делались также попытки обнаружить дрейфовые колебания в разряде постоянного тока в магнитном поле 56“58. Однако в силу сравнительно низких частот дрейфовых колебаний их характеристики могли существенно модифицироваться в результате направленного движения электронов. (Разряд постоянного тока более благоприятен для исследования ионно-звуковых колебаний с со со*, см. гл. 5.) Возможно, что именно по этой причине колебания, обнаруженные в 5в, бежали по азимуту в ионную сторону, а колебания, исследовавшиеся в 58, где они были названы лсевдоионно-циклотронными, образовали волну, бегущую вдоль магнитного поля.
Г) Проверка дисперсионного соотношения
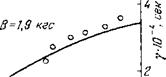
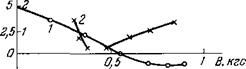
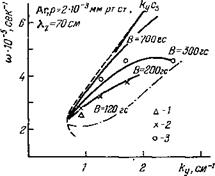
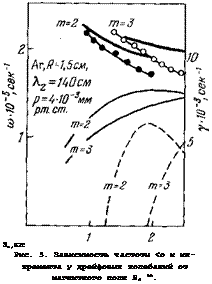
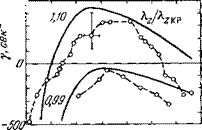
Подробное изучение дрейфовых колебаний в плазме высокочастотного разряда в магнитном поле было проведено в работах 59~64. В 63 исследовалась зависимость частоты колебаний с азимутальными волновыми числами = 2; 3 от магнитного поля. На рис. 5 экспериментальные данные нанесены кружками. На нем приведены также результаты расчетов по (2.1) действительной части частоты (сплошные линии) и мнимой (штриховые). На рисунке приведена лишь та часть зависимости со от В, которая соответствует неустойчивости плазмы (у > 0). Область изменения магнитного поля на рис. 5 ограничена максимальным значением 2,5 кгс, достигнутым в экспериментах 63.
Из рис. 5 видно, что в плазме, как это и следует из теории, область неустойчивости ограничена как со стороны малых, так и со стороны больших магнитных полей, причем колебания на опыте обнаруживаются внутри рассчитанной области. С увеличением магнитного поля первыми раскачиваются колебания с меньшим номером т. При больших магнитных полях, также в соответствии с теорией, в некоторой области изменения магнитного поля В в плазме одновременно возбуждаются колебания с различными значениями т (т = 2 и 3). В 63 действительная часть часто
ты рассчитывалась как с учетом радиального электрического поля, так и без него (соответственно толстые и тонкие кривые). Радиальное поле приводит к вращению плазмы и из-за эффекта Допплера к изменению частоты дрейфовых колебаний. Использование значений радиального поля, найденных на эксперименте, приводит, как видно из рис. 5, к достаточно хорошему согласию между теорией и экспериментом (сравни сплошные толстые линии и линии с кружками).
|
Аг, р — 4»10“* мм рт. ст., Хг = 140 сж. Кружки |иО соответствуют азимутальным волновым числам т = 2 и 3, Толстые сплошные линии — расчетные значения частот с учетом эффекта Допплера, тонкие — без учета этого эффекта. Штриховые кривые —расчетные значения инкрементов. |
|
За, кгс Рис. 5. Зависимость частоты <о и инкремента у дрейфовых колебаний от магнитного поля В0 вз. |
 В 64 изучалась зависимость частоты колебаний от проекции волнового вектора на направление магнитного поля кх. Характерная зависимость со от кг представлена на рис. 6. Из рисунка видно, что экспериментальные данные, отмеченные кружками, находятся в хорошем согласии с расчетными, полученными с учетом радиального электрического поля. На том же рисунке штриховой линией проведена расчетная зависимость инкремента у от кг (показана часть кривой с - у > 0). Область неустойчивости ограничена как со стороны малых, так и со стороны больших длин волн, что и имело место на эксперименте. Поскольку в плазме вдоль магнитного поля укладывается не менее чем половина длины волны (кг ^ я/£-), то из рис. 6 следует, что дрейфовые колебания могут раскачиваться в плазме лишь в том случае, если ее протяженность превышает некоторый минимальный размер, определяемый параметрами разряда и радиусом трубки.
В 64 изучалась зависимость частоты колебаний от проекции волнового вектора на направление магнитного поля кх. Характерная зависимость со от кг представлена на рис. 6. Из рисунка видно, что экспериментальные данные, отмеченные кружками, находятся в хорошем согласии с расчетными, полученными с учетом радиального электрического поля. На том же рисунке штриховой линией проведена расчетная зависимость инкремента у от кг (показана часть кривой с - у > 0). Область неустойчивости ограничена как со стороны малых, так и со стороны больших длин волн, что и имело место на эксперименте. Поскольку в плазме вдоль магнитного поля укладывается не менее чем половина длины волны (кг ^ я/£-), то из рис. 6 следует, что дрейфовые колебания могут раскачиваться в плазме лишь в том случае, если ее протяженность превышает некоторый минимальный размер, определяемый параметрами разряда и радиусом трубки.
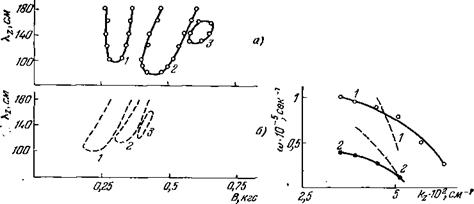
В 63 проверялись области раскачки дрейфовых колебаний на плоскости г), рассчитанные в 41. На рис. 7 светлыми и темными кружками представлены границы области неустойчивости отдельных мод колебаний, полученные на опыте. Области раскачки колебаний с т = 2 (светлые кружки) обозначены горизонтальной штриховкой, а с т = 3 (темные кружки) — вертикальной. Штрих-пунктирными линиями на рис. 7 ограничена исследованная в работе 63 область значений параметров £ и т|. Из рис. 7 видно, что область неустойчивости отдельных мод колебаний располагается внутри предсказанной теорией области изменения параметров ^ и т], однако занимает лишь часть ее. При расчетах в 41 считалось, что температура ионов в плазме Г* = 0. Учет того обстоятельства, что Гг =5^ 0, как было показано в 59, может сократить область неустойчивости. Действительно, дрейфовые колебания возможны, если ларморов - ский радиус ионов рг < х-1, что при Т; г» 0,01 Те приводит к условию г|>0,1. Если использовать это условие, то область неустойчивости сокращается со стороны малых магнитных полей. Однако и после этой коррекции расхождение между теорией и экспериментом, как видно из рис. 7, все еще остается. Обнаруживается также и расхождение в соответствующих границах со стороны малых значений £ (высоких давлений газа). Лучшее согласие между опытными и расчетными значениями получается при учете конечной длины системы вдоль направления магнитного поля, приводящем к ограниченности величины к2 (кг ^ я! Ь) Рассчитанные для
конкретного значения кг области неустойчивости колебаний трех первых азимутальных мод изображены на рис. 7 штрихом. (Полная область неустойчивости представляет собой сумму областей отдельных мод колебаний при Тошах - V оо.) Из рис. 7 видно, что найденные таким образом нижние по
|
О |
![]()
|
ОШ |
![]()
|
Агг Я=1 САН, р=4 Ю~3трт. ст,
|
Мг, см 1
Рис. 6. Зависимость частоты и и инкремента у дрейфовых колебаний от проекции волнового вектора на направление магнитного поля (кг = 2л/кг) 64. Аг, р = 4'10"3 мм рт. ст., т = 2, В — 1,9 кгс. Штриховал кривая—расчетные значения инкрементов.
|
Рис. 7. Область дрейфовой неустойчивости €4. |
Кружки О и | соответствуют} азимутальным волновым числам т — 2 и 3. Штриховыми линиями обозначены расчетные области раскачки колебаний с тп = 1,2 и 3. Штрих-пунктирными линиями ограничена исследованная в работе область.
|
В, гс |
![]()
|
Рис. 8. Зависимость азимутального номера моды неустойчивых колебаний т от магнитного но |
![]() Ь и т] границы области неустойчивости отдельных мод колебаний достаточно хорошо совпадают с установленными на опыте. В то же время следует отметить, что первая мода колебаний, которая согласно теории должна раскачиваться при наименьших магнитных полях, на опыте не наблюдалась.
Ь и т] границы области неустойчивости отдельных мод колебаний достаточно хорошо совпадают с установленными на опыте. В то же время следует отметить, что первая мода колебаний, которая согласно теории должна раскачиваться при наименьших магнитных полях, на опыте не наблюдалась.
|
Не, р = 2,2* 10“* .мм рт. ст. |
|
65 |
![]()
|
Ля |
![]() Характеристики отдельных мод дрейфовых колебаний исследовались также в плазме отражательного разряда в магнитном поле 65. При интерпретации экспериментальных данных предполагалось, что в плазме должны устанавливаться колебания, инкремент которых максимален. Из (2.1) следует, что для этого компоненты волнового вектора к2 и ки должны удовлетворять соотношению 0)* = 0)8, где (08 =
Характеристики отдельных мод дрейфовых колебаний исследовались также в плазме отражательного разряда в магнитном поле 65. При интерпретации экспериментальных данных предполагалось, что в плазме должны устанавливаться колебания, инкремент которых максимален. Из (2.1) следует, что для этого компоненты волнового вектора к2 и ки должны удовлетворять соотношению 0)* = 0)8, где (08 =
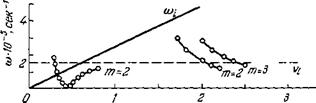
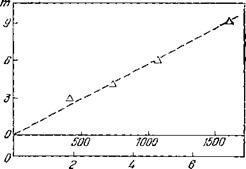
= АЛг (кир1е)-2. При дрейфовой неустойчивости, как правило, раскачиваются длинноволновые моды с небольшим числом узлов. Поэтому при изменении магнитного поля, давления нейтрального газа и т. д. перестройка мод должна происходить дискретно через довольно большие интервалы изменения этих параметров. В таких условиях упрощенный эквивалент дисперсионного соотношения В виде (О* = (05 может быть проверен лишь в отдельных точках. В то же время были получены 65 интересные данные, касающиеся перестройки азимутальных мод (рис. 8). Из итого рисунка следует, что увеличение
магнитного поля приводит к возрастанию азимутального волнового числа неустойчивых колебаний, причем в соответствии с левым приближенным неравенством (2.3) т-я мода неустойчива при aij/Vj » т. « ку/х.
Необходимо особо остановиться на экспериментах 2а-66 ■ 67, где исследовались колебания плазмы высокочастотного разряда и плазмы послесвечения в магнитном поле. Были выделены отдельные моды колебаний, идентифицированных как дрейфовые, и проверен закон дисперсии. Было обнаружено хорошее соответствие с теоретическими расчетами. Однако оказалось, что частота колебаний может принимать значения существенно меньшие (на порядок величины) частоты соударений ионов с нейтралами. Этот результат противоречит основным положениям теории дрейфовой неустойчивости.
В экспериментах с плазмой послесвечения 22'6в изучалась поздняя стадия разряда, когда плотность плазмы была довольно низка. Поэтому можно предположить, что на самом деле в этих работах наблюдался низкочастотный вариант дрейфово-диссипативной неустойчивости разреженной плазмы (см. раздел гл. 4 настоящего обзора). Согласие с теорией дрейфовой неустойчивости можно попытаться приписать тому обстоятельству, что в 22’ 66 при теоретических расчетах дополнительно вводилась зависимость возмущений от координаты х по закону e'h*x. При этом, как отмечено в примечании на стр. 278, мог быть искусственно введен дополнительный эффект раскачки, что, по-видимому, и привело к выводу о неустойчивости дрейфовых колебаний с ш v;.
3. ДРЕЙФОВАЯ НЕУСТОЙЧИВОСТЬ В ПОЛНОСТЬЮ ИОНИЗОВАННОЙ
ПЛАЗМЕ (?-МАШИН
Обычно для ионизации газа используются электрические поля или пучки быстрых частиц. Получающаяся таким образом плазма оказывается в состоянии, весьма далеком от термодинамического равновесия и, следовательно, потенциально неустойчивом, ^-машины были задуманы как устройства со спокойной (quiescent) полностью ионизованной плазмой. В них плазма создается термической ионизацией пучка нейтральных атомов, падающих на накаленную металлическую пластину. После образования плазма свободно вытекает с пластины вдоль магнитного поля. Однако даже такая «спокойная» плазма преподнесла достаточное количество сюрпризов. В частности, в ней было зафиксировано развитие нескольких типов неустойчивостей. Понадобилось известное время для того, чтобы разобраться в наблюдаемых явлениях, а из числа неустойчивостей выделить дрейфово-диссипативную. Мы не будем останавливаться на этом первоначальном этапе исследований, который достаточно полно освещен в ев, 69 Перейдем сразу к выводу и проверке дисперсионного соотношения дрейфово-диссипативной неустойчивости (см. 7°-72).
В плазме (?-машин ионная температура близка к электронной. При рассмотрении колебаний в такой плазме в ионном уравнении движения необходимо учитывать давление и вязкость. В компоненты тензора вязких напряжений, приведенные в гл. 2, входят два коэффициента вязкости - Г)! = 0,3 nTtvj/cof и Т}3 = 0,5 nT-Jdii. Слагаемые, пропорциональные т]3, учитывают так называемую бесстолкновительную вязкость, обязанную эффектам конечного ларморовского радиуса, а пропорциональные столкновительную вязкость. Использование гидродинамического приближения предполагает, что частота рассматриваемых процессов мала по сравнению с частотой ионных соударений а)<^ vt. Ниже мы увидим, что такие колебания могут быть неустойчивыми. В этом пункте мы имеем коренное различие между плазмой полностью ионизованной и слабо
Ионизованной. Дело в том, что в плазме слабо ионизованной соударения ионов с нейтральными атомами приводят не к выравниванию градиентов скорости (вязкость), а к торможению ионной компоненты (трение). Трение оказывает существенно более сильное стабилизирующее воздействие. Именно поэтому колебания с со ^ V,- в слабо ионизованной плазме оказываются устойчивыми (см. предыдущую главу).
При выводе дисперсионного соотношения дрейфовых колебаний, как и в гл. 1, пренебрежем смещениями ионов вдоль магнитного поля. Используя ионное уравнение движения (1.3) и уравнение непрерывности, получаем
— шщ + ikyY, п0ц>1 + — ш + (kyPj)1] ( Иоф, + — щ ) = 0. (3.1)
Дисперсионное уравнение, которое определяется из условия совместности (1.9), (3.1), удобно представить в следующем виде:
((0 __ m.) (1 _ «L ) = t JL. {kyPi)2 (ft) + m.) _ 2iQi - 2o) (V,.)2- (3.2)
Здесь для кратности введены обозначения Qe = DJtl, Q( = 0,3 v(- (куР;)1. Если в (3.2) пренебречь столкновительной вязкостью, положив = 0, то различие между (1.12) и (3.2) будет обязано лишь эффектам конечного ларморовского радиуса (бесстолкновительная вязкость). При (А^рг)2 1
Правая часть (3.2) как и в разделе в) гл. 1 может быть учтена в качестве малой поправки. В нулевом приближении по Arypf имеем ш = ш*. Подставляя это значение частоты в правую часть (3.2), находим, что она равна удвоенной правой части (1.12), следовательно, возрастает вдвое и инкремент колебаний. Это означает, что в изотермической плазме эффекты конечного ларморовского радиуса оказывают на дрейфовые колебания точно такое же воздействие, как и инерционные эффекты. Инерция приводила к эффективному замедлению движения ионов в колебаниях (см. гл. 1), таким же согласно 3 должно быть воздействие эффектов конечного ларморовского радиуса. Дело в том, что на заряженные частицы, вращающиеся по ларморовской окружности конечного радиуса, действует в среднем меньшее электрическое поле £3фф = Е (1 — Агур?) 73. В силу эквивалентности инерционных эффектов и эффектов конечного ларморовского радиуса в плазме с горячими ионами могут оказаться неустойчивыми даже колебания с очень низкой частотой, на развитие которых инерционные эффекты не оказывают никакого влияния.
Учтем теперь столкновительную вязкость. Из (3.2) следует, что колебания устойчивы как при очень малых, так и при очень больших значениях йе. Интервал значений, в котором плазма неустойчива, определяется неравенствами (co*A:upi)2^71 > Qe > &г. Последнее неравенство для дальнейшего удобно представить в виде (см. 71)
А > (1,2)1/41 (|^)1/2 (Tmw)'* ~ (-^)1/2TO?'V,/2. (3.3)
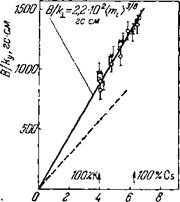
Зависимость критического магнитного поля от массы ионов удобно проверять, используя плазму, образованную из смеси двух элементов. Среднюю массу, входящую в выражение для критического магнитного поля, можно менять непрерывно вместе с относительной долей элементов <"*г) = 'Ј)n0amij'^n0a. В1 экспериментах 71 использовалась смесь Cs
CL GC
И К. Рис. 9 показывает, что требуемая зависимость В ~ {ть)3/* действительно имеет место. В то же время коэффициент пропорциональности
7 УФН, т. 118, вып. 2
|
3/8 |
|
Ге-см при хг = Т = 2800 °К, п0 = 10“ см-3 ”. Штриховая линия — расчет V '■ |
|
Теория дает В/к = 1,5- І02 <тг> |
|
|
|
|
|
|
|
|
Необходимым учет другого важного стабилизирующего фактора — продольного движения ионов 72, 72 [48]). Заметим, что, в частности, для того чтобы устранить влияние последнего фактора во всех теоретических работах, посвященных исследованию дрейфово-диссипативной неустойчивости, рассматривались колебания, сильно вытянутые вдоль магнитного поля. В работе 72 был рассчитан инкремент дрейфово-диссипативной неустойчивости при учете продольного движения ионов (рис. 10). Из него видно, что колебания с < Яг кр устойчивы при любых значениях магнитного поля. Если Хг > Я2 цР, то в некотором интервале изменения магнитного поля колебания становятся неустойчивыми. Обычно в экспериментальных работах, посвященных изучению дрейфово-диссипативной неустойчивости, приводятся данные лишь о действительной части частоты колебаний. В работе 73 был измерен также и их инкремент. Результаты измерений, как
Следует из рис. 10, хорошо согласуются с теоретическими расчетами,
Если учесть, что кх^= 0, и принять к у = У кх -1- кЦ = 2,5 ку.
На рис. 10 по оси абсцисс отложена величина (В/к±)/(В/к^[ф). На основании этого рисунка можно заключить, что для колебаний с большим значением азимутального волнового числа тп область неустойчивости должна быть сдвинута в сторону больших значений магнитного поля. Эта особенность отражена на рис. 11. Напомним, что то же самое явление имеет место и в слабо ионизованной плазме, см. предыдущий раздел. В работе '2 было найдено, что частота неустойчивых колебаний приближенно равна а)*/2. Этот теоретический результат удовлётворительно согласуется с экспериментальными данными (см. рис. 11).
Для того, чтобы составить представление об условиях, в которых могут проявиться различные стабилизирующие механизмы, полезно обратиться к плоскости (В/кх) (рис. 12). На нем область неустойчивости
Ограничена с трех сторон. Снизу, т. е. в области слабых магнитных полей,
|
£ Э" Г І |
|
• - ГГ,=2 О - /77= 3 А - --- расчет |
|
О |
 |
|
|
|
|
|
|
|
![]()
|
2,5 |
![]()
Рис. 11. Сравнение частоты неустойчивых колебаний с дрейфовой частотой в калиевой плазме п.
При сравнении учтен допплеровский сдвиг.
Рис. 12. Зависимость критической, величины В1к± от кг 72.
1, Т = 2Ь50 °К, п ;
"у
= 2 • 1011 ж-*, х = 1,8 с.«-1. Сплошная линия — расчет.
Стабилизация обязана вязкости, сверху — влиянию продольного движения ионов, наконец, слева, т. е. в области малых длин волн, к стабилизации принодит диффузия электронов. Действительно, как показано в 72 (см. также предыдущий раздел), при достаточно малой длине волны дрейфово-диссипативная неустойчивость стабилизируется даже, если не учитывать продольное движение ионов.
В настоящем обзоре мы привели лишь те результаты, из числа полученных в работах 71- 72, которые нам показались наиболее важными и интересными. Кроме того, там были исследованы следующие зависимости: частоты и инкремента от продольной длины волны, критического магнитного поля от плотности плазмы, частоты колебаний от температуры плазмы, поперечной длины волны от магнитного поля, а также измерен поток плазмы наружу, вызываемый неустойчивыми колебаниями. Вся совокупность результатов 71- 72 не оставляет сомнений в том, что наблюдаемая неустойчивость действительно является дрейфово-диссипативной неустойчивостью и что ее свойства вполне удовлетворительно описываются в рамках используемой теоретической модели. Нам кажется, что именно в экспериментах на ^-машинах теория дрейфово-диссипативной неустойчивости прошла наиболее полную и всестороннюю проверку. В то же время нельзя не отметить численных расхождений между теорией и экспериментом (см. рис. 9, 10). Возможные причины этих расхождений мы уже обсуждали выше.
4. НИЗКОЧАСТОТНАЯ ДРЕЙФОВАЯ НЕУСТОЙЧИВОСТЬ СЛАБО ИОНИЗОВАННОЙ ПЛАЗМЫ В МАГНИТНОМ ПОЛЕ
А) Неустойчивость не полностью замагниченной плазмы
Как отмечалось выше, в ряде экспериментов наблюдались низкочастотные (со Уг) колебания, возбуждение которых невозможно связать с действием механизма неустойчивости, рассмотренного в первом разделе. К настоящему времени удалось разобраться лишь в некоторых из этих экспериментов. Наибольшая ясность достигнута, по-видимому, в понимании природы неустойчивости, наблюдавшейся в работах 77 • 78. При изменении магнитного поля последовательно возбуждались колебания двух Типов. Частота колебаний, возбуждавшихся при сравнительно больших значениях магнитного поля, превышала V* (рис. 13). Соответствующая неустойчивость была идентифицирована как дрейфовая. В области малых магнитных полей наблюдались низкочастотные колебания с ш < vг. Эти колебания, как и дрейфовые, имели вид стоячей волны в направлении
|
В, иге Рис. 13. Зависимость частоты со неустойчивых колебаний от магнитного поля В 5в. Аг, р '= 1-10-* ли рт. ст. Прямой лйнией, проходящей через начало координат, обозначена ионная циклотронная частота. Штриховой линией отмечена частота ион-нейтралъных столкновений |
Вдоль магнитного поля (Ог) и бегущей по азимуту. Характерно, что азимутальная фазовая скорость при некотором значении магнитного поля меняла знак. На левой (падающей части кривой частота — магнитное поле) колебания бежали в электронную сторону, на правой (растущей) в ионную. Длина воны в направлении вдоль магнитного поля была равна удвоенной длине соленоида, так что в плазме укладывалась половина длины волны. Низкочастотные колебания наблюдались лишь в плазме с тяжелыми ионами (Аг, Кг, Хе), причем при таких значениях магнитного поля, когда ларморовский радиус ионов (р( ~ У тг) по порядку величины был сравним с радиусом разрядной трубки. Это обстоятельство натолкнуло на мысль о важной роли эффектов конечного ларморовского радиуса ионов в механизме, раскачки колебаний 79. Влияние эффектов конечного ларморовского радиуса на дрейфовые колебания рассматривалось в предыдущем разделе, однако мы не можем использовать эти результаты. Дело в том, что они были получены с использованием гидродинамического приближения, между тем в случае слабо ионизованной плазмы система гидродинамических уравнений представляет собой совокупность моментов кинетического уравнения (см. гл. 1). Ее использование для описания тонких эффектов, таких как эффекты конечного ларморовского радиуса, потребовало бы дополнительного введения большого числа моментов. В этом случае проще непосредственно обратиться к кинетическому уравнению
^ С, ? / р 1 г Т»л д/ 01 / А ' //. Ч
Здесь / — функция распределения ионов. В работе 79 столкновительный член был взят в модельной форме, учитывающей сохранение числа ионов при столкновениях с нейтральными атомами (см. 80):
|
(4.2) |
![]() St(/)= — v, (/— /o) + v,-jЈ - j dx (/ — /о).
St(/)= — v, (/— /o) + v,-jЈ - j dx (/ — /о).
В (4.2) предполагается, что соударения приводят ионную компоненту в тепловое равновесие с нейтральной /-v /0 = п0 (wi,-/2n7,i)3/2 *ехр (—mv? l2T;), где Ті берется равной температуре нейтрального газа.
Как и ранее, считаем, что в колебаниях все возмущенные величины меняются по закону ехр (—шЬ + ikyy + ik2z). Для определения возмущенной функции распределения /х, кинетическое уравнение (4.1) линеаризуем по малым возмущениям. Интегрируя выражение для Д по скоростям, находим возмущение плотности ионов п1. Выражение для щ по аналогии с (1.9) удобно представить в следующем виде:
|
|
Здесь и = с/В с1ц>а/с1х, ф0 — невозмущенный электрический потенциал, который обычно присутствует в плазме газового разряда и который, вообще говоря, необходимо учитывать при анализе устойчивости.
Соответственно уравнение (1.9) должно быть дополнено слагаемым —Ькуищ. Эффекты конечного ларморовского радиуса учитываются в (4.3) через величины
|
|
|
1 — Ai + A3 d3 —--------- t---- |
|
Oo |
![]()
|
Oo |
![]()
![]()
|
VJ+n2<B* I • |
![]() Где
Где
Tl7,(Zj) = /n(3j)e % Zi = (kyp{)2,
Iп — функция Бесселя от мнимого аргумента.
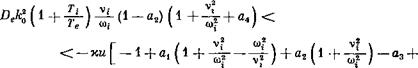
|
Ь>: / Щ i + ~ ala3 “^2“ + ala4 +fl2a4j + |
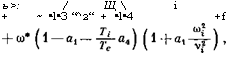 Дисперсионное уравнение для частоты, как обычно, находим из условия разрешимости системы (1.9), (4.3). Его анализ приводит к следующему условию неустойчивости:
Дисперсионное уравнение для частоты, как обычно, находим из условия разрешимости системы (1.9), (4.3). Его анализ приводит к следующему условию неустойчивости:
Где
|
|
Заметим, что хотя величины аг, а2, а3 и не могут превысить единицу, однако сравниваются с ней по порядку величины при &ург да 1.
Из (4.4) следует, что колебания, бегущие по азимуту в ионную сторону (ку <С 0), могут быть неустойчивыми даже в отсутствие электрического
ЛУпв ш-10 5, сек~1
|
Рис. 14. Зависимость величины радиального электрического поля ДУГ (2) и частоты неустойчивых колебаний ь> (2) от магнитного поля В 81. Аг, р — 8-ю-3 мм рт. ст., Х.1 = 120 см, т = 2. -2,5 -5 |
Поля (и = 0). Этот вывод подтверждается измерениями радиального электрического поля, которые были проведены в 81 ( рис. 14). Действительно, мз него видно, что когда электрическое поле обращается в нуль, то не -

|
'1пг А> |
![]() Устойчивы колебания, бегущие в ионную сторону, частота которых возрастает с увеличением В.
Устойчивы колебания, бегущие в ионную сторону, частота которых возрастает с увеличением В.
|
^ сит от соотношения между величи - |
![]() Рассмотрим теперь вопрос о направлении вращения колебаний. Несложные оценки показывают, что в слабо ионизованной плазме знак фазовой скорости дрейфовых колебаний зави -
Рассмотрим теперь вопрос о направлении вращения колебаний. Несложные оценки показывают, что в слабо ионизованной плазме знак фазовой скорости дрейфовых колебаний зави -
|
Б) Ху |
![]() Нами &’е = [к* + к (^/ш?)] и ЗД =
Нами &’е = [к* + к (^/ш?)] и ЗД =
= Ю{{к1 + к1 К2/К+ со?)]}. Если преоб - ладает электронная диффузия
|
(V > о). |
![]() £ то колебания бегут в электронную сторону, если ионная (ЗД > ОД, то в ионную. При достаточно большой длине волны колебаний в направлении вдоль магнитного поля и не слишком малой? температуре ионов может оказаться, (И что при очень малых и очень больших ги значениях магнитного поля выполняется условие ЗД > ЗД, а в промежуточной области — > Яё - В этом слу -
£ то колебания бегут в электронную сторону, если ионная (ЗД > ОД, то в ионную. При достаточно большой длине волны колебаний в направлении вдоль магнитного поля и не слишком малой? температуре ионов может оказаться, (И что при очень малых и очень больших ги значениях магнитного поля выполняется условие ЗД > ЗД, а в промежуточной области — > Яё - В этом слу -
Чае зависимость фазовой скорости от магнитного поля должна иметь следующий вид (рис. 15). Разумеется, на эксперименте будут наблюдаться лишь те части кривой, которые соответствуют положительным инкрементам. На рис. 15 они отмечены жирными линиями (сравнить с рис. 13).
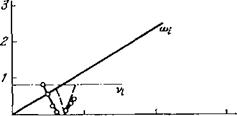
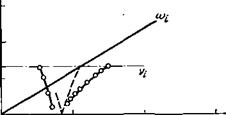
Низкочастотные колебания были подробно изучены в работе 81. На рис. 16 приведены типичные результаты измерений частоты низкочастотных дрейфовых колебаний от магнитного поля, полученные на опыте в слабо ионизованной аргоновой плазме при различных давлениях (кривые с кружками). На том же рисунке штриховыми линиями представлены и рассчитанные с помощью (1.9), (4.3) зависимости частота — магнитное поле. Видно, что между расчетными и опытными данными обнаруживается хорошее соответствие.
|
V 3 § Щ * 3 7 |
|
Рис. 16. Зависимость частоты неустойчивых колебании <о от магнитного ноля В 81. |
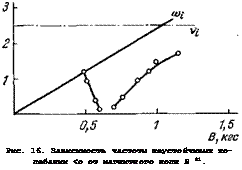
|
Аг, = 180-сл, т = 2; давления (м рт. ст.): 5-10-3 (и), к-К)-3 (б) и 1,5-10-2 (в). Штриховые — расчетные зависимости. |
![]() Теория удовлетворительно передает и характер наблюдаемой экспериментально зависимости частоты колебаний от величины А^-проекции волнового вектора на направление магнитного поля
Теория удовлетворительно передает и характер наблюдаемой экспериментально зависимости частоты колебаний от величины А^-проекции волнового вектора на направление магнитного поля
В. Это видно из рис. 17, где нанесены рассчитанные и измеренные дисперсионные характеристики низкочастотных дрейфовых колебаний •с падающей зависимостью ш от В при Двух значениях магнитного поля. Теория позволяет также определить интервал неустойчивых длин волн в функции от магнитного поля. На рис. 18 изображены найденные на опыте (а) и вычисленные (6) области раскачки колебаний с разными значениями продольной длины волны при трех различных давлениях. Сопоставление приведенных на рисунке данных показывает, что, как и предсказывает теория, низкочастотные дрейфовые колебания в плазме раскачиваются только в ограниченном интервале значений продольных длин волн.
В работах ‘9- 81 проводилось сопоставление измеренных на опыте и рассчитанных областей неустойчивости низкочастотных дрейфовых колебаний по магнитному полю и давлению. Результаты таких сравнений показаны на рис. 19. Видно, что эти области перекрываются лишь частично. Однако обе они располагаются вблизи линии а);/^г = 1. Выполнение последнего условия существенно для раскачки низкочастотных дрейфовых колебаний 77, поскольку необходимое для возникновения этой неустойчивости различие в скоростях дрейфа ионов и электронов в скрещенных ЕукВ ПОЛЯХ особенно велико при (0^; « 1. Заметим, что из условия 0);^; л; 1 можно оценить наименьшее давление, при котором еще возможна неустойчивость. Действительно, с уменьшением давления газа уменьшаются и минимальные значения магнитных полей, необходимых для возникновения неустойчивости в плазме (уменьшение критического магнитного поля). Это, в свою очередь, ведет к росту ионного ларморовского
•радіуса и, когда он превысит радиус разрядной трубки, неустойчивость прекратится. Оценки нижнего предельного давления для существования
|
|
|
Рис. 17. Зависимость продольной длины волны неустойчивых колебаний Хг от магнитного поля В 81. |
|
|
|
Аг, т = 2. а) Эксперимент, давления (мм рт. ст.): 8-10-* (Л), 1,5-10-“ (2) и 3.10-2(3); б) расчет, давления (мм рт. ст.): 5-1о~3 (1), 8-10_г (2) и 1-10—* (3). |
|
Р -]Oj мм рт. ст. |
|
О) |
|
Рис. 18. Зависимость частоты неустойчивых колебаний <о от к, = = 2лДг •*. Аг, р — 8*10-* мм рт. ст., т = 2;т магнитные поля (гсу. 300 (1) и 200 (г). Штриховые — расчетные зависимости. Б) |
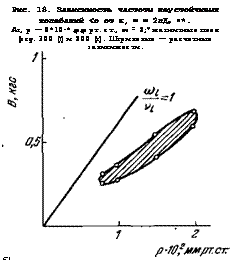 Рис. 19. Области раскачки колебаний по магнитному полю В и давлению р 81.
Рис. 19. Области раскачки колебаний по магнитному полю В и давлению р 81.
Аг, Х.2 = 120 см, т = 2. а) Расчет; б) эксперимент.
Низкочастотной дрейфовой неустойчивости 81 подтверждают правильность - такого подхода.
Б) Неустойчивость разреженной плазмы
Довольно давно в ряде теоретических работ было замечено, что разреженная плазма может оказаться более неустойчивой, чем плотная (см., например, п). Поясним это утверждение. При рассмотрении колебаний в разреженной плазме вместо условия квазинейтральности пе = гег необходимо использовать уравнение Пуассона
Дф = ine (пе — пг). (4.5>
Предполагая, что возмущения плотности электронов в (1.9) и ионов в (1.10) связаны через (4.5), находим следующее дисперсионное уравнение для частоты колебаний:
Со-ы*=-^~кЧге-<>>т. (4.6)
|
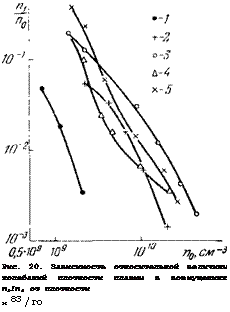
Рис. 20. Зависимость относительной величины колебаний плотности плазмы в возмущениях п11п0 от плотности И 83 /го |
 Это уравнение отличается от (1.12) заменой pie de, где de = YТе/^пегщ — дебаевский радиус электронов. Следовательно, эффекты неквазинейтраль - ности плазмы играют ту же роль, что и инерция ионов, а поэтому в разреженной плазме могут раскачиваться низкочастотные колебания с ш v;. В работах 82' 83 эти воззрения были привлечены для объяснения экспериментов в плазме послесвечения.
Это уравнение отличается от (1.12) заменой pie de, где de = YТе/^пегщ — дебаевский радиус электронов. Следовательно, эффекты неквазинейтраль - ности плазмы играют ту же роль, что и инерция ионов, а поэтому в разреженной плазме могут раскачиваться низкочастотные колебания с ш v;. В работах 82' 83 эти воззрения были привлечены для объяснения экспериментов в плазме послесвечения.
Аномально быстрый распад такой плазмы был отмечен еще ранее 32' 33.
Позднее было обнаружено, что возрастание коэффициента диффузии сопровождается возникновением колебаний 48> 49. Это обстоятельство заставило искать причину аномалий в неустойчивости плазмы. При установлении ее природы необходимо учитывать следующие особенности. 1)
|
2Я — 1,2 см, р == 0.15 мм рт. ст. Магнитные поля (кгс): 0,7 (I), 1 (2), 1,6 (Л), 3 (4) и 5 (5). |
![]() При возникновении неустойчивости безразмерные параметры £, т} лежат вне области дрейфовой неустойчивости на рис. 3 (oijCVj, £<1). 2) Ввиду того, что в плазме послесвечения электронная температура близка к ионной, раскачка ионно-звуковых колебаний в такой плазме невозможна. 3) Неустойчивость развивается лишь на поздних стадиях разряда, когда плотность плазмы оказывается достаточно низкой. Последняя особенность иллюстрируется на рис. 20, взятом из 83, на котором отложена относительная величина флуктуаций плотности плазмы пх1п0 в функции от плотности п0. Аналогичные результаты были получены и при других значениях давления нейтрального газа и радиуса разрядной трубки.
При возникновении неустойчивости безразмерные параметры £, т} лежат вне области дрейфовой неустойчивости на рис. 3 (oijCVj, £<1). 2) Ввиду того, что в плазме послесвечения электронная температура близка к ионной, раскачка ионно-звуковых колебаний в такой плазме невозможна. 3) Неустойчивость развивается лишь на поздних стадиях разряда, когда плотность плазмы оказывается достаточно низкой. Последняя особенность иллюстрируется на рис. 20, взятом из 83, на котором отложена относительная величина флуктуаций плотности плазмы пх1п0 в функции от плотности п0. Аналогичные результаты были получены и при других значениях давления нейтрального газа и радиуса разрядной трубки.
Дисперсионное соотношение (4.6) не может быть использовано для описания этих экспериментов, так как оно получено в предположениях Те Э - ТI, а); v(, в то время как плазма послесвечения почти изотермична
(Те «Гг), а область неустойчивости характеризуется скорее обратным соотношением между частотами а); и vЈ (сог v;). В этом случае несложные вычисления дают
O)(l + s) — <о)* = 7^-(о) — atco*) (cos — to*) — itQ'e; (4.7)
Здесь обозначено s = k2d%, t = Ti! Te,
1 — (1/0 (vev,-/MeM,-)
L+(VeVi/COeWi) ’
&i = Dt№, Q'e = De [A:f + ky (v|/a)|)].
При выводе (4.7) использовалось условие Яе - Поскольку в плазме
Послесвечения Те да Тi, то для колебаний с ку~^> kz это условие выполни—
■ется при сравнительно небольших значениях магнитного поля. Мы также учли, что в плазме существует стационарное амбиполярное электрическое поле, под действием которого электроны дрейфуют по азимуту (в рассматриваемой нами эквивалентной системе с плоской симметрией по ОУ).
Из (4.7) находим, что плазма неустойчива при
1
“>Т+7 + 'И+*)-^г- (4.8)
Величина а положительна, если и>еы11е1 > Те/Тг. Это необходимое условие неустойчивости по порядку величины согласуется с найденным на эксперименте « 5-ь9 83. Заметим, что при ос > 0 плазма по
Отношению к стенкам заряжена положительно.
Анализ соотношения (4.8) показывает, что колебания раскачиваются лишь при достаточно низкой плотности плазмы, когда выполняется условие (х^,)2 ^ (те1тп1)е11. При этом наиболее неустойчивы колебания с 5 « (хй;)2уз (пг^.'/пг^е)1/3 и кг ^ куе/(ое. В работе 83, однако, отмечено, что значение критической плотности, определенной из эксперимента, примерно на два порядка меньше. Дальнейшее сопоставление теории и эксперимента обнаружило как соответствие по ряду моментов, так и некоторые расхождения. Так, например, в согласии с теорией 83 (см. также (4.7)) частота падала с уменьшением плотности плазмы, а интенсивность шумов возрастала с увеличением магнитного поля, длины разрядной трубки и градиента плотности. В то же время фазовая скорость колебаний на 1 —
2 порядка превышала расчетную. В работе 83 расхождения между теорией и экспериментом были отнесены за счет неточности локального квази - классического приближения. При этом, однако, остается неясным, почему это приближение, с успехом использовавшееся для описания других разновидностей дрейфово-диссипативной неустойчивости, оказывается неудовлетворительным в данном случае.
Проведенное обсуждение показывает, что изучение неустойчивости, наблюдавшейся в плазме послесвечения, не может считаться завершенным. Однако точка зрения, изложенная в 82> 83, уже в настоящее время позволяет понять такие характерные особенности неустойчивости, как низкое значение частоты неустойчивых колебаний (ш < ^г), а также возникновение неустойчивости на поздних стадиях разряда послесвечения, когда плотность плазмы опускается ниже некоторого критического уровня. В то же время не исключено, что физические явления, развивающиеся в плазме послесвечения, имеют более сложный характер. Так, например в 84 на поздних стадиях разряда послесвечения наблюдалась раскачка колебаний даже в отсутствие магнитного поля. Этот результат был интерпретирован как возбуждение звуковых колебаний, в которых участвовала нейтральная компонента плазмы.
5. ИОННО-ЗВУКОВАЯ НЕУСТОЙЧИВОСТЬ
А) Теория
В предыдущих разделах была проанализирована дрейфовая неустойчивость неоднородной плазмы в магнитном поле. Частота дрейфовых колебаний пропорциональна градиенту плотности со « ш* = (сТе1еВ)кук, и поэтому в однородной плазме сама ветвь дрейфовых колебаний пропадает. Однако неоднородность плазмы может приводить к раскачке и таких колебаний, которые характерны для однородной плазмы. Так, например, в неизотермической плазме с Те~^> существует ветвь ионно-звуковых колебаний. (Напомним, что обычно в газовом разряде электронная тем -
|
(ш |-/V,) -/г-г; (1 —) 111 ■<>] * Х(*-‘тёг)"‘=0- м Для упрощения расчетов в (5.1), (5.2) мы перешли в систему координат, где ИОНЫ ПОКОЯТСЯ (0 = 0)' — куУ01, здесь со' —частота колебаний в лабораторной системе координат, „2 |
|
Тшратура значительно превышает ионную Те/Т; « 102. Исключение Магнитного поля, получаем И>п1-- -------- — и3ф1 = 0. (5.1) 1 т; (Й+1У; ^ ' Условие разрешимости системы (1.9), (5.1) приводит к следующему диспер- |
|
— скорость дрейфа ионов в стационарном амбиполярном электрическом поле. В (5.2) также обозначено ДF0 = У0е— - У01 = 70,г?/а>?. Рассмотрим коротковолновые высокочастотные колебания с ку Мах (Л2, vi/cs) при с5 Э - Для определения границы области не Устойчивости, считая 1та) = 0, приравняем нулю по отдельности действительную и мнимую части (5.2). При этом находим со = кус8, V* = с„. При V* > с8 плазма неустойчива. Это условие было получено в работе 41 (см. также 42). Его удобно представить в виде хр(е = т}“1 < 1. На рис. 21 (см. также рис. 3) оно ограничивает область неустойчивости ионно-звуковых колебаппй со стороны больших значений манитного поля. В работе 41, однако, показано, что коротковолновые колебания с кг > е/У Те/те могут быть неустойчивы даже при т] > 1. При анализе таких колебаний поведение электронной компоненты должно описываться кинетически. Область ионно-звуковой неустойчивости ограничена также и со стороны малых магнитных полей. Действительно, во-первых, ларморов - ский радиус электронов должен быть меньше радиуса трубки хреС 1. •Это условие можно представить в виде т] > У те/т1, ему соответствует |
|
|
|
|
|
|
|
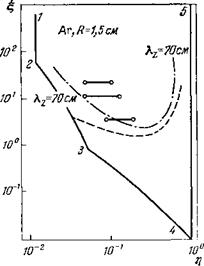
Участок 1—2 границы области неустойчивости. Во-вторых, в 2 отмечено, что при рассмотрении ионно-звуковых колебаний в узких трубках необходимо учитывать эффект выноса плазмы на стенки трубки. При сравнительно низких значениях магнитного поля скорость выноса приближенно равна Dlex, здесь Dle = Dev 1/со|. Если она превысит групповую скорость колебаний, то неустойчивость примет вид сносовой. Это означает, что из-за выноса плазмы в системе не успевают установиться регулярные собственные колебания, и неустойчивость будет наблюдаться в виде хаотического шума. Оценки инкремента показывают, что за время выноса флуктуации не успеют сколько-нибудь значительно возрасти, поэтому плазма будет практически устойчивой. Предполагая, что групповая скорость колебаний равна скорости ионного звука, в качестве условия неустойчивости получаем 2
Cs>DXex. (5.3>
Это условие определяет участок 2—3 границы области ионно-звуковой неустойчивости.
Наконец, стабилизирующее влияние оказывает дрейф электронов в амбипояярном электрическом поле. Расчеты приводят к следующему условию неустойчивости ь)(/vi = £т| > YЬ-,/Ье 41. На рис. 21 соответствующий участок границы отмечен цифрами 3—4.
Мы проанализировали ионно-звуковую неустойчивость слабо ионизованной плазмы. В плазме полностью ионизованной раскачка ионнозвуковых колебаний в столкновительном режиме может осуществляться лишь в весьма ограниченном интервале изменения величины TelTi. Действительно, для того чтобы исключить затухание Ландау на ионах, необходимо потребовать выполнения условия V Te! Ti Э” в то время как из неравенств v„ следует Y(те/тд (Те/Т{)я 1. Интересно
Отметить, что в незамагниченной плазме аналогичные неравенства вообще оказываются противоречивыми 85.
Мы использовали название ионно-звуковые колебания, поскольку при DJt Мах (со, а)*), а) v( закон дисперсии рассматриваемых колебаний имеет вид си2 = к2с (см. (5.2)). В то же время при Dek Min (ш, ш*), ь)^>vt - из (5.2) получаем ш= u>ik2/kyx. Поскольку градиент плотности при этом попадает в знаменатель, то в противоположность дрейфовым эти колебания в ряде работ (см., например, 86) были названы антидрейфовыми.
Б) Эксперимент
Первоначально за ионно-звуковую принимали любую неустойчивость, область раскачки которой на плоскости £ — т} лежала внутри области ионно-звуковой неустойчивости. Так, например, в 41 раскачкой ионно-звуковых колебаний объяснялись аномалии, наблюдавшиеся в высокочастотном разряде в магнитном поле 81. Позднее 45> 78’ 87 была обнаружена и отнесена к ионно-звуковой неустойчивости, граница которой на плоскости £ — т] совпадала с участком 2—3 границы области ионнозвуковой неустойчивости. При более детальном изучении, однако, оказалось, что частота неустойчивых колебаний может быть меньше частоты соударений ионов с нейтралами 12> 46- 88~91. Одного этого обстоятельства достаточно, чтобы считать отождествление неустойчивости с ионно-звуковой несостоятельным. Вместе с тем у нас, например, нет оснований подвергать сомнению выводы работы 92. Здесь изучался разряд постоянного тока в магнитном поле при сравнительно низких давлениях нейтрального газа. Было обнаружено, что при магнитном поле, большем некоторого критического, в разряде возбуждаются шумы и возрастает
|
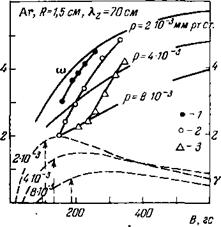
Коэффициент диффузии плазмы. Критическое значение магнитного поля Тические значения безразмерных Однако, как и в случае дрей- = const (ky = mb, ку^>кг). На рис. 23 приведены результаты экспери- В работе50. Из него следует, что, несмотря на большие различия в частоте Те 93, бежали по азимуту в элек- В работах в2'64 проверялось А гораздо более точное дисперсионное соотношение (5.2). На рис. 24 при- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
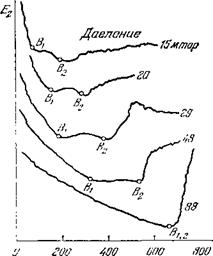
Устойчивой, чем это следует из теории. Действительно, интервал значений магнитного поля, в котором на эксперименте наблюдалась неустойчивость, значительно уже области, где инкремент колебаний, рассчитанный
|
У-10 5, сек |
![]()
|
- I |
![]()
|
Рис. 24. Зависимость частоты ю и инкремента у колебаний с пг = 1 от магнитного поля В 64. |
![]() По (5.2) (штриховые кривые на рис. 24), положителен. Это расхождение можно частично устранить, если учесть, что из-за ухода заряженных частиц на стенки разрядной трубки в действительности могут - наблюдаться лишь колебания, с инкрементом большим обратного времени ухода (ДХех2)-1:
По (5.2) (штриховые кривые на рис. 24), положителен. Это расхождение можно частично устранить, если учесть, что из-за ухода заряженных частиц на стенки разрядной трубки в действительности могут - наблюдаться лишь колебания, с инкрементом большим обратного времени ухода (ДХех2)-1:
1тш > Д1ех2. (5.4)'
|
Давления (мм рт. ст.), температуры (°К): 1 — 2-ю-3, 6 • 10‘; 2—4 • 10-3, 5,2-10‘; 3—8-10"3, 4,2-104. Сплошные кривые — расчетные значения частот, штриховые — расчетные значения инкремента. |
![]() Поскольку обычно Ие со > 1т ш (см. рис. 24), то для крупномасштабных колебаний с ку та к использовавшееся выше условие (5.3) является более слабым, чем (5.4).. Если в качестве условия неустойчивости принять (5.4), то из области неустойчивости на рис. 5.4 исключается интервал магнитных полей, лежащий левее вертикальных пунктирных прямых со стрелками. В результате при малых значениях магнитного поля (левая граница) мы получаем хорошее согласие с теорией, однако на правой границе расхождение остается.
Поскольку обычно Ие со > 1т ш (см. рис. 24), то для крупномасштабных колебаний с ку та к использовавшееся выше условие (5.3) является более слабым, чем (5.4).. Если в качестве условия неустойчивости принять (5.4), то из области неустойчивости на рис. 5.4 исключается интервал магнитных полей, лежащий левее вертикальных пунктирных прямых со стрелками. В результате при малых значениях магнитного поля (левая граница) мы получаем хорошее согласие с теорией, однако на правой границе расхождение остается.
Полезно результаты экспериментов 64 представить на плоскости £ — г) (см. рис. 21). Каждому значению давления (р ~ £-1) на этом рисунке соответствует отрезок горизонтальной прямой, длина и положение которого определяется интервалом изменения магнитного поля (т] ~ В). Мы нанесли лишь ту часть отрезка, которая соответствует неустойчивости плазмы. В результате получаем три отрезка, параллельных оси т]. На этом же рис. 21 штриховой линией показана область неустойчивости первой моды колебаний, найденная из решения (5.2), и штрих-пунктиром — полученная с учетом условия (5.4). При расчетах в соответствии с экспериментом продольная длина волны принималась равной удвоенной длине плазмы. Если увеличивать продольную длину волны, то область неустойчивости расширяется. Заметим, что полная область ионно-звуковой неустойчивости, ограниченная на рис. 21 сплошной линией, получается в результате наложения областей неустойчивости отдельных мод в системе, неограниченной вдоль магнитного поля (оо^кг^ 0), при ку ^ х.
Зависимость частоты ионно-звуковых колебаний от магнитного поля изучалась также в разряде постоянного тока в продольном магнитном поле 58. Были получены примерно те же результаты, что и в плазме высокочастотного разряда.
Исследование зависимости частоты неустойчивых колебаний от давления нейтрального газа и волнового вектора было проведено в работе 64. На рис. 25 приведены опытные и расчетные зависимости частоты колебаний со от давления газа р, полученные в 64, в аргоновой плазме. Здесь так же, как и на последующих рисунках, штриховой линией обозначена граница неустойчивости, рассчитанная из дисперсионного уравнения (5.2),. а штрих-пунктиром — граница, найденная из условия (5.4). Из рисунка.
Видно, что при всех давлениях выполняются условия 0) > vг, 0)г. Прет уменьшении продольной длины волны и давления газа в соответствии с теорией наблюдается увеличение частоты колебаний. Заметим, что. н условиях 64 продольная длина волны уменьшалась ~
|
✓Л2= ВО см, Ку=70см =80 см |
|
1,5 см} 8=200гс |
![]()
|
Р, ммрг. сТ. |
![]()
|
Рис. 25. Зависимость частоты неустойчивых коле-» баний ш с т = 1 от давления газа р 64. Продольные длины волн (см): 90 (I), 80 (2), 70 (3) и 60 (4)^ Штриховой линией дана граница области неустойчивостик рассчитанная по (5.2), штрих-пунктирной — граница», найденная из условия (5.4). Сплошные кривые для = =60—90 см — расчетные значения частот. |
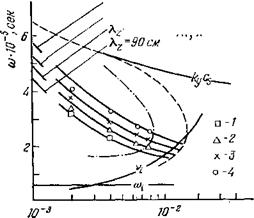 ОТ щах = 90 СМ ДО кг =
ОТ щах = 90 СМ ДО кг =
= 60 см, определяемой возможностями использованной экспериментальной установки. При этом частота колебаний с к2 = 60 см при низком давлении газа была близка по величине к кус3. В 64 изучалась также зависимость частоты колебаний со от волнового вектора к. Частота колебаний со в функции от кг (к2 — проекция волнового вектора на направление магнитного поля) представлена на рис. 26.
Из рисунков видно, что, как и следует из (5.2), частота увеличивается с ростом магнитного поля В и с уменьшением давления газа р. Она оказывается меньше кус3, приближаясь к этому значению с уменьшением продольной длины волны Яг = (кг = 2 я/к2)^
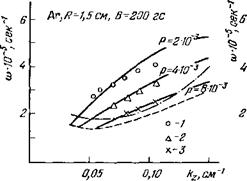
|
А) |
![]()
|
Рис. 26. Зависимость частоты неустойчивых колебаний и с я = 1 от проекции вол~ Нового вектора на направление магнитного поля 84. В) Давления (діж. рт. ст.): 2-10-* (1), 4-Ю-3 (2) и 8-Ю-3 (3); б) магнитные поля (гс); 200 (I) и 300 (2). Обозначения те же, что и на рис. 25. |
![]()
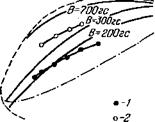
|
0,05 0,10 к2, см Т Б) |
![]() Аг, й=1,5см, р-2-10~3ммрт. ст.
Аг, й=1,5см, р-2-10~3ммрт. ст.
Как видно из рис. 26, а, максимальное давление, выше которого плазма становится устойчивой, было близко к 8*10_3 мм рт. ст. и сравни^ мо с полученным из расчетов (штриховая и штрих-пунктирная линии). Заметим, что со стороны низких давлений теория не дает ограничения на неустойчивость. Экспериментально в 84 давление газа уменьшалось
До значений ^ 10-3 мм рт. ст. и при этих давлениях в плазме все еще обнаруживались неустойчивые колебания. Из уравнения (5.2) нельзя получить ограничения на область неустойчивости со стороны малых
|
|
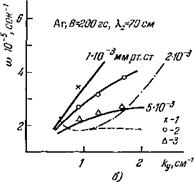 Тис. 27. Зависимость частоты неустойчивых колебаний ш от проекции волнового вектора на азимутальное направление ку м. о) Магнитные поля (гс); 120 (I), 200 (2) и 300 (3); б) давления (мм. рт. ст.): 1-10-*О), 2-10-д (2) и 5-10_3 (3) Обозначения те же, что и на рис. 25.
Тис. 27. Зависимость частоты неустойчивых колебаний ш от проекции волнового вектора на азимутальное направление ку м. о) Магнитные поля (гс); 120 (I), 200 (2) и 300 (3); б) давления (мм. рт. ст.): 1-10-*О), 2-10-д (2) и 5-10_3 (3) Обозначения те же, что и на рис. 25.
Магнитных полей (штриховая кривая на рис. 26, б открыта снизу). Такое ограничение дает условие (5.4) — штрих-пунктирная кривая.
На рис. 27 приведена зависимость ш от ку. Из него так же, как и из рис. 26, видно, что экспериментальные данные, представленные на нем, Достаточно хорошо согласуются с расчетными.
ЗАКЛЮЧЕНИЕ
Таким образом, к настоящему времени установлены условия, при которых должна развиваться дрейфово-диссипативная неустойчивость, и проанализированы дисперсионные свойства неустойчивых колебаний малой амплитуды. В этих вопросах теория и эксперимент согласуются между собой вполне удовлетворительно. Можно надеяться, что некоторые численные расхождения будут устранены при более полном учете эффектов, связанных с неоднородностью плазмы и нелинейностью колебаний. Возможно, что для этого потребуется также переход от гидродинамического описания к кинетическому.
Наряду с этим следует помнить, что к настоящему моменту не установлена физическая природа ряда колебаний, развивающихся в плазме газового разряда в магнитном поле. Не исключено, что при их исследовании будут выявлены новые аспекты влияния неоднородности замагни - ченной плазмы на ее колебания, не включенные в механизм дрейфоводиссипативной неустойчивости.
Авторы благодарны Б. Б. Кадомцеву за просмотр рукописи и ценные замечания и А. А. Рухадзе за полезное обсуждение.
Институт Атомной энергии им. И. В. Курчатова Московский государственный университет им. М. В. Ломоносова