Численное решение уравнения Фоккера—Планка
П /1
При численном решении стационарного уравнения (1), где —^ определяется системой (20)—(21), удобно путем параметризации включить его в указанную систему.
|
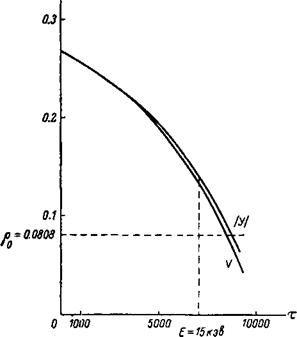
Ряс. 3. Характеристика замедления частицы. У — положение однородного в«втр*: V — бвар*ам«рвая окорость аона. |
В самом деле, в стационарном случае п определяется решением следующей задачи Коши
Лп Г /сч М а Г</тг2“П
|
(2 |
![]() Ж = - Г(£)-4-Т5£Ы[л’
Ж = - Г(£)-4-Т5£Ы[л’
= п0 при Е > £0
О 12 Журнал технической фпжикн, № 11, 1965 г.
Где Е принимает значения: 62.5 кэв = Е0^ Е^ Е* —15 кэв, т. е.
Мю*
В том же интервале, что и величина, равная энергии отдельного
Иона; при этом величина Е=Е0 достигается отдельным ионом лишь при £ = 0.
Полагая Е=-у, где V, определяемая системой (20)—(21), а тем
Самым Еу является функцией параметра t, переходим к следующим безразмерным величинам: л=гл0л*; £* = и)/; v = v0V (и>, v0— прежние значения).
Тогда
|
V (Е) = и»* (V), >* (V) = 0.81/ - 10“*-19-5У (27) |
|
Г |
|
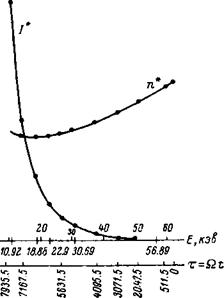
Рис. 4. Распределение относительной плотности быстрых ионов и потока нейтральных частиц в исследуемом интервале анергий. |
|
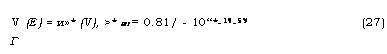 |
 |
Энергия, выраженная в килоэлектронвольтах, оказывается равной
Е=868.4У2 (28)
И задача, подлежащая численному интегрированию, принимает вид
^т = — У*о<У) агс 5'п VI— о2,
(29)
|
</2 (К2) |
|
С1п* ИГ |
![]()
|
ЫП1 |
![]() (30)
(30)
|
С1{У2) (1Г |
(31)
К (0) = 0.268; К(0) =—0.268; л*(0) = 1. Величина о имеет прежнее значение, а производные от (V2), входящие в уравнения (31), выражаются аналитически из уравнений (29), (30).
Решая задачу (29)—(31), мы определяем: а) процесс замедления
Отдельного иона [соответственно получаем оценку „времени жизни“
Отдельной частицы (29)—(30)]; б) зависимость п(Е) в стационарном случае [уравнение (31) совместно с выражением (28)]; с) кроме того, параллельно вычисляется поток нейтральных частиц. Величина последнего в безразмерных величинах дается формулой
/‘(£) = Ш) = °.9V'l• 10"OM5'/J/i*(Ј) = 26.5V • 10'1,sv"*- (32)
Задача (29)—(31) решалась на быстродействующей вычислительной машине с помощью метода Рунге—Кутта, с абсолютной точностью на шаге в — 10“*.
На рис. 3 представлены характеристики замедления отдельной частицы, полученные из системы (29)—(31) (для удобства сравнения представлен график | У (t*) |), отсюда следует, что граничное значение энергии £=15 кэв (V ^0.13) достигает при t* • 103, т. е. за теоретической границей применимости осредненных уравнений. Однако численное интегрирование точных уравнений (14')—(15^) на интервале показывает, что здесь осредненные решения совпадают с точными по - крайней мере до двух верных знаков. Это обстоятельство позволяет предполагать, что на интересующем нас интервале осреднение дает удовлетворительное совпадение с точным результатом. Распространяя результаты осреднения на весь участок интегрирования, можем сделать вывод, что время жизни отдельной частицы Af* Ю4; / 3 • 10“4 сек*
На рис. 4 представлена зависимость п* = п*(£) и Г (Е) соответственно в допустимом постановкой задачи интервале энергий: 62.5 кэв ^ ^ Е^ 15 кэв.
Оказывается, что плотность частиц на указанном интервале энергии убывает в стационарном процессе на 35%. На рис. 4 наряду с энергетической нанесена и временная шкала, что позволяет проследить за л(£, t) и /(£, /) в нестационарном режиме после выключения тока инжекции.
В заключение выражаем глубокую благодарность Л. И. Артемен- кову за большой интерес и полезные обсуждения как При постановке задачи, так и при анализе результатов.
Лштератур«
[1] Б. А. Трубников. Вопросы теории плазмы, вып. 1. Госатомиздат, М.». 1963. — [2] С. F. Barnett, W. В. Gauster, J. A. Roy. ORNL-3113, стр. 34, 1961. — [3] H. Н. Боголюбов, Ю. А. Митропольский. Асимптотические методы в теории нелинейных колебаний. Гостехиэдат, 1955. — [4] В. М. Волосов. ЖВМ, вып. 1, 1963. — [5] Т. К. Fouler, М. Rankin. J. Nucl. Energy, ч. с., 4> 311, 1962.
Московский Поступило в Редакцию
Государственный университет 12 марта 1965 г.
Им. М. В. Ломоносова Физический факультет
1966 ЖУРНАЛ ТЕХНИЧЕСКОЙ ФИЗИКИ Том XXXVI, в. 10
1966 JOURNAL OF TECHNICAL PHYSICS Vol. XXXVI, № W