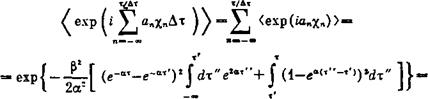ФИЗИКА ПЛАЗМЫ

АНОМАЛЬНАЯ ДИФФУЗИЯ РАЗРЕЖЕННОЙ ПЛАЗМЫ В АДИАБАТИЧЕСКИХ ЛОЙУШКАХ

С. В. Путвинский, А. В. Тимофеев

Показано, что если в плазме возбуждены же лобковые колебания, то даже редкие кулоновские соударения могут вызывать заметную диффузию плазмы. Обсуждаемый механизм диффузии по своему характеру близок к* механизму неоклассической диф­фузии. В обоих случаях перенос частиц поперек магнитного поля происходит по детерминированным траекториям, а кулоновские соударения лишь перебрасывают заряженные частицы с одной траектории на другую.

Введение

Адиабатические ловушки часто работают в режиме постоянной и дли­тельной (порядка нескольких секунд) инжекции плазмы. В таком режиме стационарный уровень плотности плазмы устанавливается в результате баланса между поступлением частиц в ловушку за счет инжекции и ухо­дом из-за перезарядки на остаточном газе. Если плотность плазмы пре­вышает некоторое критическое значение, то в ловушках с простым про­бочным полем возбуждается так называемая желобковая неустойчивость. Довольно часто развитие этой неустойчивости приводит к установлению нового стационарного состояния [*]• При этом в плазме присутствуют регулярные колебания постоянной амплитуды, а сама плазма довольно быстро уходит на стенки камеры. Какие процессы приводят к выбросу плазмы, до сих пор оставалось непонятным. Действительно, регулярные периодические колебания не могут вызывать направленного движения частиц, а типичные для обсуждаемых экспериментов значения плотности плазмы настолько низки, что диффузионный поток, рассчитываемый по классической теории, должен быть совершенно ничтожным.

В настоящей работе показано, каким образом при низкой плотности плазмы упорядоченные колебания могут приводить к потере частиц из адиабатических ловушек. В предлагаемом механизме потерь существенно учитываются некоторые особенности адиабатических ловушек. В них ионы удерживаются магнитными пробками, а электроны — электрическим потенциалом, который возникает самопроизвольно. Наибольшего значения потенциал достигает в центре ловушки, и он спадает как вдоль магнит­ного поля, так и в поперечном направлении. Поскольку стенки камеры поддерживаются при постоянном потенциале, равном нулю, то радиаль­ное электрическое поле должно зависеть от координаты вдоль магнитного поля (координата г). Частота колебаний электрона в потенциальной яме вдоль магнитного поля значительно превосходит частоту желобковых ко­лебаний. Поэтому при рассмотрении последних следует использовать ус­редненное по 02, значение радиального электрического поля. Результат усреднения зависит от того, насколько далеко в пробки заходит электрон, т. е. в конечном счете от энергии его продольного движения.

Радиальное электрическое поле приводит к дрейфу электронов по азимуту. В этом же направлении бегут и желобковые колебания. В же -

Лобковых колсбанпях электроны колеблются поперек магнитного поля, причем амплитуда смещения зависит от рассогласования между фазовой скоростью желобковых колебаний и скоростью дрейфа электрона. Ввиду того что скорость дрейфа в свою очередь зависит от энергии, кулоновские соударения должны приводить к хаотическим изменениям амплитуды смещений электрона в желобковых колебаниях. Этот процесс, как показа­но в настоящей работе, вызывает аломально быструю диффузию электро­нов поперек магнитного поля. Ее механизм имеет много общего с механиз­мом неоклассической диффузии (см., например, [г]).

В настоящей работе рассматривается диффузия электронов, однако аналогичным образом могут диффундировать и ионы. Действительно, амплитуда колебаний иона вдоль магнитного поля, а следовательно, и среднее радиальное электрическое поле, действующее на ион, зависят от соотношения между энергиями движения иона в направлении вдоль п поперек магнитного поля. Помимо того в адиабатических ловушках к дрейфу ионов в скрещенных йолях добавляется дрейф из-за неоднородно­сти магнитного поля, скорость которого пропорциональна энергии иона. Частота ион-ионных кулоновских соударений в адиабатических ловушках обычно очень низка, однако энергия ионов может меняться, например, под действием циклотронных колебаний, которые очень часто самопро­извольно возбуждаются в таких системах.

1. Основные уравнения

Адиабатические ловушки с простым пробочным полем представляют собощ аксиально-симметричные системы. Для упрощения расчетов заме­ним аксиальную симметрию плоской. Введем декартову систему коорди­нат, направив ось ОЪ вдоль магнитного поля. Поставим ось ОУ в соот­ветствие азимуту, а ось ОХ — радиусу. Рассмотрим движение электрона в электрическом поле с потенциалом

Ф(г, *)=фо(*, 2)+ф4(у, г).

Здесь фо{х, г)=ф0(х) (1— (г/Ь)г) моделирует постоянный потенциал, удер­живающий электроны в ловушке, а ф4 (у, (ку—Ш) — потенциал

Желобковых колебании. Уравнения движения электрона имеют вид

И

С с£ф0

У “11 Их

(3)

771 ъ

Поскольку частота желобковых колебаний мала по сравнению с электрон - но-циклотронной, а длина волны велика по сравнению с электронным лар- моровским радиусом, то для скорости движения электронов поперек маг­нитного поля мы приняли выражение УявсЯ’"*[НУф].

Учитывая (3), усредним уравнение (2) по быстрым колебаниям вдоль магнитного поля:

У Ы Ох 2еФ. ]

Здесь е,| — энергия движения электрона в направлении вдоль магнит­ного поля, взятая в точке г—Ю, т. е. на дне потенциальной ямы.

Для дальнейшего весьма существенно, что среднее электрическое поле, а вместе с ним и средняя скорость дрейфа зависят от продольной энергии электронов. Очевидно, что такая зависимость будет возникать при любом виде потенциальной ямы, кроме прямоугольной. Поскольку точный вид потенциала фо(г), возникающего в ловушке, неизвестен, мы приняли простейшую параболическую зависимость.

Под действием кулоновских соударений энергия электрона флуктуи­рует около некоторого среднего значения ец0. Простейшее модельное урав­нение, описывающее эти флуктуации, имеет вид

6е„=-^бе„-£ (*). (5)

Здесь беи=ец—ец0 — частота кулоновских соударений, £ (£) — случайная функция, б-коррелированная во времени:

(£*) )=ст2б(£1—о~=2Тцгу, Г|,«ец0.

Скобки означают усреднение по статистическому ансамблю.

Из (5) следует 0

Г

88,- (6)

— оо

Используя (6), приводим (4) к виду

— 09

Для дальнейших вычислений удобно ввести следующие безразмерные переменные:

Х=п+ку—©£, =х<пН/ксу^ т=Ш.

Тогда уравнения (1), (7) будут иметь следующий вид:

TOC o "1-5" h z вт т|, (8)

Й\

Здесь

V ки / Тп с

«=-, ш (Г,„ (I) = (!-_-) -1, V--—,

Ки 1

Ю* 2еф0 ’

<Х (т.) X Ы >=Р26 (т,—т2),

___ 1 (киУ( °° У.

© © / 2е<ро *

° Замена нижнего предела интегрирования на —°° законна при рассмотрели медленных процессов с характерным временным масштабом *0^”* (ат0>1).

2. Однородное электрическое поле Л. Механизм диффузии

Если стационарное электрическое поле однородно и, следовательно, скорость дрейфа по 0¥ не зависит от £(и>(£, е)=и;(е), ) = ш), то

Уравнения (8), (9) могут быть проинтегрированы:

Х

TOC o "1-5" h z 6(т)-6(0)- рт'зт^т), (10)

О

X х'

Л(т)=п(0)+шт - |«гт' | йт"е-('"-,'’х(т"). (И)

О —а»

Предположим, что мы выключили кулонавскые соударения (х^О), тогда траектории электронов на плоскости Л примут вид синусоид (см. рис. 1). При это-м чем меньше разность между фазовой скоростью

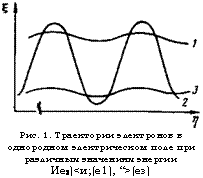Колебаний и скоростью дрейфа электро­на, т. е. чем меньше м>(е), тем больше амплитуда синусоиды. Пусть сначала величина ш (е) велика — электрон на­ходится на траектории, обозначенной цифрой 1. Под действием кулонов ежих соударений его энергия может изменить­ся таким образом, что величина ш(е) уменьшится, тогда электрон перейдет на траекторию 2. Если в тот момент« когда электрон находится в нижней ча­сти траектории 2, его энергия опять воз­растет, то он перейдет на траекторию 3. Конечным результатом этих процессов является смещение электрона по оси 6, т. е. поперек магнитного поля. Нетрудно заметить, что рассматриваемый нами механизм диффузии близок по своему характеру к механизму нео­классической диффузии, например, [2]. Действительно, в обоих случаях частица смещается поперек магнитного поля по детерминированным траекториям, а 1кулоновские соударения лишь перебрасывают частицы с одной траектории на другую.

Б. Коэффициент диффузии

Найдем с помощью (10), (11) дисперсию в значениях координаты г:

£г,(т)=<я2>-(<Я>)2=-^-г(е"'“-1+а1), (12)

2а‘

А также скорость, с которой изменяется дисперсия в значениях координа­ты

Я;М = -~-с^(т)=2 ^ зтт|(т) | <2т' зт г (т') ^ —

Из (12) следует, что возрастает со временем. Будем рассматривать

Интервалы времени т, удовлетворяющие условию т»т!*, где Т1* определя­ется равенством <2т,(т1*)вя. В этом случае в (13) можно опустить второе слагаемое. Ниже мы увидим, что для достаточно больших интервалов вре­мени величина /)*(т) стремится к конечному пределу Вг(т) при т-*°о. Этот предел имеет смысл коэффициента диффузии:

(14)

Интеграл в (14) представляет собой некоторую разновидность инте­грала по случайным траекториям, введенного Винером. Для его вычисле­ния воспользуемся стандартной методикой (см., например, [а]). Заменим в (11), (14) интегралы суммами. В частности, представим разность Л СО—“П СО в виде

(15)

Где

Ап=а~1 (е~ах—е~ах') при п<т'/Дт, ая=а-1(е-в(’-яАт,-1) при л>т7Дт.

Примем, что величина %п=%(п&'%) распределена по нормальному за-

Кону:

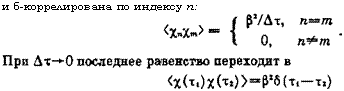(16)

(17)

(ср. с (5)). Производя в (14) усреднение с помощью (16), (17) и возвра­щаясь от суммирования к интегрированию, получаем

(18)

В результате выражение для коэффициента диффузии Л* принимает сле­дующий вид:

О

Нам удалось взять интеграл (19) лишь в простейших предельных слу­чаях. Предположим, что выполняется условие р>тах(27,а % 2аш'/*), тогда в (19) можно положить соз(м>т)=1, а показатель экспоненты разложить в ряд до второго порядка включительно:

(ла)7*

2^

При 2а'/,ш>р>2'/,а,/1 подынтегральное выражение в (19) быстро осцилли­рует и. для вычисления интеграла следует воспользоваться асимптотиче­скими методами (см., например, [4]):

/)62«Р2/4ш (21)

Наконец, при р<2'/,а,/1 в показателе экспоненты в подынтегральном выра­жении можно оставить лишь первое слагаемое

(>г

4сс2(ш2+р‘/4а‘)

Зависимость коэффициента диффузии от частоты соударений схемати­чески изображена на рис. 2 (ср. с аналогичной зависимостью коэффици­ента неоклассической диффузии [*]). Здесь следует напомнить, что при

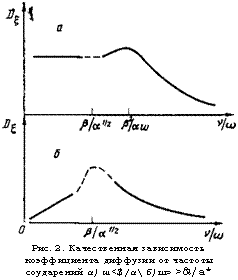Вычислении коэффициента диффузии мы использовали условие т»а~* (см. выше), поэтому полученные на­ми выражения пригодны лишь для описания медленных процессов с ха­рактерным временным масштабом £0, много большим V“1.

В. Уравнение диффузии

Как известно (см., например, [5])т случайные процессы, длительность которых значительно превышает вре­мя «расцепления корреляции» т*, мо­гут быть описаны диффузионным уравнением типа уравнения Фокке - ра —Планка. Мы примем т*= =тах(т<"), где 1=1, 2, 3. Время т»* было определено выше (см. предыду­щий раздел) как время размешива­ния по координате т (^п(т1в)=я).

При т>т!* в уравнении Фоккера — Планка можно не учитывать зависимость от этой координаты. Помимо того при т>т!* обращается в нуль коэффициент динамического трения Л(т) =<£>=<зт т]> (см. (8)). В результате уравнение диффузии прини­мает следующий вид:

Здесь /=/(!, т) — функция распределения электронов, <?(5, т) — функция источников.

Время т2* собственно и имеет смысл времени расцепления корреляций в значениях координаты 5: А(т) =^£=сопз1; здесь /)6(т) определено вы­ражением (13). Наконец, время т3* равно а“1. При т»т3* электрон «за­бывает» о начальном значении энергии, и поэтому при рассмотрении про­цесса диффузии можно использовать функцию распределения, не завися­щую от энергии электронов. Это приближение представляется разумным, поскольку обычно время удержания электронов в адиабатических ловуш­ках значительно превышает время между соударениями V1.

Рассмотрение показывает, что выражение для т* можно привести к следующему виду:

Т*=тах(сг1, а2/{*2). (24)

Определим также характерный пространственный масштаб, на кото­ром происходит расцепление корреляций Величина V эквивалентна длине свободного пробега в обычной гидродинамике. При достаточно ма­лых значениях ш она равна пробегу электрона за время т* между соуда­

Рениями 5'=т‘» ПРП больших — амплитуде смещения электрона в поле желобковых колебаний. Используя эти соображения, находим

?*=сг р>тах(2,/1а 2аш7’),

Г=а2/р2, 2,/‘а^»р>2,/1аш' (25)

27,а шг/,»р.

В заключение заметим, что в выражение для размерного коэффици­ента диффузии Бх=0^х/ д)г6,х/йЬ частота колебаний со входит лишь че­рез разность ы—ки. Этот коэффициент диффузии отличен от нуля при

О)=0, и, - следовательно, к диффузии электронов могут приводить даже статические возмущения электрического потенциала.

[1] Неоднородное электрическое поле

А. Движение в отсутствие соударений

Неоднородность стационарного электрического поля особенно сильно влияет на движение электронов, если где-то в пределах системы фазовая скорость колебаний совпадает со скоростью дрейфа, т. е. величина ш(£) обращается в нуль. Рассмотрим движение в окрестности резонансной точ­ки. Разложим в этой области ш(£) в ряд и оставим лишь первый член разложения ш(£)«а£; здесь а=йш/Л%\ят0, начало координат помещено в резонансную точку. Если кулоновские соударения отсутствуют, то систе­ма уравнений (8), (9) принимает стандартный вид:

Д/(1'1=— зт Т|, <й|/с£т=а£. (26)

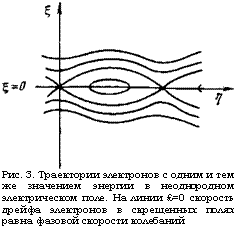
Именно такие уравнения описывают, например, движение заряженных частиц в задаче о нелинейном затухании Ландау [•]. Эта задача к на­стоящему времени детально изучена, и поэтому полезно сопоставить ее с рассматриваемой нами. В задаче о нелинейном затухании Ландау ока­залось удобным разделить все частицы на захваченные волной и пролет­ные. На плоскости 5л захваченные частицы располагаются в окрестности линии 6*=0. Поскольку для таких частиц приближенно выполняется усло­вие резонанса, то опи подвержены особенно сильному воздействию со стороны колебаний. В нашем случае явление захвата состоит в том, что желобковые колебапия заставляют частицы двигаться по О У со средней скоростью, равной фазовой скорости колебаний. На рис. 3 траектории захваченных частиц изображены замкнутыми линиями. Область захвата

Ограничена значениями |£|<а-,/,_ Пролетные частицы движутся отно­сительно волны, на рис. 3 им соот­ветствуют незамкнутые траектории. Б. Коэффициент диффузии Кулоновские соударения вызы­вают хаотические изменения энергии электронов. Вместе с энергией флук - туирует положение резонансной точ­ки, которая выбрана нами в качестве начала координат, а следовательно,, дрожит, как единое целое, и вся изо­браженная на рис. 3 картина фазо­вых траекторий. Такое дрожание

Ограничивает фазовую память элек­трона и приводит к тому, что элек­трон в конце концов сбивается

С траектории. Если характерное вре­мя расцепления фазовых корреляций т* много меньше периода обращения по траектории 2я/й, то электрон не успевает «почувствовать» неоднород­ности системы. В этом случае мы можем использовать результаты, полу­ченные во втором разделе, учитывая зависимость ш от | параметрически. Такой режим движения мы будем называть режимом частых соударений. Следует, однако, отметить, что частота меняется при переходе с одной траектории на другую. По этой причине соударения, частые в какой-то

Области на фазовой плоскости, могут оказаться редкими в других об­

Ластях.

Если выполняется условие йт*>1 (режим редких соударений), то фа­зовая память электрона охватывает много периодов колебаний. В этом случае можно считать, что электрон движется по орбитам, изображенным на рис. 3, медленно переходя с одной орбиты на другую. В режиме редких соударений их влияние на движение электрона можно учесть в рамках метода последовательных приближений, что и будет сделано ниже.

При ш(£)=а£ уравнения (8), (9) могут быть получены из гамильто­ниана

1 *

TOC o "1-5" h z Н = — аг-соз л-5 (т') еа{х'~х). (27)

Движение, не возмущаемое кулоновскими соударениями (см. (26)), удоб­но описывать переменными действия:

7'“’ - ^ Е (т-) -со"'- <28)

0(о)=от+СОП81. (29)

Здесь

/ 1 / 1+Н ч*

0(/)-лЛ«*К-‘*-(■—) . (30)

Но — невозмущенный гамильтониан, К и Е — полные эллиптические интег­ралы первого и второго рода соответственно.

Уравнения (28), (29) описывают траектории пролетных частиц. Для захваченных частиц можно было бы привести аналогичный выражения. Однако, как мы увидим в дальнейшем, захваченные частицы играют весь­ма малую роль в интересующих нас процессах.

Кулоновские соударения изменяют действие и фазу в соответствии с уравнениями

(31)

А о д£(0)

(32)

(33)

{пАлу 4а а*+(га£2)1 '

П— 1

Здесь скобки со значком 6 означают усреднение по начальной фазе.

Вдали от резонансной области (5»1/о'л) /-*£ и соответственно £)/ переходит в В этом легко убедиться, если учесть, что Лn~(a£2)■',^+,/, и поэтому при |>1/а,/а в (34) можно оставить лишь первый член ряда

4шг(!) а2+ш*(£) ’

Здесь использованы равенства й«2/са'л«а£«ш(|).

В зависимости от соотношения между а и ш(|) (35) переходит в (21) или (22). Последнее имеет место лишь, если Это ограничение

Вполне естественно, так как метод последовательных приближений, использованный в настоящем разделе, справедлив при достаточно малых значениях р.

Выражение (35) является первым членом разложения по квадрату отношения амплитуды смещения электрона в поле желобковых колебаний б£~1/а£ к расстоянию до резонансной точки 5- При б£<5 неоднородность системы можно считать слабой и вполне естественно, что в этом случае можно использовать выражения, полученные в разделе 2Б, учитывая зависимость электрического поля от координаты параметрически.

В настоящем рассмотрении предполагалось, что кулоновские соударе­ния оказывают малое воздействие на движение электронов. Это предполо­жение нарушается в окрестности сепаратрисы, разделяющей пролетные и захваченные частицы, где й(/)-*-0. Однако в дальнейшем мы покажем (см. раздел ЗГ), что эта область дает малые вклады в величины, имеющие реальное значение для эксперимента.

В. Коэффициент динамического трения.

Уравнение диффузии

В уравнение Фоккера — Планка наряду с коэффициентом диффузии входит коэффициент динамического трения. Выше мы показали, что если электрическое поле однородно, то коэффициент дипамического трения обращается в нуль. Найдем его для случая, когда неоднородность электри­ческого поля может учитываться параметрически, т. е. для режима частых соударений, а также для режима редких соударений вдали от резонансной области.

В нулевом приближении по неоднородности Јo=const, а г|0 (т) дается (11). Следующее приближение определяется уравнениями

TOC o "1-5" h z = sin Ло(т), (36)

Ri=ali. (37)

Из второго приближения нам понадобится лишь уравнение

|г=—ть(т) cos Ло(т). (38)

Усредняя (38) по статистическому ансамблю, получаем

Х

Л«<£2>=--^-| ат,(т,-т)<зт(т1о(т')-т1о('г))>. (39)

— ав

С другой стороны, выражение для коэффициента диффузии можно пред­ставить в виде

1 Г

А=<11|1>=у] (гт'<соз(я.(т')-т1о(т))>. (40)

Поскольку рассматриваются большие интервалы времени т>т*, нижний предел интегрирования в (39), (40) взят бесконечным.

Из (39), (40) следует, что коэффициент диффузии и коэффициент динамического трения удовлетворяют соотношению Р%=(Ю1/(1, а следова­тельно, уравнение Фоккера — Планка принимает вид (ср. с (23))

Я/ д - */

У - Д,^г=<?(и). (41)

Д1 дъ д

В режиме редких соударений в окрестности резонансной точки удобно использовать переменные действия. Простые, но значительно более длин­ные выкладки приводят к соотношению FI=dD^ldI, а следовательно, и в переменных действия уравнение диффузии принимает вид, аналогич­ный (41). Использование уравнения диффузии, содержащего единствен­ную переменную /, возможно, если по фазе происходит быстрое усредне­ние. Можно показать, что в выражении для дисперсии по 0 содержится слагаемое (Q't)гdI, где <2, —дисперсия по /. Таким образом, в интересую­щем нас режиме редких соударений От*>1 функция распределения долж­на действительно очень быстро размазываться по углу 0.

Г. Усредненный коэффициент диффузии

Экспериментальные данные обычно содержат сведения о некотором усредненном коэффициенте диффузии. Вычислим его для следующей модельной задачи. Рассмотрим слой плазмы Будем считать, что
через левую границу £=?1, которая соответствует центру аксиально-сим­метричных систем, поток частиц отсутствует и что все частицы погло­щаются на правой границе £=£2 (стенке). Рассмотрим стационарный про­цесс дf/дt=0 при ^ =сопз1. Вве­дем средний коэффициент диффузии Бг, определив его таким образом, чтобы в эквивалентной однородной системе того же размера Д£=£2— при том же значении функции источ­ников ($ получить правильную вели­чину перепада функции распределе­ния А/=/(^2) —/(€1) - Несложные вы­числения дают

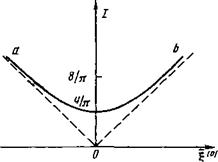(42) рис. 4. Зависимость действия I от сред -

Иа выражения (42) следует, что, чем него на траектории значения коорди - т~ / с «гг наты с( Захваченным частицам соот -

Меныпе значение -^М£) в данной об - ветствует ОТрезок оси ординат (0,8/я),

Ласти, тем больший вклад дает эта пролетным — кривая аЪ

Область в Т). Этот результат вполне естествен, так как области с наи­меньшим значением оказывают наибольшее сопротивление потоку — в них частицы задерживаются наибольшее время.

Если в интервал (£ь £2) попадает резонансная точка, то выражение

(42) справедливо лишь для режима частых соударений. Режим редких соударений требует специального исследования. Предположим, что зона, занятая захваченными частицами, составляет малую часть системы %^>а~'1г и расположена внутри ее. В этом случае траектории электронов у границы (5=51.2) близки к прямым линиям. Мы надеемся, что резуль­таты, полученные при исследовании этой задачи, по крайней мере качест­венно описывают большую часть возможных экспериментальных ситуа­ций. Действительно, если плазма ограничена металлической стенкой, то как бы ни была велика резонансная зона и где бы ни была она расположена все-таки у края плазмы электрический потенциал обращается в нуль, а следовательно, траектории электронов близки к прямым линиям. В этой области смещения электронов поперек магнитного поля минимальны, и поэтому именно она определяет величину среднего коэффициента диф­фузии.

Для дальнейшего существенны два обстоятельства: во-первых, у грани­цы плазмы (|£|^>Д~/’) имеет место приближенное равенство %~1, а сле­довательно, /Ш~/(0> во-вторых, в силу того, что преобразование г]-►/, 0 является каноническим, (?(£, т])=(?(Л в)*

Для вычисления среднего коэффициента диффузии, как и в режиме частых соударений (см. выше), найдем разность Д/=/(Ы“/(£О - В ста­ционарном случае она определяется пролетными частицами, в то время как в области захвата /^сопэЬ. Поясним это положение рис. 4. На нем изображено действие I в функции от среднего на траектории значения £(0)=£2 (см. (33)). Для захваченных частиц |(0)=0 и поэтому они распо­лагаются на оси ординат 0</<8/я. Из рис. 4 следует, что частица может перейти из области |(0><0 в область |(в)>0, минуя область захвата. Если же она за хватится волной, то одновременно с этим другая частица должна перейти из захваченных в пролетные. По этой причине полный поток через область захвата равен нулю, а /(/) в этой области постоянна. Вклад
пролетных частиц в Д/ находим из уравнения, диффузии, аналогично­го (41):

*!• Ы1

А/--- 2 <? | ——. (43)

8/я 1

Здесь для простоты рассматривается симметричная система £1=—£2. В то же время в однородном случае мы, очевидно, имели бы Д/—2@£2*/15. Со­поставляя это выражение с (42), получаем

/г 1М -1

В-*' I— • <42 )

4/Я

Это выражение аналогично (42). Различие в численном коэффициенте обязапо тому обстоятельству, что в силу симметрии системы интегрирова­ние идет лишь по области £>0.

Коэффициент диффузии довольно резко спадает с удалением от области, занятой захваченными частицами (см. (35)). Поэтому интеграл

(43) , как и (42'), определяется областью у границы плазмы

Ш2(Ь) а!+7,ш! Ш

Заключение

Таким образом, мы показали, что при наличии желобковых колебаний кулоновские соударения могут приводить к аномально быстрой диффузии плазмы. Получены выражения для коэффициента диффузии (см. (19) — (22), (35), (42), (44)), которые могут быть использованы при сопостав­лении с экспериментальными данными.

В частности, оценка коэффициента диффузии с помощью (21), кото­рую следует использовать в условиях эксперимента [1], дает /)=Д«д* •102-И04, что не противоречит экспериментальным данным. Разброс в значениях коэффициента диффузии обусловлен неточностью имеющих­ся данных о температуре электронов и амбиполярном электрическом по­тенциале. Наряду с этим следует помнить, что полученные нами резуль­таты не могут претендовать на точность большую, чем по порядку величины, так как для упрощения вычислений мы заменили аксиальную симметрию плоской и для учета кулоновских соударений использовали модельное уравнение (5).’

За обсуждение работы авторы благодарны Д. А. Панову, А. П. По - прядухину и В. А. Чуянову.

Поступила в редакцию 12 февраля 1975 г.