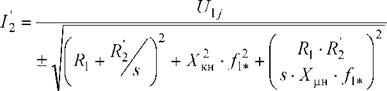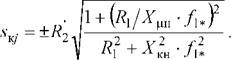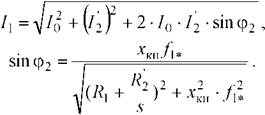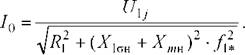Асинхронный электропривод с частотным регулированием угловой скорости
Изменение частоты питающего напряжения асинхронного двигателя влияет как на его синхронную скорость со0, так и на его реактивные сопротивления, которые меняются пропорционально изменению частоты:
Хaj — Хан • fj / fn, Х2Qj — Х2он ' flj! fin 5 Xm — XmH ' fj І /ін 5
где /ін - номинальное значение частоты напряжения статора асинхрон-
і
ного двигателя; Х1он, Х2он - индуктивное сопротивление рассеяния обмотки статора и индуктивное сопротивление рассеяния обмотки ротора, приведенное к обмотке статора при номинальной частоте питающей сети fin-
Если одновременно с частотой fXj изменять и переменное напряжение U j обмоток статора асинхронного двигателя, то появляется возможность реализовать в системах преобразователь частоты - асинхронный двигатель (ПЧ-АД) различные законы регулирования скорости. Для сравнительной оценки этих законов регулирования воспользуемся уравнением баланса мощностей. Мощность на валу двигателя
Р2 =Р-АР2 =(0-(l-s)-M, (5.51)
где Р - электромагнитная мощность, передаваемая от статора к ротору; АР2- мощность потерь в роторе.
Из (5.51) следует, что при любом способе регулирования скорости асинхронного двигателя важно согласовать регулировочные механические характеристики двигателя с его нагрузкой.
По характеру зависимости момента механизма от его скорости -
Мс = /(со) можно выделить следующие механические характеристики
производственных механизмов:
• не зависящая от угловой скорости механическая характеристика
Мс = const; Рс = к • со; (5.52)
• нелинейно-спадающая механическая характеристика или работа с постоянной мощностью
Мс = к • со-1; Рс = const; (5.53)
• нелинейно-возрастающая механическая характеристика или вентиляторная нагрузка
Мс = Ьсо2; Рс = Ьсо3. (5.54)
В частотно-регулируемых электроприводах переменного тока зависимости (5.52)-(5.54) можно сформировать и для электромагнитных моментов двигателей. Например, при постоянном моменте нагрузки (Мс = const) управление напряжением и частотой тока статора асинхронного двигателя должно осуществляться по закону
Uj / fj = const. (5.55)
При нелинейно-спадающей нагрузке Мс = к • со-1 -закон управления напряжением и частотой принимает вид
Uj jfij = const. (5.56)
2
Наконец, при «вентиляторной» нагрузке Мс = к ■ со напряжение и частота должны изменяться в соответствии с зависимостью
^ly//lj2 = const. (5.57)
Законы управления (5.55)-(5.57), связывающие напряжение, частоту и характер нагрузки, описываются формулой М. П. Костенко:
У1'=У*ТЬ1%’ (5'58)
где UiH - номинальное напряжение питающей сети, В; IIj - напряжение на выходе преобразователя частоты; Мс - статический момент на валу асинхронного двигателя при данной частоте.
Из (5.53) следует, что, например, для привода, работающего с постоянной мощностью, увеличение скорости в четыре раза приводит к уменьшению статического момента Мс также в четыре раза. При этом потери в стали и на намагничивание уменьшаются, а перегрузочная способность двигателя остается примерно постоянной:
М/мк= const’ (5-59)
|
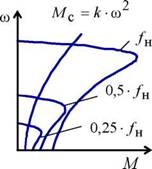
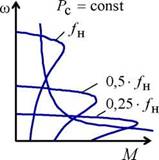
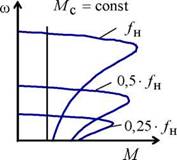
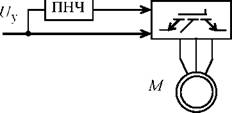
Рис. 5.35. Механические характеристики производственных механизмов и электроприводов преобразователь частоты - асинхронный двигатель Функциональная схема электропривода, выполненного по системе преобразователь частоты - асинхронный двигатель, реализующая различные законы управления класса Uj jfj, приведена на рис. 5.36. |
где Мк - критический момент двигателя, Н • м.
|
|
|
|
|
|
Таким образом, для того, чтобы наиболее эффективно реализовать принципы частотного управления асинхронным двигателем, необходимо в соответствии с видом нагрузки на валу двигателя управлять напряжением, подводимым к статору, взаимосвязано с изменением частоты тока статора. Перечисленные режимы управления достаточны для большинства механизмов. Однако закон управления (5.58) справедлив только в первом аналитическом приближении, когда активным сопротивлением статора Rx можно пренебречь. В действительности, при малых значениях частоты (f< 0,5 • /1н) падение напряжения на сопротивлении Rl существенно снижает величину напряжения, прикладываемого к контуру намагничивания, и критический момент асинхронного двигателя уменьшается. При более точном анализе, учитывающем падение напряжения на сопротивлении R±, механические характеристики принимают вид, показанный на рис. 5.35. Так, например, при законе управления U j j fj = const, предполагающем постоянство критического момента, наблюдается его снижение при уменьшении частоты fx
|
Рис. 5.36. Функциональная схема скалярного частотного управления скоростью асинхронного двигателя |
В этой схеме сигнал управления Uy определяет модуль напряжения статора.
При частотном регулировании скорости асинхронного двигателя необходимо учитывать, что реактивные сопротивления двигателя зависят от частоты питающего напряжения. При снижении частоты / ■ активное сопротивление Ry становится соизмеримым с реактивными сопротивлениями машины, поэтому расчет электромеханических и механических характеристик асинхронного двигателя производится в соответствии с уравнениями, приведенными в [6].
|
|
Электромеханическая характеристика, определяющая зависимость приведенного тока ротора от скольжения,
где Uij - фазное напряжение обмоток статора асинхронного двигателя; /і* = fj //ін - относительное значение частоты питающего напряжения.
|
|
|
A "j/fj = COnSt |
|
Uljlflj = const |
|
= const |
|
0,25 |
|
|
h h, h
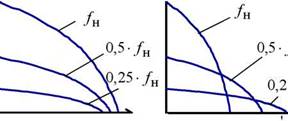
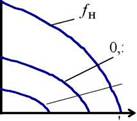
Рис. 5.37. Электромеханические характеристики /0 = /(со) для трех законов регулирования класса Ujj fj
Для короткозамкнутого асинхронного двигателя одной из основных является электромеханическая характеристика = /(со), отражающая зависимость тока статора /от скорости со (скольжения s). Ток статора / определяется путем сложения вектора тока намагничивания
/0 и вектора тока ротора /2 . Обычно это производится с помощью круговой диаграммы. 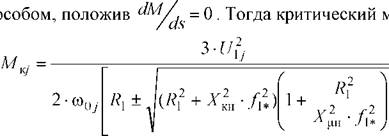
|
Механическая характеристика асинхронного двигателя имеет критический момент и критическое скольжение, которые определяются |
|
обычным спс |
|
момент |
|
(5.64) |
где (Dqj = 2- п - fij jр- синхронная угловая скорость; Ulj - фазное напряжение обмоток статора асинхронного двигателя.
|
|
Критическое скольжение
(5.65)
Знак «+» означает, что критический момент и скольжение относятся к двигательному режиму, знак «-» - к генераторному режиму рекуперативного торможения.
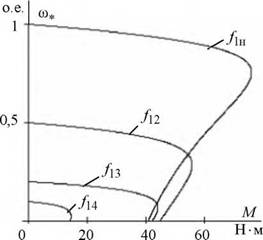
Механические характеристики, рассчитанные по (5.63) в математической системе MathCAD, приведены на рис. 5.39. С целью наглядного представления о регулировании скорости механические характеристики на рисунке приведены в координатах М = /(со*).
|
Рис. 5.39. Механические характеристики асинхронного двигателя типа 4А112МВ6УЗ при частотном регулировании скорости в соответствии с законом регулирования Uj j fj = const |
Анализ характеристик показывает значительное снижение критического момента асинхронного двигателя при частотном регулировании скорости в соответствии с законом регулирования Uj jfj = const.
|
|
|
А |
|
0 |
|
10 |
|
20 |
|
30 |
|
Рис. 5.40. Электромеханические характеристики асинхронного двигателя типа 4А112МВ6УЗ при частотном регулировании скорости в соответствии с законом регулирования UjJ fj = const |
|
|
|
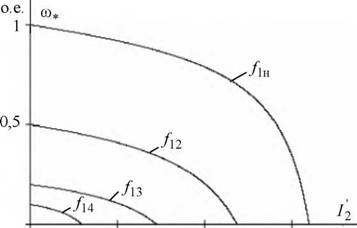
Расчет электромеханических характеристик /, = /(со*) произведем по уравнению (5.61): |
|
где |
Пересчет скольжения s на угловую скорость со для каждой из характеристик проведем в соответствии с выражением со = со0 (1 — s). Так
|
|
как с изменением частоты / ■ и напряжения статора II j ток холостого хода /0 изменяется, то его значение для каждой из частот будем определять по выражению
(5.66)
Как следует из анализа электромеханических характеристик (см. рис. 5.43-5.45), регулирование скорости изменением частоты напряжения статора с законом регулирования Uj jfj = const приводит к значительному уменьшению пусковых токов, а в данном примере, как следствие - к уменьшению допустимого диапазона нагрузок для двигательного режима работы электропривода.
|
Рис. 5.41. Электромеханические характеристики I = /(со*) асинхронного двигателя типа 4А112МВ6УЗ при частотном регулировании скорости в соответствии с законом UjJ fj = const |
Поскольку с увеличением мощности электродвигателя значение сопротивления Ry в относительных единицах уменьшается, то у двигателей большой мощности с уменьшением частоты /j сокращение рабочего диапазона нагрузок происходит в меньшей степени.