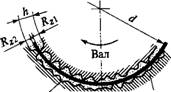
Трение и смазка подшипников скольжения
Режимы трения и критерии расчета. Выше отмечено, что работа трения является основным показателем работоспособности подшипника. Трение определяет износ и нагрев подшипника, а также его КПД. Для уменьшения трения подшипники скольжения смазывают. В зависимости от режима работы подшипника в нем может быть полужидкостное или жидкостное трение. Схематизированное представление об этих режимах дает рис. 16.3.
При жидкостном трении рабочие поверхности вала и вкладыша разделены слоем масла, толщина H которого больше суммы высот Rz шерховатостей поверхностей (на рис. 16.3 разделяющий слой масла изображен толстой линией):
H>Rzl+Ra. (16.1)
При этом условии масло воспринимает внешнюю нагрузку, предотвращая непосредственное соприкасание рабочих поверхностей, т. е. их износ. Сопротивление движению в этом случае определяется только внутренним трением в слое масла. Коэффициент жидкостного трения находится в пределах 0,001...0,005 (что может быть меньше коэффициента трения качения).
При полужидкостном трении условие (16.1) не соблюдается, В подшипнике будет смешанное трение — одновременно жидкостное и граничное. Граничным называют трение, при котором трущиеся поверхности покрыты тончайшей пленкой масла, образовавшейся в результате действия молекулярных сил и химических реакций активных молекул масла и материала вкладыша. Способность масла к образованию граничных пленок (адсорбции) называют мас
лянистостью (липкостью, смачиваемостью). Граничные пленки устойчивы и выдерживают большие давления. Однако в местах сосредоточенного давления они разрушаются, происходит соприкасание чистых Масло Вкладыш поверхностей металлов, их схваты
Вание и отрыв частиц материала при относительном движении. Полужид - Рис. 1б. з костное трение сопровождается из
Носом трущихся поверхностей даже без попадания внешних абразивных частиц. Коэффициент полужидкостного трения зависит не только от качества масла, но также и от материала трущихся поверхностей. Для распространенных антифрикционных материалов коэффициент полужидкостного трения равен 0,008...0,1.
Для работы подшипника самым благоприятным режимом является режим жидкостного трения. Образование режима жидкостного трения является основным критерием расчета большинства подшипников скольжения. При этом одновременно обеспечивается работоспособность по критериям износа и заедания.
Основы теории жидкостного трения. Исследование режима жидкостного трения в подшипниках основано на гидродинамической теории смазки*. Эта теория базируется на решениях дифференциальных уравнений гидродинамики вязкой жидкости, которые связывают давление, скорость и сопротивление взякому сдвигу.
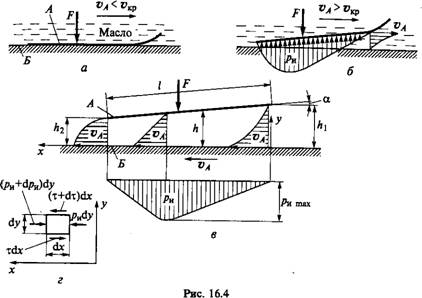
На рис. 16.4 показаны две пластины А и 27, залитые маслом и нагруженные силой F. Пластина А движется относительно пластины 27 со скоростью VA. Если скорость VA мала (рис. 16.4, а), то пластина А выжимает масло с пластины 27. Поверхности пластин непосредственно соприкасаются. При этом образуется полужидкостное трение.
|
|
При достаточно большой скорости VA (рис. 16.4, б) пластина А поднимается в масляном слое и принимает наклонное положение, подобно тому, как поднимаются глиссер или водные лыжи, скользящие по воде.
Между пластинами образуется сужающий зазор, заполненный маслом, а движение происходит в условиях жидкостного трения. Переход к режиму жидкостного трения происходит при некоторой скорости, называемой критической V^. Рассмотрим физику этого явления.
"Основоположником этой теории является Н. П. Петров (1883). В дальнейшем эта теория получила развитие в трудах О. Рейнольдса, Н. Е. Жуковского, С. А. Чаплыгина, А. Зоммерфельда, А. Мичеля и ряда других ученых.
|
|
На рис. 16.4, б в одном из сечений слоя жидкости в зазоре изображена эпюра скоростей жидкости. В граничных точках слоя скорости равны скоростям пластин А и Б. Во всех промежуточных точках скорости меньше скорости VA пластины А. Пластина А набегает на жидкость и прогоняет ее через сужающийся зазор. Этот процесс будет еще яснее, если рассмотреть обращенное движение пластин. Для этого сообщим всей системе обратное движение со скоростью VA. Интересующее нас относительное движение пластин при этом не изменится, но в обращенном движении пластина А остановится, а пластина Б будет двигаться со скоростью VA в обратном направлении (рис. 16.4, в). Эпюры скоростей в обращенном движении изображены на рис. 16.4, в для нескольких сечений. Форма этих эпюр будет обоснована в дальнейшем с помощью соответствующих уравнений. Здесь по направлению скоростей ясно, как жидкость запрессовывается под пластину А и прогоняется через зазор.
Положим далее, что ширина пластины А существенно больше ее длины /ив пределе стремится к бесконечности. Это позволяет пренебречь боковым течением жидкости в зазоре и свести более сложную пространственную задачу к плоской с осями х и у, сохраняя интересующую нас физику явления.
Основополагающим является закон Ньютона
R=/idv/dy;
Где т — напряжение сдвига от внутреннего трения при сдвиге слоев жидкости; Fi — динамическая вязкость жидкости, Па • с; V — скорость течения, м/с.
Закон Ньютона можно рассматривать как аксиому, подобно первому и второму его законам механики. Физический смысл закона можно объяснить так. Два тонких соседних слоя имеют некоторую разность скоростей. На общей границе слоев происходит сдвиг. Сопротивление сдвигу пропорционально интенсивности изменения скоростей в поперечном направлении или производной dv/dy. Коэффициент пропорциональности р зависит от свойств жидкости и определяется экспериментально. Используя этот закон, можно найти все другие характеристики потока жидкости.
Продифференцировав уравнение Ньютона, получим
Dz/dy=pd2v/dy2.
На рис. 16.4, г изображен элементарный объем жидкости со сторонами Dx, dy и Dz=L, а также действующие на него силы в плоскости ху. Из условия равновесия получаем dp^dy^dxdx или D-zjdy—dp^dx. Далее обозначаем dp^Jdx— —G — градиент избыточного давления в зазоре.
После подстановки получим основное уравнение гидродинамики для установившегося двухмерного течения жидкости
D2v/dy2= —G/Р. (16.2)
Интегрируя дважды, получим* V= — Gy2L^2P) + CY+Ci. Постоянные интегрирования Ci и С2 найдем по граничным условиям: при y—Q v—vM при y—h V=0. Опуская промежуточные операции, запишем
V=^Y(H-Y)+VA(J^J, (16.3)
Где h — текущая толщина слоя масла в зазоре.
Объемный расход на единицу ширины пластины равен
Л
Q = ^vdy = Gh 3/(12р)+vAh/2. (16.4)
О
По условию неразрывности потока жидкости величина Q не должна зависеть от х (во всех сечениях зазора Q постоянно). При этом из уравнения (16.4) следует, что градиент давления G должен изменяться с изменением толщины слоя h в соответствии с соотношением
♦Далее используется решение, опубликованное в [6].
DpJdx=-G=6ii(vAlh2-2Qlh3).
Учитывая h=hx — 0Lx, где A — угол наклона пластины А, после интегрирования в пределах от кх до h и граничном условии — при A=Ai Ри=0 — найдем
Уравнения (16.4) и (16.5) можно упростить, имея в виду, что на выходе из пластины, где Л=Л2з избыточное давление ря = 0. Так как постоянный сомножитель в уравнении (16.5) не равен нулю, приравниваем к нулю член в фигурных скобках при Л=Л2 и получаем
<i6-6>
Подставляем (16.6) в уравнение (16.5) и находим
6p, A (hl-h)(h-hj)
H4Hl+hl) ■ (16'7)
Это давление масла в зазоре и уравновешивает внешнюю нагрузку F, а движение пластины А происходит при жидкостном трении. Уравнение (16.7) позволяет построить график давления (рис. 16.4, в). Максимум давления смещен к узкой стороне зазора.
Используя полученные решения, можно сделать следующие выводы.
1. Так как расход Q жидкости одинаков во всех сечениях сужающегося зазора, то средняя скорость течения должна увеличиваться справа налево (рис. 16.4, в). В то же время на границах с пластинами скорости жидкости постоянны и равны скоростям пластин. В сечении, совпадающем с максимумом давлений, dpjdx= —G=0. При этом, согласно уравнению (16.3), скорость v в этом сечении изменяется по линейному закону пропорционально у. Теперь нетрудно понять, что, по условию увеличения средней скорости справа налево, эпюра в сечении H будет вогнутой, а в сечении й2 — выпуклой. Величины скоростей в любом слое и в любом сечении можно рассчитать по уравнению (6.3).
2. Установим зависимость давления от толщины масляного слоя. В среднем сечении A=(AI + A2)/2. При этом после подстановки в (16.7) получим
A
61»л .
|
(16.7а) |
|
Ыср = |
Учитывая малые величины зазоров (несколько мкм) и угла а, приближенно принимаем й2=0 [6]. Тогда
(16.76)
Следовательно, давление обратно пропорционально толщине масляного слоя. В подшипниках эта толщина имеет порядок десятых и сотых долей миллиметра и поэтому давление может достигать очень больших величин.
3. Если угол а наклона пластины А стремится к нулю, то в пределе будет h{=h=h2 и в уравнении (16.7) получим /?и=(00)/0 = = 0. Из этого следует важный вывод о том, что одним из условий образования режима жидкостного трения является наличие сужающегося зазора, который принято называть клиновым.
В нашем примере начальный клиновой зазор образуется с помощью скошенной кромки пластины А. Если конструкция подшипника не имеет клинового зазора, то в подшипнике не может образоваться жидкостное трение. Например, простой плоский подпятник (см. рис. 16.1, б) не имеет клинового зазора и не может работать при жидкостном трении. Для образования клинового зазора, а следовательно, и условий жидкостного трения опорной поверхности подпятника придают специальную форму (см. рис. 16.11).
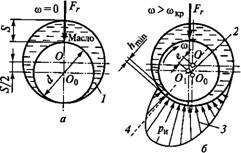
В радиальных подшипниках клиновая форма зазора свойственна самой конструкции подшиПнИка. Она образуется за счет смещения центров цапфы вала и вкладыша (рис. 16.S, а).
При угловой скорости ш>Й),р цапфа всплывает в масле и несколько смещается в сторону вращения по траектории, указанной на рис. 16.5, б. На рис. 16.5, а, б: 1 — клиновой зазор; 2 — путь центра цапфы при увеличении скорости вращения; 3 — эпюра давления в масляном слое; 4 — линия центров. С увеличением угловой скорости увеличивается толщина разделяющего масляного слоя Ащш, а центр цапфы сближается с центром вкладыша. При со—> оо расстояние между центрами Полного совпаде
|
|
Ния центров быть не может, так как при этом нарушается клиновая форма зазора, как одно из условий режима жидкостного трения.
Исследования показывают, что для подшипников с определенными геометрическими параметрами толщина масляного слоя является некоторой функцией характеристики рабочего режима подшипника
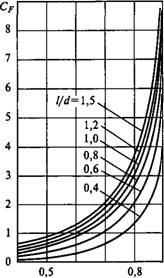
|
0,6 0,7 Рис. 16.6 |
|
0,9 х |
|
30 40 50 60 70 80 90 Г, Рис. 16.7 |
Ашш = Ф (дю/р), (16.8)
Где рсо/р — характеристика рабочего режима подшипника; P=Fr/(Ld)— условное среднее давление в подшипнике, характеризующее нагрузку; / и D — длина и диаметр подшипника.
Характер зависимости (16.8) следует из полученного ранее уравнения (16.76). Здесь отметим только, что толщина масляного слоя возрастает с увеличением вязкости масла и угловой скорости цапфы. С увеличением нагрузки толщина масляного слоя уменьшается.
Таким образом, для образования режима жидкостного трения необходимо соблюдать следующие основные условия■ 1) между скользящими поверхностями должен быть зазор клиновой формы 2) масло соответствующей вязкости должно непрерывно заполнять зазор; 3) скорость относительного движения поверхностей должна быть достаточной для того, чтобы в масляном слое создалось
Давление, способное уравновесить внешнюю нагрузку.
Известно, что все жидкости и газы обладают вязкостью. Это значит, что при определенных
|
Рис. 16.5 |
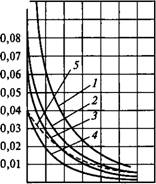
Па - с г 0,09
Условиях в качестве смазывающей жидкости можно применять воду и даже воздух, что и используют на практике.
Режим жидкостного трения нарушается, если величины со и р выходят за допускаемые пределы (например, в периоды пусков и остановов). При переменных режимах нагрузки меняется H^, а следовательно, и положение оси вала. Это может служить причиной вибраций. Достоинства подшипников скольжения по сравнению с подшипниками качения снижаются при переменных режимах нагрузки, частых пусках и остановах.