Детали машин

Относительное движение зубьев, выбор профиля и размеров зубьев

Разработано несколько профилей зубьев для волновых передач. Преимущественное распространение получили эвольвентные зубья, как наиболее технологичные и обеспечивающие удовлетворитель­ное зацепление. При большом числе зубьев волновых передач (обы­чно Z> 150) форма эвольвентного зуба близка к трапецеидальному.

При использовании распространенного двадцатиградусного ис­ходного контура угол профиля & варьируют путем смещения инст­румента при нарезании, приспосабливая его к условиям зацепления. Синтез зацепления выполняют на основе анализа относительного движения зубьев.

На рис. 10.3 изображена траектория движения точки срединной поверхности гибкого колеса. Уравнения этой траектории можйо использовать для построения графика относительного движения зубьев в процессе зацепления.

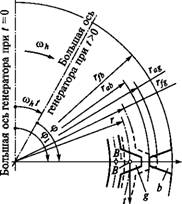
На рис. 10.6 показано взаимное положение зубьев на малой оси генератора в момент времени /=0. Штриховой линией изображено положение зуба колеса G до деформирования. Здесь г — радиус срединной поверхности; ось п совпадает с осями симметрии зубьев; rag, Гаь — радиусы окружностей вершин зубьев; Rfg, — радиусы окружностей впадин.

Положение зуба колеса Ь в осях координат п — T определяем по двум точкам, взятым на оси симметрии и соответствующим окру­жностям вершин и впадин. Координаты по оси п

Wab=Rab~N П/Ъ=Г/Ъ-Г9 По оси t Vab = Vfb = 0.

Положение зуба колеса G изменя­ется при повороте генератора. Теку­щее положение большой оси генера­тора (при />0) определяем углом

Q> = q>x-coht=n/2 - Coht. (10.19) При этом координаты по оси п

Wag=(Tag+W) cos q>b - r,

Wfg=(rfg+w)cos(pb-r;

По оси /

Vag = V + (rag—r)9—(rag--W)(pb9 Vfg=v+(rfg-r)0 -(rfg+n)<Pb-

В формулах (10.21) вторые члены учитывают поворот нормали на угол 0, третьи члены — относительный поворот колес на угол q>b[25].

<Ръ=Co'htlifa = (я/2 - <р)/&. По теории оболочек, E=(V—Dw/D(P)R при

H>=h>0cos2<P, 0=(3wosin2<p)/(4r).

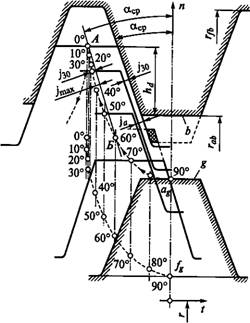
Определение W и V рассмотрено ранее. Расчет координат зубьев (мм) следует выполнять с точностью до пятого знака после запятой, а построение графика взаимного положения зубьев — в масштабе увеличения, например 100:1. Пример графика для ненагруженной передачи изображен на рис. 10.7. На графике две штриховые линии изображают траекторию точек Ag и Fg, соответствующих окружно­стям вершин и впадин зубьев гибкого колеса. Между ними проведе­ны линии осей симметрии зуба. На каждой из этих осей строят профиль зуба, например, через каждые 10° угла ср. Траектории на дуге выхода из зацепления располагаются симметрично. График позволяет отметить, что при эвольвентном профиле зубьев без учета деформации зубьев под нагрузкой в одновременном зацеплении нахо­
дится лишь небольшая часть зубьев в зоне боль­шой оси генератора (ср = =0). На остальной части траектории между зубья­ми существует зазор J. При сравнительно высо­кой податливости гибкого колеса небольшие зазоры под нагрузкой устраняют­ся. В зацеплении вступает большое число зубьев. Чем меньше зазоры в не - нагруженной передаче, тем больше зубьев зацепляет­ся одновременно. Нетруд­но установить, что вели­чины J равны расстояниям между траекторией точки Ag и секущей прямой АБ, Проведенной из точки ср = = 0 параллельно линии профиля зуба колеса Ъ.

Ниже точки Б секущая располагается левее трае­ктории. Здесь вместо зазора образуется натяг или интерференция зубьев при входе в зацепление. Интерференция не допускается. Кроме угла а положение начала интерференции зависит от высоты зубьев. Например, при высоте зубьев, изображенных на рис. 10.7 контурными линиями, интерференции нет. При увеличенной высоте зубьев (штриховые линии) наблюдается интерференция (пересечение головок зубьев заштриховано). Зазоры j и положение точки ин­терференции Б зависят также от формы траектории, которая, в свою очередь, зависит от формы деформирования гибкого колеса (см. ниже).

Толщину зубьев S по дуге произвольного диаметра Dy определя­ют по известной формуле

Sy=dy [n/(2z)+(2Х Tg a )jz+ Inv а+Inv aj,

Где верхние знаки для наружных, а нижние — для внутренних зу­бьев; cos (Xy=Db/Dy (определяют a,); Db=Mz cos a — диаметр основной окружности; inv a, inv ay — эвольвентные углы (см. таблицы, напри­мер [5]).

График (рис. 10.7) используют для выбора основных парамет­ров зацепления: угла а, высоты зубьев, формы и размеров дефор­мирования и пр. Например, в начале построения графика, когда профиль зуба еще не определен, вычерчивают траектории и, зада­ваясь величиной Jmax, проводят секущую АБ. Полученный угол Оср приближенно принимают за средний угол профиля зуба колеса Ъ. По углу аср определяют смещение инструмента при нарезании зубьев:

Xg «(zg/2) (cos a/cos a^ — 1), XbttXg-(m-w0)/m,

Где a=20° — угол исходного контура.

При нарезании долбяком величину хь уточняют на расчете (см. § Ю.7).

При выборе Оср учитывают следующее: зазор ja на входе в заце­пление должен быть достаточным для того, чтобы обеспечить отсутствие интерференции вершин зубьев под нагрузкой (без на­грузки рекомендуют 0,06/и); глубина захода зубьев Hd или высо­та зубьев должны гарантировать сохранение зацепления при дефор­мировании звеньев передачи (гибкого колеса, генератора, жесткого колеса и др.) под максимальной нагрузкой (без нагрузки рекоменду­ют hd^m).

Уменьшение высоты зубьев, необходимое для устранения ин­терференции, можно получить путем уменьшения высоты голо­вок зубьев жесткого и гибкого колес или только одного из колес. При уменьшенной высоте головок соответственно увеличивают­ся радиальные зазоры во впадинах при полной глубине захода зубьев. Следовательно, можно уменьшить высоты ножек зубьев. Нетрудно понять, что уменьшение высоты ножки зуба приво­дит к увеличению ширины впадины по окружности впадин. Увели­чение ширины впадин выгодно для гибкого колеса. Оно приводит к увеличению его гибкости, а вместе с тем и к уменьшению напря­жений изгиба. Рекомендованные профили зубьев изображены на рис. 10.8*. Здесь зубья колеса G имеют только головки, а колеса Ъ соответственно только ножки. Зубья колеса G нарезают модифи­цированным стандартным инструментом с уменьшенной на (0,5...1,0)/и высотой головки режущего зуба. Колесо Ъ нарезают стандартным инструментом при соответственном уменьшении глу­бины врезания.

Условимся называть зубья, нарезанные модифицированным ин­струментом, зубьями с широкой впадиной, а немодифицирован-

"Иванов M. Н., Финогенов В. А., Ромашин В. Н. и др. Авторское свидетельство СССР № 566044.

Ным — зубьями с узкой впадиной. Зубья с широкой впадиной применяют в отече­ственных стандартных передачах.

Большое число зубьев в зацеплении можно получить и в ненагруженной пе­редаче, если профиль зубьев жесткого ко­леса выполнить по форме, эквидистант­ной форме траектории точки Ag (см. рис. 10.7), а профиль зуба гибкого колеса — сопряженным с профилем зуба жесткого колеса. При этом зуб колеса Ъ должен быть выпуклым. Известно, что внутренние эвольвентные зубья имеют вогнутый профиль. Поэтому они не оптимальны для волновых передач.