Кинематика и динамика цепной передачи
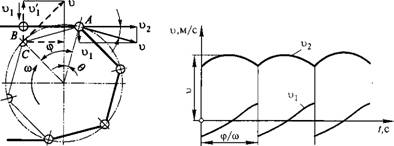
Неравномерность движения и колебания цепи. На рис. 13.8 показаны скорости шарниров цепи и зубьев ведущей звездочки. В данный момент шарнир А находится в зацеплении, а шарнир В приближается к зацеплению с зубом С. Скорость шарнира А равна окружной скорости звездочки v в точке, совпадающей с центром шарнира. Эту скорость можно разложить на составляющие: v2, направленную вдоль ветви цепи, и vx — перпендикулярно цепи.
В зависимости от положения ведущего шарнира составляющие скорости изменяются:
V2=vcos0, vi=vsin0. (13.13)
|
(13.10) |
Здесь угол в изменяется в пределах — ср/+(р/2. Угол (—ср/2) Соответствует моменту входа в зацепление шарнира А, угол (+ ср/2) — шарнира В, a q>=2n/z.
На рис. 13.9 показаны графики изменения скоростей V2 и Vx. Эти скорости являются периодическими функциями времени T, период которых равен (р/со. На графике 0= —ср/2 при T=0, 0=0 при T=Zcp/(2Co) и 0 = Q>/2 при T=Cp/Co.
Движение ведомой звездочки определяется скоростью V2. Периодическое изменение этой скорости обусловливает непостоянство мгновенного передаточного отношения I и дополнительные динамические нагрузки. Со скоростью Vx связаны поперечные колебания ветвей цепи и удары шарниров цепи о зубья звездочки (см. ниже). Колебания и удары в свою очередь также вызывают дополнительные динамические нагрузки.
Формулы (13.13) позволяют отметить, что перечисленные отрицательные кинематические и динамические свойства передачи проявляются тем сильнее, чем меньше число зубьев Z звездочки.
Исследованиями [10] установлено, что при отсутствии резонансных колебаний вредное влияние пульсации скоростей V1Hv2B значительной степени снижается вследствие упругости и провисания цепи. Для рекомендуемых параметров (Г, рц, а и пр.) непостоянство передаточного отношения не превышает 1...2%, а динамические нагрузки составляют несколько процентов от окружной силы Ft. При большинстве режимов работы цепных передач резонансные колебания не наблюдаются, так как частота возмущающих импульсов больше частоты собственных колебаний. Кроме того, амплитуды колебаний уменьшаются вследствие демпфирующих свойств цепи.
|
Где а — межосевое расстояние, м; F — сила натяжения ведущей ветви, Н; Q — масса 1 м длины цепи, кг/м; — в мин"
Рис. 13.9 |
|
Рис. 13.8 |
Для приближенной оценки критической частоты вращения можно использовать формулу
(13.14)
Удар шарнира о зуб и ограничение шага цепи. В момент входа в зацепление шарнира В с зубом С (см. рис. 13.8) вертикальные составляющие их скоростей V и V направлены навстречу друг другу — соприкосновение шарнира с зубом сопровождается ударом. Эффект удара можно оценить потерей кинетической энергии
Ek=0,5Mvy.
Здесь M = Qpn — масса цепи, которая участвует в ударе (приближенно принимают равной массе одного звена); рп — шаг цепи; Vy — скорость удара. В результате преобразований для цепных передач получают [7]
Ek = 0,5Qn?Pl sin2 (3607n ■[Ek (13.15)
Последовательные удары сопровождаются шумом передачи и являются одной из причин разрушения шарниров цепи и зубьев звездочки. В некоторых случаях удары приводят к раскалыванию роликов. Для ограничения вредного влияния ударов, на основе зависимости (13.15), выработаны рекомендации [7] по выбору шага цепи, в зависимости от быстроходности передачи.
Частота вращения п, мин""1:
Роликовые цепи при 15 1250 1000 900 800 630 500 400 300
Зубчатые цепи при ^>17 3300 2650 2200 1650 1320 — — — Наибольший допускаемый шаг
Цепи Fojouut, Мм 12,70 15,87 19,05 25,40 31,75 38,10 44,45 50,80
Примечания: 1. На практике всегда желательно принимать шаг меньше допускаемого. 2. При увеличении частоты вращения за указанные пределы необходимы повышенная точность и обильная смазка передачи.