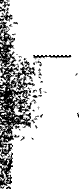АВТОМАТИЗИРОВАННЫЙ ЭЛЕКТРОПРИВОД В ПРОКАТНОМ ПРОИЗВОДСТВЕ
ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
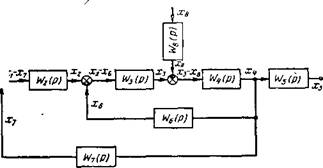
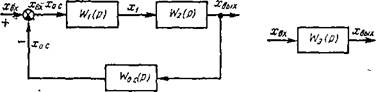
На рис. 5 приведена структурная схема системы регулирования с обратными связями [3]. Здесь и в Дальнейшем входные и выходные величины понимаются как изображения, и для упрощения в написании их знак оператора опускается.
В. рассматриваемой схеме приняты следующие обозначения
Wі (р) — передаточная функция звена в цепи управляющего сигнала;
(р) и W3 (р) — передаточное функции усилительно регулирующих звеньев,
(р) — передаточная функция звеньев объекта регулирования; ч ^5 (Р) — передаточная функция звена в цепи косвенно регулируе
мой величины;
15 v, (p) й ^7 (p) — передаточные функции звеньев в цепях обратной связи;
(р) — передаточная функция звеньев в цепи возмущающего сигнала;
х0 — желаемое значение регулируемой величины;
> I -> Xi — управляющий сигнал,
^ 1 *2 и х3 — выходные величины регулирующих элементов;
х4 — регулируемая величина; х5 — косвенно регулируемая величина;
^ ' хв и х7 — выходные величины элементов обратной связи;
-J _ [*8 — возмущающий сигнал; ц
Хв — возмущающее воздействие.
|
!ИС ^Структурная схема системы регулирования с обратными срязями |
|
|
|
3*0 .. X/ «2 !-*. Щ(Р) - Ц2>. |
|
|
Как отмечалось, в общем случае система автоматического управления представляет сложную многоконтурную систему и имеет более одного входного сиг-
|ала.’' Для упрощения исследования таких систем обычно приводят сложную груктурную схему к эквивалентной более простой или одноконтурной схеме. р*|^ч В линеаризованных системах часто рассматривают действие каждого от - ріельноуо входного сигнала и затем, применяя принцип наложения, находят результирующий эффект от действия различных сигналов. При этом необходимо щомнить, что передаточная функция для каждого входного сигнала зависит от
|
Ё |
аместа действия входных сигналов.
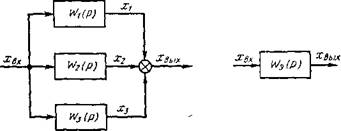
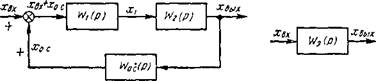
рри упррщении структурных схем участки, состоящие из нескольких звеньев, іе'ня;от эквивалентным звеном, передаточная функция которого определяется основании следующих теорем из теории автоматического регулирования "1. "Передаточная функция звеньев направленного действия, включенных медовательно (рис. 6, а), равна произведению передаточных функций отдель - ^ых звеньев;
(Р)
(Я)
V
2. Передаточная Срис. 7, а) равна;-.
Wi(p) + W2(p) + W9(p). • (131)
функция звеньев с обратной отрицательной связью
|
|
|
|
|
а |
6
Рис 6 Преобразование структурных схем при последовательном (а) н
|
|
|
а |
параллельном (б) соединении звеньев
|
|
б
Рис 7 Преобразование структурных схем при отрицательной (а) и положитесь ной (б) обратной связи
|
4. Передаточная функция звеньев с обратной положительной связью (рис. 7, б) равна |
|
Wi (р) W'» (Р) |
|
*вых (Р)_________________________________________ *вх(р) ” l-W1(p)W2(p)W0.c(p)' |
|
W, (р) = |
|
(1.33) |
|
5. В случае, если линеаризованная система имеет перекрестные связи между звеньями, преобразование системы в одноконтурную производится перенесением |
|
л3 |
|
хг |
|
w,(p) s - іф |
|
ШР) |
|
W3(P) |
|
Хо. а |
|
Xict |
|
Woci(P) |
|
с t (Р) - |
|
■Zfo £Sx~xo. ct |
|
X2 |
|
X) |
|
Xt X/ ~JCo. CZ —► |
|
W, tp) |
|
W2(pl |
|
Uj(P) |
|
Xo. cz |
|
Xj |
|
Xact |
|
Wjlp) |
|
wac2{p) |
|
Wo a(P) |
|
Рис. 8. Преобразование структурной схемы при перекрестных связях между звеньями |
|
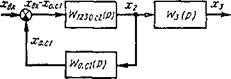
точки подключения одной из перекрещивающихся обратных связей на одно из предыдущих или последующих звеньев. При этом в контур обратной связи включают дополнительные звенья с передаточной функцией, обеспечивающей сохранение уравнений поведения системы. Другими 'словами, при преобразовании структурной схемы линеаризованной системы новая эквивалентная структурная схема должна обеспечивать общий результат поведения системы такой же, как и для первоначальной физической системы (система должна описываться одними и теми же уравнениями). Например, многоконтурная система с двумя перекрещивающимися обратными связями W0.n (р) и Wo. cz (р) (рис.8, а)-может быть преобразована по двум вариантам [4, ^,5]. |
Первый вариант. Заменим звено с передаточной функцией W3 (р) Двумй одинаковыми звеньями, имеющими одну и ту же входную величину, т. е перенесем точку подключения обратной связи звена W0. С2(р) с последовательно включенным звеном (р) с выхода третьего звена на выход второго звена (рис. 8, б).
Дальнейшее упрощение схемы проводят на основании приведенных выше теорем автоматического регулирования.
Заменив часть схемы с звеньями Wx (р), (р), W3 (р) и WQ С2 (р) одним
эквивалентным звеном с передаточной функцией
|
хг |
|
•ч |
|
Щ(Р) |
|
W/(P) |
|
хо с! |
|
Wj(p) |
|
**> ~Хл С2 |
|
|
W2(p) |
|
|
Хр с2 |
|
|
Wo сгІР) |
|
|
Мд СІІР) |
|
Х2 |
|
'E&CXacl |
Мпзш(Р) |
Хз |
|
|
э *■ |
|||
|
Xq С! |
|||
|
Wp a (Р) |
|||
|
Wj(p) |
|
Ха с! |
|
Wizo. c2o. ciW |
1 6 в
Л
Рис. 9. Второй вариант преобразования структурной схемы
_________________ Щ (р) (р)
( 123 °' ЫР) ~ (Хвх-Хо. сі) (Р) ~ Ч - (р) (Р) W0 с 2 (р) ’ U
получим схему, представленную на рис. 8, в.
Заменяя' эту схему одним эквивалентным звеном, получим передаточную, / функцию этого звейа:
W <п — *3 — W 1п ________ ^123 о Clip)____________________ ^
э(Р} ^вх(р)- з(Р) l + W'l«o. c(P)^o. ci (Р) “ , J ________________________ (Р) ^2 (Р) ^3 (Р) ‘ ^ (j 35)
1 + ^2 (Р) W, (Р) »0. С 2 (Р) + W'l (Р) ^2 (Р) Wo. с 1 (Р)
Второй [вариант. Перенесем точку [подключения звена обратной связи W0. ci(p) с выхода второго звена на выход третьего звена. Схема имеет вид, представленный на рис. 9,а. Для этой схемы
U7 ,-л *з (Р)_______________ Щ (Р) ^2 (Р) Г, (р)
123 °- с 2 (Р) ~ (*вх - Хо. с х) (Р) _ 1 + 1^2 (Р) ^3 (Р) с 2 (Р) • ( }
’ Если за выходную величину принять сигнал обратной связи х0. с1, то легко получить замкнутую систему регулирования с единичной отрицательной обратной связью (рис. 9, б), для которой
W M *o. ci (p)__________ tt7! (p)ff, (p) W0.cl(p)
H0.C20.CI ip) {Xbx^Xo ci) {p) l + V2(p)W3(p)W0 ci(p) ■ (L37)
Если зд выходную величину принять сигнал xz, то легко получить замкнутую систему регулирования (рис. 9, в), для которой
Wt (о) _______________ *3 (р)_____________ wi (р) (р) (р) /т оо
о. с а Р) (^x_^cl)(p) l + W2(p)Wi(p)W0:<:2(p) ' ( }
г(
' ^°- с 1 (р) Х0. с I (р) ,т QQ.
^з(Р) ~,,-*з(р) • (1>39)
У
Заменяя .эту схему одним эквивалентным звеном, получим передаточную. функцию этого звенз ' v
rn ___ *3 (р)_____________ ^123 О. С 2 (р)______
Д., *вх (р) X J | П7 / » С 1 (р)
‘ + 123 °- с 2 (Р) " 'Ц73 (/,)
(р) ^2 (р) Ws (р)____________________
s;;; J.+ Vt {р w3 (p) Wo. с 2 (p) + (P) (p) ^o. dip) • ( )
Рассмотренные две структурно преобразованные схемы имеют одну и ту же
^Эквивалентную передаточную функцию, т. е. любая из схем замещения обеспечит _ о. бщнй - результат поведения системы.