Асинхронные электроприводы с векторным управлением
Тригонометрический анализатор (вектор-фильтр) для вычисления направляющих косинусов вектора магнитного потокосцепления
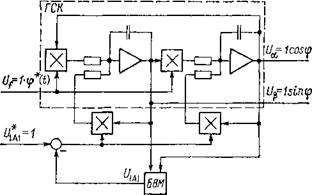
Тригонометрический анализатор ТА строится в виде следящей векторной системы [20, 23], замыкающейся по фазе выходной двухфазной системы напряжений. Управляемым объектом в этой системе является синусно-косинусный генератор с управлением по частоте и амплитуде. Функциональная схема ТА представлена на рис. 1.16. Генератор синусоидальных напряжений работает в режиме постоянного модуля |?| = const и
описывается функцией передачи Y = ехр^/ ^ соч(т)^т^. Тригонометрическое сравнивающее устройство вычисляет значение, пропорциональное | X | sin Дт]; модуль | Y | предполагается равным единице, при малых значениях Дг](^я/6) sin Лт] — Аг], то-
|
1.16. Функциональная схема тригонометрического анализатора |
|
|
|
ж: |
|
РЧи |
|
ГСМ |
|
ж |
|
'шф |
|
ш |
|
|£ |
|
п) X ft— |
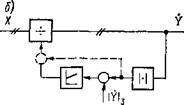
17. Варианты структурных схем тригонометрических анализаторов с П-регулятором (а) с ПИ-регулятором (б)
ч. а передаточную функцию ТА по фазе можно представить
T, z+ 1
|
1.16) |
Ггл(5) =
[VVKl*i)K + 7'i« + 1
1 ле
|
1 |
|
WT(s) = |
|
Т |
|
7-.S+ 1 T2s |
-передаточная функция генератора; mx — масштаб модуля іаодной системы напряжений (целесообразно выбирать так,
1Г0бЫ ГПх | X | max = 1).
Выбор коэффициентов проводим для нормированного no-
її гном а
%(p) = p2 + (Tl/T0)p+ 1, (1.17)
г,—1
і де р — TqS', Т0 — Т-^2Іітх I XI)] ; £20 — Тq Наилучшей настройкой будет TjT2 — 2, тогда
Т і — 2/Т o', Т2 — tnx | X max/(T nQ0) — 1 /(Т rjQo), і де ^ 2 ”
Варианты схем тригонометрического анализатора (ТА) приведены на рис. 1.17 [15]. Упрощенный вариант не использует ГСН. Нормирование по модулю осуществляется при помощи деления входных сигналов на вычисленный модуль. Фильтрация в таком варианте сильно затруднена. Существует отечественная разработка такого анализатора в рамках системы УБСР-АИ [15]—блоки БВА-АИ. Функциональная схема векторного анализатора БВА-АИ приведена на рис. 1.17, а. В схеме БВА-АИ модуль выходного сигнала сравнивается с заданным значением, ошибка подается на вход ПИ-регулятора РЧац,, выход которого является делителем векторного блока деления. Таким образом, сигналы на выходе делителя БВА-АИ оказываются стабилизированными по амплитуде. Улучшающей модификацией векторного анализатора является связь, показанная на схеме рис. 1.17,6 штриховой линией. Тогда при входном сигнале, равном нулю, вследствие очевидного соотношения Y = X/Y, на выходе блока деления сигнал равен нулю. В остальных случаях ПИ-регулятор обеспечивает модулю заданное значение.
Наиболее стабильную работу обеспечивают схемы анализаторов в виде следящей системы на основе управляемых двухфазных генераторов.
В настоящее время разработаны и проверены в эксплуатации надежные схемы генераторов двухфазной системы напряжений [20, 23]. В основу этих генераторов положена симметричная система осциллятора, описываемая системой дифференциальных уравнений
JL дг, = — (ох2; (1.18)
или, переходя к комплексной форме X = Х + №,
= (1.19)
Решая это уравнение, получаем систему, описывающую двухфазные колебания:
X (/) = | X (0) | jcos 15 со (т) dx + arg [* (0)]| +
-f - / sin IJ 0 (t) dx - f - arg [X (0)] }} (1.20)
Для стабилизации характеристик генератора применяются переменные обратные связи у интеграторов, причем знак и коэффициент усиления их определяется ошибкой по модулю выходных напряжений. В этом случае система дифференциальных уравнений принимает вид
4* = МРэ-|*1)* + /ю*. (1.21)
где р3 — заданное значение модуля выходных напряжений.
Рассмотрим анализатор с пропорциональным регулятором частоты. Система описывается дифференциальным уравнением
-%■ X = [к„ (Рз — I X |) + ІК Im (EX')] X, (1.22)
где Е = Е0 + ёг Е0 = exp (ja>n0 ~ выходной сигнал без помех; ёе — exp(jre) — помеха.
Переходя к полярным координатам и учитывая помеху, получим
d (1-23)
ТЬ = К fSln (ті — Чх) + Є Sin (rig — ТІ*)].
Отсюда видно, что модуль выходной системы напряжений не зависит от помехи и искажения возникают только по частоте.
Оценим влияние использования ПИ-регулятора в контуре регулирования фазы. Система дифференциальных уравнений, описывающих такой анализатор, имеет вид:
4г Л* = К [sin (л — riJ + е sin (ле — 11*)] + У,
d (ll24)
-£■ у = ky [sin (л — Лх) + є sin (ле — Л*)].
где у — сигнал на выходе ПИ-регулятора.
Уравнение, определяющее модуль выходной системы напряжений, остается без изменений.
При е = О получаем синусоидальные колебания, причем 11* = Л - Возмущение при є>0 определяются системой дифференциальных у авнений:
•33- 6л* = - ka cos (л - л*) И + ьу + Кг sin (л, - ч£);
JL-6y = - ky cos (л - Л®) и + V sin ( - Л®). (1.25)
При л* — 'П получим
4гь'ь = - + % + К*sin (п. ~ л£);
а (1-26)
~dt ~ ~ kv К + К* sin К - О-
Характеристический полином системы
%{s) = s2 + kas + ky (1.27)
Выбирая ky=(ka,/2)2, получим
%(s) = (s + k(a/ 2)2. (1.28)
При Ащ^2(й>в— со) получим условие сильного подавления высокочастотных помех. Обычно угловая скорость (ое удовлетворяет неравенству
®е >
где z—число зубцов ротора; р— число пар полюсов; со* — частота питания машины.
Заметим, что регулятор частоты целесообразно делать с переменной полосой пропускания в функции значения основной частоты входного сигнала.