Асинхронные электроприводы с векторным управлением

Применение цепей аналитической самонастройки для подавления параметрических возмущений и влияния внутренних перекрестных связей в контурах векторного управления частотно-регулируемых приводов

Основными проблемами при расчете и настройке системы векторного управления являются:

подавление перекрестных связей между каналами управле­ния модулем вектора главного потокосцепления и каналом управления угловой скоростью ротора;

идентификация параметров модели Горева — Парка для кон­кретной машины.

Первая проблема может быть решена путем применения прямой компенсации перекрестной связи, однако коэффициент компенсирующей связи может быть функцией параметра маши­ны и, следовательно, связан со второй проблемой.

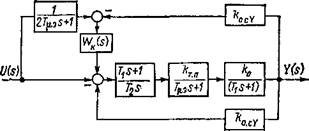
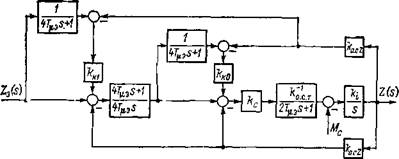
Рассмотрим структурную схему, соответствующую системе подчиненного регулирования (рис. 2.7), где постоянные времени ПИ-регулятора выбраны: ТР=Т; Т2 = 2T^kT. nkak0. с у. Тогда выходной сигнал

Тцэ — эквивалентная постоянная.

Предположим, что истинные значения kT. nk0 отличаются 01 принятых при настройке: (kr. nk0)/(kr. nk0)* = 1 + 6, тогда вы­ходной сигнал системы

Для возмущенной системы

*(«)-{(2г'м>+1Г,-12гг.(1+в)»,+2г'»(1+|»*+1]''>1^7!

F»-(2.37)

Отношение Foi/Fo = 5(1 + б + 662)/(5 4- 36) показывает от­клонение значения средней квадратической ошибки при возму­щении от величины этой ошибки при идеальной настройке. Включение контура с эталонной моделью и корректором с пе­редаточной функцией W'k(s) позволяет подавить параметриче­ские возмущения в контуре.

Используя в качестве корректора регуляторы, применяемые в системах подчиненного регулирования, можно получить эф­фективное подавление параметрических возмущений.

Рассмотрим корректор с передаточной функцией l^K(s) =

27Vas + 1 *

= kK—кг----------------------- • тогда выходная переменная системы будет

Y (s) = { [(2ТМ s + 1] k~YU (s)} X

х{[0+ + <,38)

При отсутствии параметрического возмущения (6=0)

У (s) = {{(27WftK) s + 1] kZ'c. yU (s)} X

X [(■5 + 0 <”> +■)]"• <2-39>

Если заменить в знаменателе полином 2Tl3s2 + + 1 на

полином 27’ll3s+ 1, как это делают при расчете систем подчи­ненного регулирования, то при конечном значении kK> получим

</(*).

т. е. точное соответствие передаточной функции системы мо­дельной.

Интеграл квадрата ошибки при ступенчатом входном воз­действии для возмущенной системы будет

fw=. [(«.+■) С(2„0)

Рв 4 [4ft2 + 13ftK + 10 + 3 (fcK + 2) б] 7-,

и при 6 = 0

(2feK + 1)(*о. е.у^)2

F VE1 (2.41)

р 4(44 + Шк+10)Гйэ

Отсюда при kK > 7/4 и Fp <С F0 для систем с параметриче­ским возмущением получим

Fp6/Fos = {2 (5 + 36) [(1 + 6) (2 + 1/*к) + 6 (6/кк)2]} X

X { [4 + (ІЗ + 36)/6к + 2 (5 + З6)/Рк] (1 + 6 + 662) fcj-i. (242>

Оценивать необходимое значение kK можно, задавая макси­мальное допускаемое значение 6 и выбирая kK таким, чтобы

4fe3 + (Ц+б) k* + (9 + 56) kK - 662 > 0. (2.43)

Применение корректора WK(s)~ kK — пропорционального ре­гулятора — определяет выходной сигнал для невозмущенной системы

У(.)_ [(2У+1)/*к + 1]*о-'с^)

[(2 V + 27^ + l)/kK + 1] (2ГМ» + 1)

и для возмущенной

vM =____________________ [(g^_ + O/^ + iRU^)_____________________ (245)

{ [2Г2э (1+6) в* + 27,цэ(1+ б) s+l]/*K + l} (2Т> + 1) *

Отсюда видно, что с увеличением коэффициента коррекции &к мнимая часть корней полинома 27^3(1 + 6)52+2Гцэ(1 + 6)s + + (&к+1) растет пропорционально V&k+I и одновременно вещественная часть корней уменьшается, что приводит к тео­ретическому возможному резонансу на высоких частотах. К этому же выводу приходим, анализируя интервал квадрата ошибки:

Г _ H + feK)0 + a> + 6621 fe'cy^)2 ,9

8 (5 + 2feK + 36) Т’р. э •

Действительно, при feK 00 получаем

^Пв оо “*■ 16^ (ко. С yU)2,

что при 6 = 0 дает /^пвоо = (^сг^)2/(16Гцэ). Эта величина по сравнению с F0 существенно больше: Fa& oo/Fo = 5/2.

Заметим, что если коэффициент Г2< 2Tll3k0kr. nk0_cY и —1 < < 6 < 0, то при больших значениях kK интеграл квадрата ошибки может быть снижен до приемлемого значения. Таким образом, при использовании пропорционального корректора ко­эффициенты основного ПИ-регулятора контура должны быть увеличены по сравнению с коэффициентами при стандартной настройке.

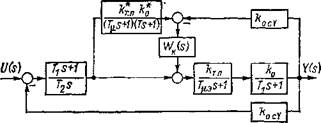
Контур с эталонной моделью мо_жет замыкаться и после основного ПИ-регулятора, в этом случае он служит для форми­рования желаемой передаточной функции объекта (рис. 2.8).

Свертка контура с эталонной моделью вида Wu (s) — (Tl3s + l)-IX X (Tis + l)-1 дает

у M [(Гк2^к) (О + 1) ( + 1) + Txls + 1] У (S)

W (Гщя/ЛО^+ІХГів+П + Гк. в+І £'(Sh

где WK(s) = kK{TKls + 1 )/(TK2s). Из этого выражения видно, что, выбирая 7’к1>7'1 и kK >■ 1, получим У (s) WM (s)Z (s). Коэф­фициент kK может быть выбран достаточно большим без опас­ности возникновения резонанса.

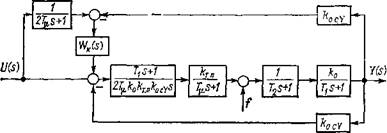
Контур с эталонной моделью может осуществлять подавле­ние помехи (перекрестной связи в системе векторного управ­ления). Структурная схема такой системы приведены на рис. 2.9. Возмущение выходного сигнала

M'(S) = [47>*(7;S + l)tj (s)(T, s+ 1)-‘]Х

Х{ 6. [(/■// + ?■, + ?>+ 1)(47'і/)/6.+27'„ЬІ!»+ l]

(2.48)

Отсюда видно, что подавление низкочастотных помех про­исходит достаточно эффективно, причем коэффициент ослабле­ния пропорционален kK.

Однако заметим, что kK не может быть очень большим, так как может возникнуть неустойчивость:

(Т2+Т„1

К<2-

Здесь существенным оказался учет малых постоянных времени Гг и Гр,, которые при расчетах управляющего воздействия были заменены эквивалентной постоянной времени ГцЭ. Отсюда сле­дует, что при применении контура с эталонной моделью необ­ходимо проверять систему на устойчивость.

Подавление перекрестных связей можно осуществить более эффективно, воспользовавшись основной идеей систем подчинен­ного регулирования. Существо метода состоит в том, что контур по переменной К (рис. 2.10) охватывается еще одним контуром по этой же переменной, причем в контуре используется ПИ-ре - гулятор:

Гр^^г^+щгг^).

Тогда возмущение

(V +1) (7’1S + 1)”1 w _ (250)

6Y (s) = __________________________________________

[(V/ + + Ч * +1] 4 V + +1

Это выражение можно аппроксимировать:

kj(s)

6 Y(S):

(27-(l, s+ I)2 (7s+l) '

Охват цепочкой из N контуров с идентичными регуляторами обеспечивает возмущение в виде

(2 T^s)N kj(s)

(гг^+і)" (r^+l)

Такая структура соответствует оптимальному подавлению возмущений.

Стабилизация передаточной функции при дрейфе или неточ­ном знании коэффициентов осуществляется при помощи контура с эталонной моделью.

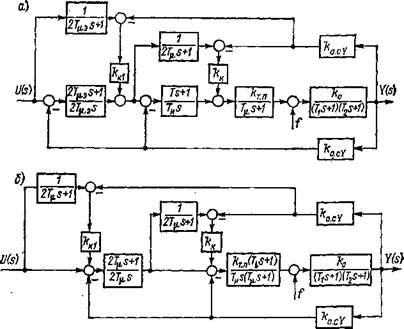
Использование цепочечного регулятора в комбинации с кон­туром с эталонной моделью позволяет полностью решить задачи подавления возмущения и дрейфа параметров. На рис. 2.11 при­ведена схема с однозвенным цепочечным регулятором. Схема

рис. 2.11, а определяется тем, что сигнал контура с эталонной моделью вводится в сумме с сигналом ПИ-регулятора. Полагая передаточную функцию корректора WK(s)=kк, получим

Y (s) = {[(T[S + 1) (2T^s + 1) + 27'»3skK] ft" с уU (s)} X X{([2^9s(V+ 1)(7’2s+ 1)+ l](TiS+ l)+2Tll3skK)(2T}l3s+l)}-'-, 6F(s) = [27'tl3s(V+ 1)]X X {([27V9s (7> + l)(T2s + l) + 1] (7> + 1) + 2T^skK)}'1 f (s).

(2.52)

Схема рис. 2.11,6 характеризуется тем, что сигнал контура с эталонной моделью вводится на вход ПИ-регулятора и тогда

Y(s) — {12Г(ив/(Лк + 1)] (Г(1в + 1) (Г#а + 1) + 1} (2Г(із* + 1) ’

ду / __________ [2^3S/(feк *)] (V ___________________ feO f /

or w— [2Til3s/(kK + 1)] (V + !) (Г* + 1) + 1 (Гі« + 1) '

Сравнение полученных соотношений показывает, что необ* ходимо выходной сигнал контура с эталонной моделью подавать на вход ПИ-регулятора.

Систематическое применение цепочечных регуляторов позво­ляет осуществить настройку контура регулирования угловой скоростью, не используя настройку по симметричному оптимуму. На рис. 2.12 приведена схема контура регулирования угловой скоростью с одиночным цепочечным (одно звено) регулятором. Главный контур имеет П-регулятор, обеспечивающий настройку по техническому оптимуму, с коэффициентами, определяемыми на основании наиболее вероятных параметров канала. Контур тока с использованием цепочечных регуляторов имеет переда­точную функцию

W, (s) = fto. cy/(27'|ws + 1). (2.54]

Внутренний контур регулирования имеет контур с эталонной моделью:

1Р-о(®)=1/(47>+1). (2.55)

Выходной сигнал контура Z (s) = {([47V/(/eK0 + 1)1 s + 1) ([47V3/(feKl + I) ] s + 1) X

x w) {[ * Gctt * + от-s + 0 +

+тетт5+‘]<4Г>“8+,)} 1 (2'56)

и возмущение

bZ (s) = - {[4TuJ(kK0 + 1)] [4TJ{kKl + 1 )]s (2T^s + 1) ktMc (s)} X

y(f z( Кэ * і 47»3 1 А і 4Г*э s і іІГ1

X1L*K1 + 1 V»M + 1 + ftKo+l S+ V+ feKo + l + J) '

(2.57)

Для рассматриваемого случая и N цепочечных контуров

Па47’^+')]*+о

Z(s) — — ГТТлт Тп ^s(s); (2.58)

Xjv+2 (а) (47^ + 1) 3W’ v '

(2 V + ') П [4r^V(*K/ + Щ (4 V^o + ')] ki bZ (s) =---------------- ^m Afc (s), (2.59)

где xjv+2(5) удовлетворяет рекуррентным уравнениям

AT s AT

%N+2(s)==~il %JV+1 (s) + ~k ДЭ+ 1 S +

(2-60)

Заметим, что выбирая &Ki ^ kK2 ^ ... ^kKn, можно обес­печить распределение N корней в области частот, больших 1/(2Гдэ), что позволяет ПОНИЗИТЬ порядок полинома %at+2(s) до N + 1 и пренебречь форсирующим полиномом в возмущении (2T^s +1), тогда

її [4 V/(*Ki + »)] Г4 ГЛ + ‘И kiMс <*>

6Z(s)~--^----------------------------- 5-------------------------------------------- . (2.61)

n[4V(feKi + 1))s + 1

J-о

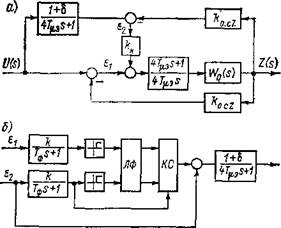
Критическим параметром цепочечного регулятора является коэффициент усиления модели, так как при этом возникает не­соответствие ошибок по основному контуру и контуру с эталон­ной моделью. В результате возникает статическая ошибка, про­порциональная погрешности коэффициента передачи модели (рис. 2.13, а). Здесь Wo(s) — ko.[czPoa{s)JPab(s),

z (s) = {Роа (s) [(47W(1 + (1 + б) ftB)J S + I) [1 + (1 + 6) kK] k~[Z} X X {{[47W(*K + 1)] sPob (S) + (47V3s + l)P0a («)} (1 + A^)}-1 Z3(s),

(2.62)

0 4* ГГ I - j“ (І 6) kj( 1 I

и суммарный коэффициент контура д== r_L~fe = 1 +

і “1“ «к

+ yq^-—8-»■ 1 + 6, feK->oo.

При высоких требованиях к точности привода проблема мо­жет быть решена применением схемы автоматического управ-

ления усилением (АРУ), подстраивающей коэффициент усиле­ния модели в зависимости от знаков ошибок еі и г2. Простая схема АРУ приведена на рис. 2.13,6. При неравенстве сигна­лов ei и 82 их знаки различны. В схеме при помощи фильтров с большими постоянными времени Тф подавляются составляю­щие с частотами переходных процессов. Логические функции ЛФ определяют знаки (єієг С 0), а ключевая схема КС вклю­чает ВХОДЫ либо --kz2, либо —ke2-

Таким образом, для исключения влияния параметрических возмущений привода можно использовать цепочечные регуля­торы для «сильной» развязки каналов и подавления возмуще­ний, замыкая выход контура с эталонной моделью на вход ПИ-регулятора, а при слабых параметрических возмущениях — на выход ПИ-регулятора.