ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА КЛАССИФИКАЦИИ
Для учета воздействия вибрации предложено использовать модифицированную ячеечную модель [25, 26].
Поднимающийся слой полидисперсного материала делится на ячейки концентрическими окружностями с постоянной разницей радиусов и радиальными сечениями с постоянной разницей в углах. Каждый подслой дополняется ячейками, находящимися в скатывающемся слое. В результате такого разделения получается ряд замкнутых подслоев. Ячейки, находящиеся в одном подслое, имеют одинаковые объемы, но по подслоям, объемы ячеек разные.
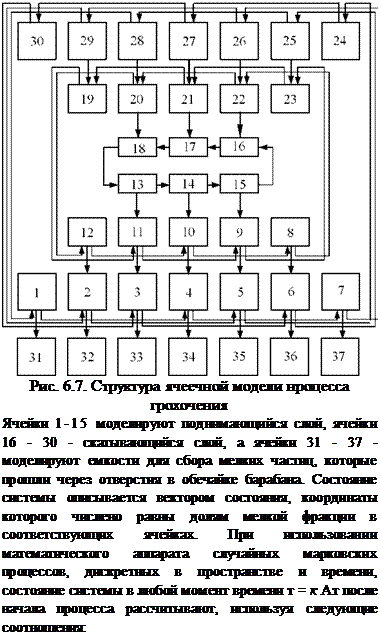
На рис. 6.7 в развернутом виде дана схема соединения ячеек.
где Ат - время одного перехода; 5(A) - вектор состояния системы после перехода к, Р - матрица переходных вероятностей.
При к= 0, т. е. в самом начале процесса можно считать, что мелкие частицы равномерно распределены по всему объему материала, т. е. концентрации этих частиц во всех ячейках будут равны.
Элемент Pjj матрицы переходных вероятностей Р численно равен вероятности перехода мелких
частиц из ячейки і в ячейку j. Численные значения определяются при идентификации параметров математической модели.
Традиционно в математических моделях, построенных на закономерностях марковских цепей, все ячейки имеют одинаковый объем. В рассматриваемой модели ячейки имеют одинаковый объем только в пределах каждого подслоя, но по подслоям эти объемы разные. Эту проблему предложено решить путем умножения вероятностей Р1} на масштабные коэффициенты к1Г которые численно равны отношению объема ячейки і к объему ячейки j.
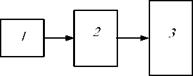 |
Рассмотрим предлагаемый вариант на элементарном примере. Пусть имеется цепь из трех ячеек с объемами 7, 2и J, как это показано на рис. 6.8.
Рис. 6.8. День из трех ячеек с разными объемами
Загрузим в первую ячейку ключевой компонент с объемом, равным 1, тогда вектор начального состояния будет иметь вид 5(0) = (1; 0; 0}. Допустим, что вероятности перехода ключевого компонента из ячейки 1 в ячейку 2 и из ячейки 2 в ячейку 3 равны 0,5. В этом случае стандартная матрица переходных вероятностей имеет вид:
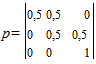 (6.16)
(6.16)
Если пользоваться этой матрицей, то получим:
Д1) = (0,5; 0,5; 0}; 5(2) = {0,25; 0,5; 0,25}.
Совершенно очевидно, что для ячеек разного объема это неверное решение. Действительно, с учетом объемов ячеек мы получим, что объем ключевого компонента равен 2, в действительности этот объем равен 1.
В предлагаемом варианте ki = 0,3, а С. з = 0,666. Матрица переходных вероятностей будет иметь следующий вид:
Если использовать данную матрицу, то получим
ОД = {0,5; 0,25; 0}; 5(2) = {0,25; 0,25; 0,08333}.
Учитывая, что объем ключевого компонента в каждой ячейке равен произведению объема этой ячейки на концентрацию ключевого компонента, можно увидеть, что во всех случаях объем ключевого компонента остается неизменным и равным 1.
Следует отметить, что использование масштабных коэффициентов без ограничений возможно только в тех случаях, когда происходит переход частиц ключевого компонента из ячеек меньшего объема в ячейки с большим объемом. В обратном случае возможны варианты, при которых концентрация ключевого компонента в ячейке станет больше 1, что с физической точки зрения невозможно.
Таким образом, для моделирования процесса смешивания - сегрегации можно использовать традиционную матрицу переходных вероятностей, дополненную масштабными коэффициентами.
В реальном грохоте зернистый материал постоянно находится в движении, и как отмечалось ранее, происходит угловое смещение ячеек.
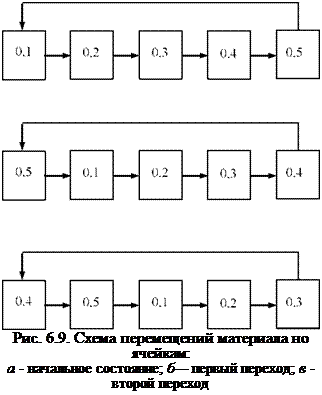 а)
а)
б) в)
Угловое смещение ячеек, т. е. движение сыпучего материала в поперечном сечении, можно имитировать путем умножения, на каждом переходе, вектора предыдущего состояния системы не только на матрицу переходных вероятностей, но и на матрицу перемещений. Элементы матрицы перемещений равны либо нулю, либо единице.
Рассмотрим имитацию движения на элементарном примере. Пусть имеется замкнутый циркуляционный контур, состоящий из пяти ячеек, как показано на рис. 6.9.
Известен вектор начального состояния, например
ДО) ={0,1; 0,2; 0,3; 0,4; 0,5},
т. е. в первой ячейке объем мелких частиц составляет 0,1 от общего объема, во второй - 0,2 и т. д. Пусть за один переход в системе происходит перемещение на одну ячейку слева направо. В этом случае матрица перемещений имеет следующий вид:

![]() (6.18)
(6.18)
После первого перехода вектор состояния будет равен
5(1) = 5(0) Р= {0,5; 0,1; 0,2; 0,3; 0,4}.
Как видно из вектора, произошло перемещение ячеек на одну слева направо.
Рассмотрим теперь наш случай. Пусть материал во внешнем циркуляционном подслое (ячейки 1-7 и 24 - 30) за один переход перемещаются на три ячейки, в среднем подслое (ячейки 8 — 12и19 — 23) — на две ячейки, а во внутреннем подслое (ячейки 13 - 18) - на одну ячейку. В этом случае вероятности
|
Рп 1,4 - |
Рпз 2,5 = |
Рщ 3,6 ~ Рщ 4,7 — Рщ 5,30 |
- Рщ 6: |
,29 |
- Pml,: |
28 = |
||
|
= Рш |
30,27 : |
= Рщ 29, 26 |
= Рщ 28,25 |
= Рщ 27, 24 = |
Pm 26,1 |
— Рпз 25,2 : |
= Рш 24,3 = |
|
|
= Рт |
8,10 = |
- Рпз 9,11 = |
: Рщ 10,12 = |
Рщ 11,23 = Рщ |
12,22 = |
Рш |
23,21 ~~ |
Pm 22, 20 = |
|
= Рш |
21,19 |
= Рщ 20,8 |
= Рщ 19,9 = |
Рщ 13,14 = Рщ |
1 14,15 = |
Pm |
15,18 = |
Рщ 18,17 = |
|
= Рш |
17,16 |
= Рщ 16,13 |
= 1 , |
а оставшиеся вероятности Р„,у и Р„, L J равны нулю.
Таким образом, чтобы получить вектор состояния системы после /-го перехода, необходимо проделать следующие операции:
S' (/) = S(j - )РS(j) = S' (i)Pm, (6.19)
где S' (/) - вспомогательный вектор состояния на переходе /'; Р— матрица переходных вероятностей; Рт - матрица перемещений.
Образование дополнительных частиц мелкой фракции за счет самоизмельчения частиц крупной фракции можно учитывать следующим образом. Концентрация крупной фракции на любом переходе в любой ячейке определяется по одной и той же формуле:
скр(а)=-ф, к). (6.20)
Умножив концентрацию крупной фракции на коэффициент Казм, получим второе слагаемое в формуле (2.37). Таким образом, можно на каждом переходе, используя вспомогательный вектор S состояния системы, у которого все элементы равны единице, проделать следующие операции:
ад=ад+[з-5(*КзМ. (6.21)
В данном случае не требуется ни каких масштабных переходов, поскольку преобразования осуществляются в пределах одной и той же ячейки.
Сделаем допущение о том, что отсев мелких частиц осуществляется только из ячеек, непосредственно контактирующих с просеивающей поверхностью барабана. Для рассматриваемого примера это ячейки 1 - 7 на рис. 6.7. Поскольку объем мелкой фракции, который отсеивается из ячейки і на переходе к, однозначно зависит от концентрации мелкой фракции в данной ячейке, нет необходимости создавать дополнительную матрицу, а вероятности отсева, как вероятности перехода частиц мелкой фракции из ячейки і в ячейку /, с учетом масштабных коэффициентов следует внести в матрицу переходных вероятностей. Если объем каждой ячейки, в которую высыпаются из барабана мелкие частицы, обозначить Vo, то суммарный объем мелких частиц, высыпавшихся из барабана после перехода к., можно рассчитать по следующей формуле:
Фактически уравнения, приведенные в данном разделе, являются математической моделью процесса грохочения. Модель используется следующим образом: рассчитываются параметры распределения сыпучего материала в поперечном сечении барабана; составляется цепь Маркова; по гранулометрическому составу исходного материала формируется вектор начального состояния; рассчитываются масштабные коэффициенты; по известным вероятностям переходов мелких частиц из одних ячеек в другие формируется матрица переходных вероятностей, включающая в себя масштабные коэффициенты; формируется матрица перемещений; производится последовательное перемножение вектора состояния на транспонированные матрицы переходных вероятностей и матрицы перемещений:
У (1) = Х(0)Д S" (1) = У (l)Pm, S( 1) = 5" (1) + [5*1 - S' (ІЖизм];
У (2) = S(l)P, S' (2) = S (2)Pm, S(2) = S' (2) + [Si - 5" (2)A;,M];
S (/) = S(i - )P S' (/) = У (i)Pnh S(i) = S' (/) + [5*1 - S' (/Ж„зм],
где S (/), S' (/) - вектора промежуточных состояний системы на переходе /; У - вспомогательный вектор; Р- матрица переходных вероятностей; Рт - матрица перемещений.
При идентификации параметров математической модели вероятности переходов частиц из одних ячеек в другие при первом расчете принимают равными 0,1, при второй итерации изменяют в нужную сторону.
Имитационная модель процесса грохочения представляет совокупность математических моделей движения, смешивания, сегрегации и грохочения. Кроме этого, введены генераторы случайных чисел и соответствующие фильтры, что позволяет имитировать отклонения параметров от их средних значений (например, отклонения углов трения покоя и движения). Имитационная модель позволяет не только рассчитывать, но и оптимизировать режимные и геометрические параметры.