ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

СМЕШИВАНИЕ В ПОПЕРЕЧНОМ СЕЧЕНИИ БАРАБАНА

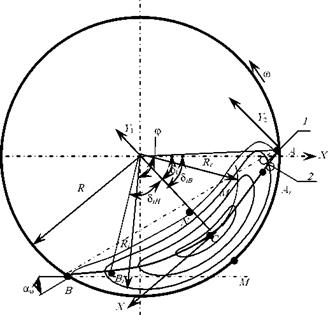
Ячеечпая модель процесса смешивапия. Рассмотрим поперечное сечение гладкого вращающего­ся барабана на у-м участке, частично заполненного материалом (см. рис. 4.1). Параметры, характери­зующие распределение сыпучего материала, в частности, координаты точек А, В, С' определим по

зависимостям (2.19 - 2.21, 2.30), приведенным в гл. 2. Разделим весь материал на подслои и определим их количество:

где dmах - максимальный диаметр смешиваемых частиц.

Найдем границы раздела подслоев Rc. из условия равенства производительности по подслоям. Об­щая объемная производительность по поднимающемуся слою, т. е. объем материала, переходящий из поднимающегося слоя в скатывающийся за единицу времени при единичной длине барабана, равна:

Производительность одного подслоя будет В 11 раз меньше, т. е.

ю(тг2-д?)

4 2 п

С учетом (4.10) для подслоя і можно записать:

Для первого подслоя R = R. Изменяя і от 1 до и, по формуле (4.11) можно определить границы для всех подслоев. Найдем объемы поднимающихся подслоев:

Уш = 0,5~ 82/), (4.12)

где 5Ь, b2l - углы, характеризующие точки перехода частиц из слоя в слой (см. рис. 2.2).

Значение угла 81У определим по формуле

Для нахождения численного значения угла 82У необходимо решить уравнение нижнего участка границы раздела слоев СВ в системе координат ХСУ при щ =0,5(Д + ^_1)sin82y и

ух = Rcos bI - 0,5(Д + ) cos 82У.

После преобразований получим:

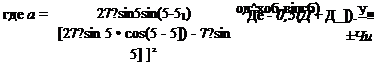Подставив выражения (4.13), (4.14) в уравнение (4.12), можно найти объем любого /-го поднимаю­щегося подслоя. Учитывая конфигурацию скатывающегося слоя, сделаем допущение о том, что по ска­тывающимся подслоям материал распределяется прямо пропорционально объемам поднимающихся подслоев. Общий объем /-го подслоя будет равен:

Пусть общее количество ячеек в системе равно К, тогда объем одной ячейки равен V= 0.5R2L(2b-sm2b)lК и в 1-м подслое будет Njячеек.

Отметим, что значения N,- необходимо округлить до целых чисел. С учетом производительности подслоя (4.10) время одного перехода Ат равно

Ах = Vjq.

Зная начальное распределение ключевого компонента по зависимостям (4.1), можно рассчитать со­стояние системы в любой момент времени X = тАх.

Использование предлагаемой модели для расчета процесса смешивания сыпучих материалов рас­смотрим на конкретном примере, приведенном в разд. 4.1 (см. рис. 4.3). Для определения вероятностей переходов частиц из слоя в слой воспользуемся в данном случае упрощенными формулами: приу > / Pjj= C7;in_i(0,333-Д) +Д; (4.16)

при j<i /'. о. ЗЗ. У'., . (4.17)

Д = 1-Д7-Д), (4.18)

(4-19)

где К0, Кк - плотность материала частиц основного и ключевого компонентов.

Формулы (4.16) - (4.19) полностью учитывают качественную сторону процессов смешивания и сегрегации. Так, при увеличении отношения плотностей увеличивается склонность к сегрегации, а при их равенстве все вероятности равны, что соответствует специфике смешивания сыпучих материалов во вращающемся барабане.

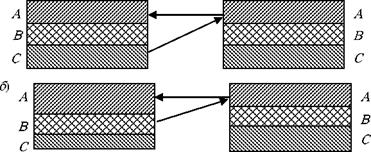
Итак, пусть циркуляционный контур состоит из четырех подслоев и количество элементарных объ­емов в каждом подслое: N = 5; N2 = 4; N3 = 3; Л4 = 2. Представим циркуляционный контур в разверну­том виде (рис. 4.3, а) и введем единую нумерацию объемов. Пусть в начальный момент времени, т. е. при т = 0, С = С2 = Сз = 1 , а в остальных объемах ключевой компонент отсутствует. Вектор начально­го состояния системы будет иметь вид: Д0) = {1; 1; 1; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0}

Очевидно, что при т = 1 в зону смешивания перейдут первые объемы каждого подслоя, т. е. при еди­ной нумерации это объемы 1, 6, 10, 13. Определим элементы матрицы переходных вероятностей. Если плотность ключевого компонента в два раза больше плотности основного, а размеры частиц равны, то по формуле (4.19) значение Pq будет равно 0,670, по формуле (4.16) получим 6 = 0,33, по уравнению (4.17) - Д, і = 0,33, а по выражению (4.18) - Д, і = 0,67 и Д; 6 = 0,67. Для первого перехода остальные вероятности Д у = 1, a Pjj = 0.

Матрица будет иметь вид Д:

Д1) = {0,67; 1; 1; 0; 0; 0,33; 0; 0;0;0; 0; 0; 0; О}. Состояние системы после первого перехода показано на рис.

4.3, б. Аналогично рассчитываются состояния системы на последующих переходах. Пусть т = 6. Перед данным переходом состояние системы определяется вектором

Е(5) = {0,33; 0,33; 0,33; 0; 0; 0,22; 0,67; 0,67; 0; 0; 0,44; 0; 0; О}.

По формуле (4.4) вычислим номера объемов, участвующих в обмене частицами при данном пере­ходе:

щ =6-5 entier[(6 -1)/5] = 1;

«2 = 5 + {б - 4 entier[(6 -1)/4]} = 7; щ = 9 + {6 - 3 entier[(6 -1)/3]} = 12 ; и4 = 12 + {6 - 2 entier[(6 -1)/2]} = 14.

Далее по формуле (4.16) определим Д; і = 0,55; Д; 12 = 0,67. По уравнению (4.17) Д2, і = 0,22. Так как С2 и Си равны нулю, принимаем Д2, и = 0 и Ри, 12 = 0. Тогда по выражению (4.18) Д = 0,45; Д 7 = 0,11; Д212 = 0,78. Следовательно, остальные вероятности Д; у = 1, a Д;7 =0. Матрица переходных веро­ятностей будет иметь вид Д:

Перемножив вектор Д5) на Д, получим

Таким образом, изменяя т и зная время, за которое происходит одни переход, можно последова­тельно определить состояние системы в любой момент времени.

Как видно из сравнения, матрицы Р и Д имеют разный вид на разных переходах, что позволяет учитывать наличие двух слоев в замкнутом циркуляционном контуре - поднимающегося и скатываю­щегося.

Экспериментальную проверку предлагаемой модели проводили на лабораторном барабане диамет­ром 0,6 м. Ключевой компонент загружали в один или несколько элементарных объемов (см. рис. 4.2, двойная штриховка). Барабан приводили во вращение и по истечении определенного времени оценива­ли качество смеси. В качестве критерия оценки был выбран коэффициент неоднородности [7]:

где Д(т) - концентрация ключевого компонента в 1-м элементарном объеме в момент времени т.

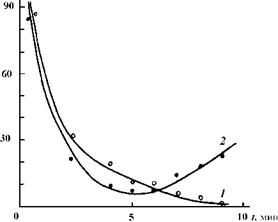
На рис. 4.4 показаны характерные результаты сравнения экспериментальных данных и рассчитан­ных на ЭВМ по предлагаемой модели. Кривая 1 - теоретическая зависимость коэффициента неодно­родности V от времени смешивания для компонентов, отличающихся только по цвету, а кривая 2- для компонентов с частицами одинаковых диаметров, но с плотностями, отличающимися в два раза.

V, %

п = CN/Этах . (4.21)

где <7тах - максимальный из диаметров смешиваемых компонентов.

Рис. 4.5. Схема к определепию параметров движепия сыпучего материала

На практике применение этой формулы в большинстве случаев (кроме случаев кратности величин CNи с1тл,. ) дает дробный результат. В дальнейших расчетах нельзя использовать дробное число подсло­ев, участвующих в процессе смешивания, поэтому в качестве числа подслоев используется целая часть полученного числа, а оставшаяся дробная часть равномерно распределяется между всеми подслоями.

Далее по известной методике рассчитываются параметры подслоев, их границы, производится де­ление подслоев на ячейки и определяется время одного перехода [24, 25].

Поскольку смешивание компонентов происходит только при их движении в скатывающемся слое и носит вероятностный характер, по аналогии с математическим аппаратом случайных марковских про­цессов, дискретных в пространстве и времени, считаем, что состояние системы, т. е. концентрация ком­понентов в подслоях, изменяется скачкообразно. Время одного перехода (скачка) Ат равно отрезку вре­мени, за который границу раздела слоев АС (рис. 4.5) пересекают по одному элементарному объему ка­ждого подслоя. Таким образом, для того чтобы рассчитать состояние системы в момент времени т, не­обходимо последовательно рассмотреть изменения концентрации ключевых компонентов за к перехо­дов, где 1=т/Дт. Следует особо отметить, что на каждом переходе последовательно реализуются опи­санные выше фазы обмена частицами ключевых компонентов между всеми ячейками, а количество этих фаз зависит от числа смешиваемых компонентов.

Использование ячеечной модели приготовления многокомпонентных смесей разберем на примере получения трехкомпонентной смеси с использованием механизма процесса сегрегации, изложенного в первом разделе этой главы.

Для характеристики содержания всех трех компонентов в одной ячейке необходимо использовать понятие концентрации каждого из компонентов в ячейке [25]. Для трехкомпонентной смеси достаточно использовать величины концентраций двух из них с}1’™* и сС'”'. Концентрацию третьего компонента в ячейке і в момент времени х = тАх можно определить по зависимости:

с3[,’т) = 1 - (с;ы + С, Ы), (4.22)

где т= 1,2,...Д.

Поэтому, хотя эта концентрация и не будет представлена в формировании матриц, определяющих концентрации компонентов в каждой из ячеек, ее величину для каждой ячейки всегда будет несложно определить.

Для успешного функционирования модели потребуются также коэффициенты Л); 2, Л); 3, Л)2 3, оп­ределяющие вероятность перехода одного из компонентов в ячейку, лежащую ближе к центру циркуля­ции и содержащую другой компонент.

Первоначальное состояние системы, т. е. содержание исходных компонентов в каждой из ячеек, оп­ределяется характером и последовательностью их загрузки в смеситель.

В процессе обмена частицами между различными соприкасающимися ячейками возможны три ва­рианта: 1) частица компонента, участвующего в обмене на данной фазе перехода, перешла в соседний объем вышележащего подслоя; 2) частица перешла в соседний объем нижележащего подслоя; 3) части­ца осталась в данной ячейке.

Как отмечалось ранее, исключение составляет лишь первый подслой, частицы которого могут об­мениваться с ячейками вышележащего подслоя или оставаться в той же элементарной ячейке, а также подслой, расположенный непосредственно вокруг центра циркуляции (последний подслой). Для ячеек этого подслоя возможны два варианта: 1) остаться в данной ячейке данного подслоя; 2) перейти в со­седнюю ячейку нижележащего подслоя.

Для случая приготовления многокомпонентных смесей эти варианты обмена должны рассчитывать­ся на каждой фазе перехода, причем обмен будет осуществляться лишь с той частью объема элементар­ной ячейки, которая заполнена компонентом, участвующим в обмене на данной фазе перехода.

Пусть коэффициенты вероятности перехода компонентов смеси располагаются в порядке убывания, в соответствии с неравенством Я)13 > Р023 > Р0и.

Рассмотрим все фазы перехода частиц из первого подслоя во второй. В данном переходе участвуют элементарные объемы і и у. В этом случае объем і соприкасается с обечайкой барабана, а объем j распо­лагается непосредственно над ним во втором подслое.

Концентрацию первого компонента в ячейках і и j обозначим через с[1,т^ и, второго компо­нента С2М и фш), концентрация третьего компонента в этих ячейках может быть найдена по зависи­мостям:

фш) = 1 - (фш) + С2М); (4.23)

фш) = 1- (q(j>) + С2и’т)). (4.24)

Однако эти концентрации непосредственно в расчетах представлены не будут.

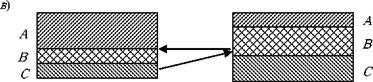
В соответствии с механизмом процесса приготовления многокомпонентной смеси, изображенным на рис. 4.6, компоненту С будет соответствовать номер 1, компоненту В - номер 2, а компоненту А - номер 3.

Первой фазой перехода будем считать переход первого компонента из элементарного объема і в элементарный объем j с последующим вытеснением из последнего третьего компонента.

Вероятность перехода Д 3^7,лз* компонента 1 из ячейки і в ячейку j на данной фазе перехода в мо­мент времени х = ш - Ах равна:

Р^и-ш) = jPOi з (l_ (qO'.-i) + с2и-^1})), (4.25)

где Л); 3 - вероятность перехода компонента 1 в ячейку, содержащую компонент 3; ' - кон­

центрация компонентов 1, 2, соответственно, в ячейке j в момент времени х = {ш— l) • Ах; т= 1, 2,..., к.

л

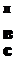
в

с

Рис. 4.6. Мехапизм процесса приготовлепия мпогокомпопептпых смесей

Как видно из этой формулы, вероятность обмена непосредственно зависит от двух параметров: ко­эффициента вероятности перехода первого компонента в ячейку, содержащую третий компонент РОj 3,

и от объема, занятого третьим компонентом в ячейке j’ причем с увеличением этого объема увеличива­ется и вероятность.

Тогда количество компонента 1, содержащегося в ячейке_/ после этой фазы перехода будет равно:

= і) + _ (4.26)

Левая часть суммы представляет собой объем первого компонента, перешедшего из ячейки і в ячейку j. Она равна произведению вероятности обмена д]!'!'",! на концентрацию, а, следовательно, и

объем первого компонента в элементарной ячейке /

Вторая часть суммы представляет собой содержание компонента 1 в ячейке j перед данной фазой обмена.

Как видно из этой зависимости, на данной фазе перехода содержание первого компонента, более склонного к сегрегации, чем третий компонент, в ячейке, лежащей ближе к центру циркуляции, увели­чивается. Это отражает влияние механизма сегрегации на процесс обмена компонентами.

Так как величина объема каждой из элементарных ячеек после любой фазы перехода должна оста­ваться неизменной, количество третьего компонента, перешедшего из ячейки j в ячейку 7, должно стро­го соответствовать количеству первого компонента, перешедшего из ячейки 7 в ячейку J’ т. е. объемы вытесняемого и вытесняющего компонентов равны на любой фазе перехода:

фш) = Ph(4.27)

где Д Э' 7'"''1 ! - объем третьего компонента, вытесненного из элементарной ячейки j первым компо­

нентом.

Рассмотрим вторую фазу перехода. Результатом этой фазы должно быть вытеснение вторым ком­понентом из ячейки 7, третьего компонента, содержащегося в ячейке/ Эта фаза полностью соответству­ет механизму процесса смешивания многокомпонентных смесей, изображенному на рис. 4.6, б.

Зная величину вероятности перехода Р02 3 , можно определить вероятность обмена Р2 б1'",!:

Р2 = Р02 3 + С2и’т-1))), (4.28)

где - содержание первого компонента в ячейке j после первой фазы перехода.

Содержание второго компонента в ячейке j после второй фазы перехода можно определить по зави­симости:

Объем вытесненного третьего компонента равен p2^1,J’ni> ■ С

увеличится:

р Uj. ni) Г2,Ъ

На третьей фазе перехода произойдет вытеснение второго компонента из ячейки j первым компо­нентом из ячейки І.

Вероятность этой фазы обмена определяется зависимостью:

Рі^^) = Р0ІЛС2{^1). (4.31)

Содержание первого и второго компонентов после этой фазы перехода определяется по зависимо­стям:

sib',™) _ р U. J.41) і) 4- ■

Ч - м,2 Ч +Ч j

г О'.т) - р Uj. hi) rU. ni-U, г U. H1-U Ч — - ч, 2 Ч +Ч

Чтобы полностью охарактеризовать состояние системы после последней фазы перехода необходи­мо определить концентрации С^1,т^ и С2и"':

ґ<(і. ііі) _ ^U. m-1) _ p U. J.m) гU. m-U ■ 4 — 4 -4,2 4 5

Q^j. m) = q)j. hi-U _ д Uj. m) qU. iii-Й

В реальных расчетах концентрация на первых двух фазах перехода не рассчитывается, а вместо нее рассчитывается содержание первого компонента, оставшегося в ячейке і после первой фазы перехода:

(jU. m) _ (jU, in-) _ {i. J.m) qU. hi-1

а также содержание второго компонента, оставшегося в ячейке і после второй фазы перехода:

qU.™) _ c^U. m-U _jd U. j.m) £<U, iii-) 0 27)

На практике процесс смешивания не носит ярко выраженного фазового характера, но очевидно, что в механизме сегрегации в первую очередь будут участвовать компоненты, наиболее склонные к ней и лишь затем компоненты, менее склонные к сегрегации.

Допущение о фазовом характере процесса сегрегации при приготовлении многокомпонентных сме­сей не обнаруживает большого расхождения между реальным процессом и результатами расчета по данной модели и, следовательно, имеет законное право на существование.

Из анализа ячеечной модели процесса смешивания следует, что в результате длительного смешива­ния нескольких компонентов, имеющих разную склонность к сегрегации, вокруг центра циркуляции будет расположен компонент, наиболее к ней склонный. Результаты экспериментальных исследований наглядно подтверждают данное утверждение.

Послойпая модель процесса смешивапия. При моделировании процессов сушки, грануляции и классификации полидисперсных материалов во вращающемся гладком барабане необходимо учитывать процессы смешивания и сегрегации этого материала в поперечном сечении барабана, поскольку от рас­пределения частиц, т. е. от их взаимного расположения, во многом зависят интенсивность и эффектив­ность реализуемого процесса.

Ячеечная модель смешивания сыпучего материала, в которой весь материал разбивался на подслои и элементарные объемы, в данном случае может быть значительно упрощена. Как показали результаты экспериментальных исследований, концентрация ключевого компонента (гранул определенного диапа­зона размеров) в поперечном сечении барабанного гранулятора изменяется по подслоям, а в элементар­ных объемах каждого подслоя концентрацию ключевого компонента можно считать одинаковой. Ана­
логичные результаты получены при определении концентрации ключевого компонента (частиц с опре­деленной удельной плотностью) в элементарных объемах и подслоях в поперечном сечении барабанной сушилки. Такая же ситуация складывается в поперечном сечении барабанного смесителя, если в него сначала загрузить основной компонент, а затем во вращающийся барабан, равномерно по его длине, произвести загрузку ключевого компонента. В результате такой операции ключевой компонент равно­мерно распределится в одном или нескольких (в зависимости от соотношения объемов основного и ключевого компонентов) наружных подслоях циркуляционного контура. Учитывая это, достаточно оп­ределить концентрацию ключевого компонента в каждом подслое, чтобы охарактеризовать состояние системы.

Как и в ячеечной модели, принимаем, что циркуляционный контур состоит из ряда подслоев. Пусть первоначальное состояние системы (при х = 0) характеризуется значениями концентрации ключевого компонента в каждом подслое, т. е. известны величины бт(0), 63(0), ... Q(0), ..., CJ0). Нумерацию подслоев от 1 до п и проведем, начиная от обечайки барабана. Будем считать, что в процессе смешивания пере­ход системы из одного состояния в другое происходит скачкообразно. За один переход принимаем та­кое положение системы, при котором подслой, имеющий самый малый объем, совершит один оборот вокруг центра циркуляции - точки С (см. рис. 4.2). Обозначим объем материала, находящегося в под­слое через Vi.

Поскольку рассматривается процесс смешивания компонентов, склонных к сегрегации, принимаем, что за один переход частица ключевого компонента либо останется в том же подслое, либо перейдет в соседний подслой, расположенный ближе к центру циркуляции.

Вероятность этих переходов можно определить по формулам, аналогичным (4.6), (4.7):

^^ = ^•(1-^-1); (4.38)

= (4-39)

где СМт_х - концентрация ключевого компонента в подслое после перехода (т - 1); Р0 - вероятность

перехода частиц ключевого компонента в подслой, находящийся ближе к центру циркуляции, при нуле­вой концентрации в нем ключевого компонента. Численное значение Р0 определяется при идентифика­ции параметров модели эксперименту.

Концентрацию С]к ключевого компонента в 7-м подслое после перехода К можно определить по следующей формуле:

Ci, k=V^ik/V, (4.40)

где Vm i k - объем ключевого компонента в 7-м подслое после перехода.

Объем Vm ik складывается из объема ключевого компонента Vm i lk, оставшегося в 7-м подслое, и объема Кл. і-ид> который перешел из соседнего нижележащего подслоя 7- 1. Эти объемы равны:

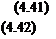Кл, і, і, к~ V q к- Vn с) к_х Pj 1+к к,

К [. /-1. i, k~ V 0-1. к-1 Р-. L к •

Концентрации ключевого компонента в момент времени х = Ах - к можно определить, последовательно используя следующие соотношения:

ДЛЯ /7-го подслоя

Сп, к - Сп, к-1 + Рп-1, п Oj-i, к-1 і (4.43).

для первого подслоя

chk = {chk-1 У-Рлс,к- Vn)/V, (4.44)

для остальных подслоев

С, і = {С, к_, К - Р, м q К + Р,-1.у <7-1, i-i К)/К, (4.45)

где к - номер перехода, к= 1, 2, 3, т.

Число подслоев п, производительность q, границы раздела подслоев R, и их объемы V, найдем, как и для ячеечной модели, т. е. используя формулы (4.8) - (4.15). Время одного перехода в данном случае равно

тЦ R2 - R~) '

Уравнения (4.38) - (4.45) совместно с уравнениями для определения распределения и движения сы­пучего материала во вращающемся барабане представляют собой математическую модель процесса смешивания сыпучих материалов.

Идентификация параметров математической модели сводится к определению по эксперименталь­ным данным наилучшей оценки константы Д.