ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА

КАЧЕСТВЕППЫЙ АПАЛПЗ ПРОЦЕССА СМЕШПВАПИЯ

Процесс смешивания следует рассматривать как сложную физико-механическую систему (ФМС). Стратегия комплексного системного анализа процесса смешивания предполагает на первом этапе каче­ственный анализ ФМС [4]. При этом выделяются два уровня иерархии физико-механических эффектов и явлений, имеющих место при протекании процесса смешивания сыпучих материалов: 1) совокуп­ность физико-механических явлений в локальном объеме (микроуровень); 2) то же в объеме всего ап­парата (макроуровень). Под локальным в данном случае понимается некоторый элементарный объем, в котором содержится достаточно много частиц дисперсных фаз. Структурная схема эффектов первого уровня иерархии ФМС для совмещенного процесса смешивание - измельчение подробно рассмотрена в работе [4], и она может быть использована при анализе процесса смешивания после внесения соответ­ствующих упрощений. Остановимся более подробно на анализе второго уровня иерархии с учетом спе­цифики барабанных смесителей.

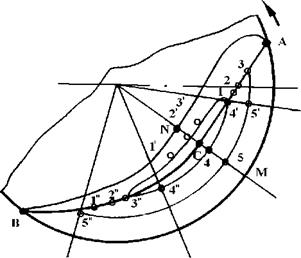
Рассмотрим поперечное сечение вращающегося барабана, частично заполненного сыпучим мате­риалом (рис. 4.1). Можно считать [5], что смешивание материала в поперечном сечении барабана про­исходит за счет перемещения частиц в радиальном и угловом направлениях. Перемещение в радиаль­ном направлении происходит в основном за счет того, что толщина скатывающегося слоя (отрезок CN) меньше толщины поднимающегося слоя (отрезок СМ), и поэтому несколько частиц (1, 2, 3), находя­щихся на разных радиусах в поднимающемся слое, попадают в один скатывающийся подслой (1', 2', 3'). При повторном попадании в поднимающийся слой частицы могут изменить свое взаимное расположе­ние на 1", 2", 3". Очевидно, что чем больше отношение СМ к CN, тем существеннее частица может из­менить свое положение за один оборот вокруг центра циркуляции.

Угловое смещение частиц происходит за счет того, что частицы 4, 5, первоначально находящиеся в одном радиальном сечении поднимающегося слоя, не одновременно переходят в скатывающийся слой (положение 4', 5'), в результате чего после скатывания они попадают в разные радиальные сечения поднимающегося слоя (4", 5"). В скатывающемся слое реализуются одновременно оба механизма сме­шивания, поэтому они могут как усиливать друг друга, так и ослаблять. Кроме этого, при движении в скатывающемся слое частицы соударяются друг о друга и их траектории изменяются. Поскольку со­ударения имеют случайный характер, то и изменения траекторий также случайны. Таким образом, про­цесс смешивания сыпучих материалов в поперечном сечении барабана следует рассматривать как де- терминированно-стохастический.

компоненты, т. е. произойдет сегрегация частиц по размерам или по удельным плотностям материалов, из которых они состоят. Это происходит потому, что при движении в скатывающемся слое мелкие или тяжелые частицы "проваливаются" или "тонут" в зазоры между нижележащими частицами, тем более, что в скатывающемся слое материал разрыхляется, как отмечалось в главе 2. Аналогичная сегрегация происходит в сушилках, где влажные, а следовательно, более тяжелые частицы образуют ядро вокруг центра циркуляции [6]. Таким образом, для более тяжелых и более мелких частиц вероятность перехода в подслой, находящийся ближе к центру циркуляции, будет больше вероятности перехода в подслой, находящийся ближе к обечайке барабана.

Если частицы отличаются только по цвету, то процесс смешивания носит чисто стохастический ха­рактер. Движущая сила процесса отсутствует, так как вероятность перехода из одного подслоя в другой не зависит от концентрации компонентов в этих подслоях. Иначе обстоит дело, когда компоненты от­личаются друг от друга, например, размерами частиц. В этом случае, чем меньше концентрация мелкой фракции в подслоях, находящихся ближе к центру циркуляции, тем больше вероятность перехода мел­ких частиц в эти подслои из подслоев, прилежащих к обечайке барабана. Исходя из этого, целесообраз­но в первую очередь рассматривать процесс сегрегации, поскольку именно ему присуща движущая си­ла процесса, а смешивание компонентов рассматривать как результат сегрегации.

Учитывая, что при качественном анализе структуры процесса смешения, формализуемого как сложная ФМС, выделяются два аспекта: смысловой и математический [4]. В рамках математического аспекта проведем качественный анализ математических подходов, которые могут быть положены в ос­нову описания процесса смешивания сыпучих материалов в барабанных смесителях. Для описания про­цесса смешивания сыпучих материалов наиболее часто используют диффузионную и ячеечную матема­тические модели.

Диффузионная модель [7] соответствует потоку с поршневым движением материала при наличии продольного и поперечного перемешивания частиц. Основное уравнение имеет вид:

dC dC - d С Dr d dC

— = -v------------ Dl—^ +--------------- (R—),

dt dx dx R dR dR

где С — концентрация ключевого компонента; t - время; v - линейная скорость потока; х - координата вдоль потока; Dl и Dr - коэффициенты продольного и поперечного перемешивания (аналоги коэффи­циентов диффузии); R - радиус поперечного сечения потока.

Основной недостаток данного подхода заключается в сложности решения уравнения двухпарамет­рической диффузионной модели и необходимости экспериментального определения значений Dl и Dr на опытных установках.

Сущность второго подхода заключается в том, что процесс смешивания представляется как резуль­тат перераспределения частиц при их движении в потоке материала через систему цепочек, составлен­ных из ячеек идеального смешивания и образующих циркуляционный контур смесителя. Данный под­ход подробно рассмотрен в работе [8]. Используя его, можно составлять уравнения для расчета конеч­ной концентрации циркуляционного контура практически с любым соединением зон, но для многокон­турных схем конечные выражения для концентраций, преобразованных по Лапласу, получаются слож­ными, возникают затруднения обратного их преобразования в оригиналы и расчета истинных значений концентраций.

При построении математического описания на втором уровне иерархической структуры ФМС с учетом закономерностей, имеющих место не в локальном объеме аппарата, а во всем его рабочем про­странстве, наиболее эффективным является математический аппарат случайных марковских процессов [8-10].

Как известно [11], марковские процессы подразделяют на три вида: 1) дискретные в пространстве и во времени; 2) дискретные в пространстве и непрерывные во времени; 3) непрерывные в пространстве и во времени.

Для случая барабанного смесителя, учитывая, что одновременно не весь материал участвует в про­цессе смешивания, а только тот, который находится в данный момент времени в скатывающемся слое, представляется достаточно обоснованным использовать наиболее простой первый вид марковских про­цессов.

Пусть поднимающийся и скатывающийся слои состоят из п подслоев равной объемной производи­тельности, а каждый подслой - из Nj элементарных объемов V(i - номер подслоя, 1 < і < іі). Принима­ем, что за один оборот вокруг центра циркуляции частица может перейти только в близлежащий "верх-

ний" или "нижний" элементарный объем. Именно за счет этих переходов осуществляется перемещение частиц в радиальном направлении. Угловое смещение происходит за счет того, что число элементарных объемов в каждом подслое различно, и слои "проскальзывают" один относительно другого. Следует отметить, что проскальзывание происходит только при скатывании, равно как и переход из одного эле­ментарного объема в другой.

В соответствии с изложенным разделим сынучий материал на подслои и элементарные объемы (рис. 4.2). Нумерацию подслоев начнем от обечайки барабана, а нумерацию элементарных объемов - от линии АС в направлении, противоположном вращению барабана.

Пусть система состоит из к элементарных объемов. Состояние системы после m-го перехода опре­делим вектором состояния Б(т). Координаты вектора есть вероятность нахождения ключевого компо­нента в элементарном объеме после т-го перехода. Вектор можно определить, используя соотношения

Е() = Е(())Р]: Е(2)=Е()Р2:

Е(т)= Е(т-)Рпг

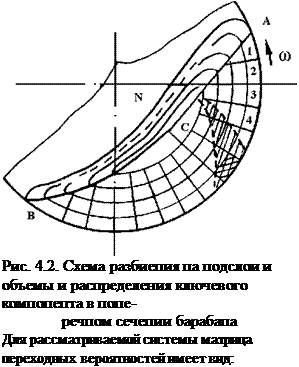где ДО) - вектор начального состояния системы, координаты которого равны вероятностям нахожде­ния ключевого компонента (при т = 0) в 1-м, 2-м и т. д. элементарных объемах; Рт - матрица переход­ных вероятностей, соответствующих /77-му переходу. За один переход будем считать такое положение системы, при котором линию АС пересекут по одному элементарному объему каждого подслоя.

Д Ді Дз ■■■Дк

Ді Дз Дз •••Дк

(4.2)

Ді Дг2 ДгЗ —Ркк

где Рп, P:j - вероятности того, что за один переход частица ключевого компонента останется в 7-м объ­еме и перейдет из 7-го объема в j-й; /и j - номера объемов при единой нумерации.

Для удобства использования матриц введена единая нумерация объемов. В первом подслое нумера­ция идет от 1 до N, во втором - от (TVl + 1) до (TVl + ЛД и т. д. Объем (3 подслоя ос будет иметь номер

Ща ■

Для нахождения матрицы Рт необходимо определить отдельные ее элементы. Если количество подслоев п, то при одном переходе будет происходить обмен частицами ключевого компонента между п элементарными объемами. Возможны три варианта: 1) частица осталась в своем элементарном объе­ме; 2) частица перешла в соседний объем вышележащего подслоя; 3) частица перешла в соседний объ­ем нижележащего подслоя. Исключение составляют первый подслой, для частиц которого возможны только варианты 1-й, 2-й, и последний - варианты 1-й и 3-й.

Таким образом, в матрице Рт{к - п) + (3п - 2) элементов будут отличны от нуля. Из них численное значение (к - п), равное единице, соответствует числу объемов, не участвующих в обмене частицами во время данного перехода. Численные значения (3 п - 2) элементов могут находиться в диапазоне от 0 до 1. Это касается вероятностей Ри, Р1} для объемов, участвующих в обмене частицами ключевого компо­нента при данном переходе. Номера элементарных объемов, участвующих в процессе обмена частица­ми при данном переходе, определяются по выражению

ОС-1

=YuNi +

1= 1

где и* - номер объема подслоя ос, участвующего в процессе смешения при переходе т; Na - количест­во объемов в подслое; выражение "entier" означает, что берется целая часть от числа, находящегося в круглых скобках.

Если частицы не отличаются друг от друга размерами, формой и удельными плотностями, т. е. ком­поненты не склонны к сегрегации, то вероятности перехода частиц ключевого компонента в вышеле­жащие и. нижележащие элементарные объемы равны, т. е.

Р, , = Р,, = Рп ; (4.5)

Ри = -2Рт. (4.6)

Если в качестве ключевого компонента принять частицы меньшего размера, то вероятность пере­хода частиц ключевого компонента в элементарные объемы, находящиеся ближе к обечайке, т. е. при j< і’ равна нулю, а вероятность перехода частиц в объемы, находящиеся ближе к центру циркуляции, т. е. при j > /’ можно определить по следующей формуле:

Рц = РъЪ-С^, (4.7)

где Рт - постоянный коэффициент, который определяется при идентификации параметров математиче­ской модели реальному процессу, равный вероятности перехода частиц ключевого компонента в эле­ментарный объем, находящийся ближе к центру циркуляции при нулевой концентрации в нем ключевого компонента; С} - концентрация ключевого компонента в /-м элементарном объеме после перехода т

- 1.

Когда концентрация ключевого компонента в j-м элементарном объеме равна единице, обмен час­тицами не приводит к изменению концентраций в объемах і и j. Именно поэтому в формулу (4.7) вве­ден сомножитель (l - С t

Механизм процесса смешивания поясним на конкретном примере. Пусть циркуляционный контур состоит из четырех подслоев и количество элементарных объемов в каждом подслое N = 5; N2 = 4; =

3; N2 = 2. Представим циркуляционный контур в развернутом виде (рис. 4.3). Введем единую нумера­цию объемов. Пусть в начальный момент времени, т. е. при т = О, С= С2 = Cj, = 1, а в остальных объе­мах ключевой компонент отсутствует. При т = 1 в зону смешивания перейдут первые объемы каждого подслоя, т. е. при единой нумерации это объемы 1, 6, 10, 13 (рис. 4.3, а). Именно между этими объемами на первом переходе произойдет обмен частицами. Поскольку ключевой компонент находился только в первом объеме, то после первого перехода

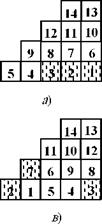
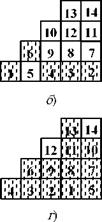
Рис. 4.3. Схема распределепия ключевого компопепта в элемептарпых объемах

частицы ключевого компонента будут присутствовать и в объеме 6 (рис. 4.3, б). При т = 2 в зону сме­шивания выйдут объемы 2, 7, 11, 14 (рис. 4.3, б), и ключевой компонент перейдет в объем 7. Таким об­разом, осуществляется радиальное перемещение частиц, т. е. радиальное смешивание компонентов. На третьем переходе произойдет проскальзывание четвертого подслоя относительно третьего, и объем 13 будет обмениваться частицами с объемом 12, т. е. осуществится угловое перемещение частиц (рис. 4.3, в). На рисунке 4.3, .гпоказано состояние системы на десятом переходе.

Для выяснения механизма осевого смешивания сыпучих материалов разделим барабан по длине на участки с шириной, соизмеримой с размерами смешиваемых частиц. Рассмотрим движение отдельной частицы на /-м участке. При движении в поднимающемся слое частица неподвижна относительно обе­чайки барабана и осевого перемещения, следовательно, и смешивания не происходит. В скатывающем­ся слое частица соударяется с другими частицами, в результате чего траектория ее движения будет не прямолинейной, и она может перейти на соседние участки У - 1 или /'+ 1. За один цикл движения в ска­тывающемся слое частица может переместиться на несколько участков, но может и остаться на перво­начальном участке. В общем случае можно сказать, что чем больше длина пути частицы в скатываю­щемся слое, тем вероятнее большее отклонение частицы от первоначального состояния.

Следует отметить, что осевое смешивание в барабанных смесителях периодического действия осу­ществляется значительно медленнее, чем радиальное. Осевое смешивание играет большую роль для смесителей непрерывного действия, поскольку именно от интенсивности осевого смешивания во мно­гом зависит сглаживающая способность смесителя, а следовательно, требования к дозаторам исходных компонентов и в конечном счете качество готовой смеси.