Особенности движения гранул в грануляционной башне
Характер движения гранул и закономерности их распределения по сечению башни во многом определяют эффективность теплообмена и гранулообразования, время и высоту падения гранул.
Для выбора уравнений движения гранул в башне необходимо прежде всего установить степень стесненности капель (гранул) и режим их обтекания газовым потоком. При средней объемной концентрации частиц менее 0,005—0,01 влияние стесненности на скорость витания не превышает 5% при любом режиме обтекания частиц газовым потоком [114]. Средняя объемная концентрация гранул в грануляционных башнях обычно составляет 0,00002 [ПО], что указывает на пренебрежимо малую вероятность стесненности. Следовательно, для описания характера движения капель (гранул) можно исходить из закономерностей движения одиночной сферической частицы.
Система дифференциальных уравнений движения тела, брошенного под углом к горизонту в неподвижной вязкой среде, и ее решение для условия постоянства коэффициента сопротивления впервые приведена в работах Н. Е. Жуковского.
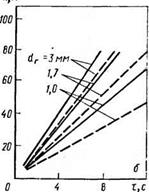
Зависимость дальности вылета
 - падение в неподвижном воздухе; штриховка — при w = 2 м/с):
- падение в неподвижном воздухе; штриховка — при w = 2 м/с):
|
|
С применением этих уравнений для описания закономерностей движения капель (гранул) в башне рассчитана [111] максимальная горизонтальная дальность вылета гранул хтях в зависимости от угла вылета и горизонтальной составляющей начальной скорости движения капель в момент их отрыва (рис. 5.3).
В работе [110] приводится формула для определения высоты падения сферической частицы в случае вертикального ее падения и при условии постоянства коэффициента сопротивления:
//=(— ШтТ — g/т2) — {ft — lg[(l — a exp 2fT)/(l-f-a)]}, (5.12)
где f= (6ctpgfnptdTy/2 a=[(gf^) + wB]f[(glf)—wB]; wT — скорость твердых частиц; wH — скорость воздуха; т — время; С/ — коэффициент аэродинамического сопротивления.
Скорость движения гранул изменяется от w0 = 3—5 м/с [110] до скорости витания nyB, зависящей от размеров и плотности гранул. Для определения wB можно рекомендовать интерполя-
ционную формулу Тодеса [115]:
Re„=Ar/(18+0,61Ar‘/2). (5.13)
Для определения дальности вылета (капель) гранул при использовании центробежных разбрызгивателей предлагается [112] следующая эмпирическая зависимость:
хт«х=0,75ыо— (Тт^т)1/!- (5.14)
Уравнения (5.12) и (5.14) получены для случая движения одиночной частицы в неподвижной вязкой среде (в воздухе).
В грануляционных башнях, как известно, охлаждающий воздух просасывается вентиляторами снизу вверх со скоростью 0,3—0,4 м/с, а в башнях с расположенным внизу кипящим слоем скорость воздуха достигает 1,5—2,0 м/с. Поэтому для более точных расчетов необходимо учитывать тормозящий эффект обтекающей гранулы среды.
Решение задачи движения гранул с учетом переменной относительной скорости гранул и воздуха приведено в работе [ИЗ]. Уравнения движения записаны в виде:
(d2x/dx2) - р аиРотк dx/dx = 0 | (5 151
(d2#/dx2) -f awomn+1 = g j ’
где ow„= [(dx/dx)2-f (d«//dx+ttf)2] »/*; o=pcf/„/2m; /м — мнделево сечение гранулы.
Система уравнений (5.15) решена применительно к статическим разбрызгивателям, для которых характерно истечение струй под сравнительно небольшим углом к вертикальной оси, поэтому авторы пренебрегают горизонтальной составляющей скорости и принимают иДт, = йУверт + йУ. Для инженерных расчетов рекомендованы следующие выражения (при условии С[ = const):
Wot«=Wb{ [exp (2т/тв) — k-lk+]l[exp(2T/xB)+k-lk+]}, (5,16)
Xmax=UoropX,[2/(M:-)l'2]arctg(*-/fc-i-)1/2. (5.17)
где xB=wjg; k±=l±UoiwB-, wB= (g/a),/s.
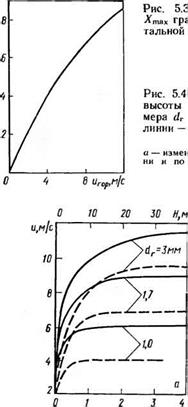
Рассчитаны [ПО] значения скорости и высоты вертикального падения гранул различной величины в зависимости от времени при следующих условиях: и0 = 4 м/с; w = 0 и 2 м/с (рис. 5.4).
Для определения времени падения частиц использовано уравнение Леппла:
Re
х = (2mdT/p/M) f d Re/Cf (Re2B - Re2), (5.18)
Rro
где m — масса гранулы; Re0, Re„ и Re — числа Re, соответствующие Wo, а>в и w за время падения х.
Высота падения гранул была определена методом графического интегрирования: