Гранулирование

Движение материалов при окатывании

Характер движения сыпучего материала во вращающихся аппаратах определяет их транспортную производительность, а также существенно влияет на эффективность процесса гра­нулирования. Кроме того, для обоснованного выбора оптималь­ных технологических параметров процессов гранулирования необходимо знать время пребывания материала в аппаратах различного типа.

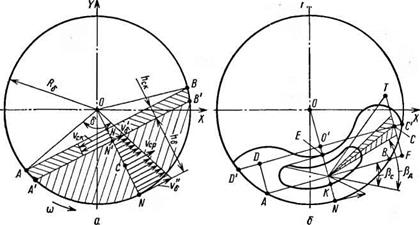
Движение материала в барабанах с гладкими стенками. Известно, что в поперечном сечении гладкого вращающегося барабана сыпучий материал движется по замкнутому циркуля­ционному контуру. Материал, находящийся в грануляторе, можно разделить на поднимающийся (ANB) и скатывающийся (АА'ВВ') слой (рис. 2.3,а). Принято, что первый слой толщи­ной Лб вращается вместе с барабаном и неподвижен относи­тельно его поверхности (цитируется по [55]). Второй слой ма­териала движется по первому в противоположную сторону, толщина его Лск меньше толщины первого слоя, а средняя ско­рость скатывания vCK больше. Между ними находятся частицы, которые вращаются и выполняют роль катков для скатывания подвижного слоя. Измерение толщин подвижного и неподвиж­ного слоев позволяет, по мнению автора, определить среднюю скорость скатывания частиц материала. Сыпучий материал (в сечении — сегмент) поворачивается вместе с барабаном от­носительно оси вращения, поэтому в любой точке сегмента мож­но определить скорость движения частиц — из выражения ои= = ы/?б.

Предположив, что в подвижном слое, в сечении N—N, ско­рость Иск одинакова по всей толщине, а в неподвижном слое

скорость подъема меняеется от г/б до гд/', автор определяет количество материала, скатывающегося в единицу времени через сечение N—N:

QcK = FCK^CKl

и поднимающегося:

Сб = ҐбЄбСР,

где /-ск=Лскіб — площадь поперечного сечения скатывающегося слоя; L6 — длина барабана; Дб=/гв^б — площадь материала, поднимающегося с бара­баном.

Из условия равенства количества поднимающегося и ска­тывающегося материала получена зависимость для определе­ния средней скорости скатывания:

пск=пбср/гб/Аск. (2.51)

Значения Об и оСк замеряют в процессе проведения экспери­мента. На основании полученных экспериментальных данных, автор предлагает определять зависимость среднего времени скатывания частиц материала от средней скорости слоя, вра­щающегося вместе с барабаном. Но при этом указывается, что действительная скорость скатывания частиц по свободной по­верхности больше, а время меньше, чем расчетные, так как слой скатывающихся частиц менее плотный, чем слой частиц, под­нимающихся вместе с барабаном.

Использование предложенных зависимостей требует прове­дения большого объема экспериментальных работ, что ограни­чивает область их применения.

На основе рассмотрения динамики движения материала во вращающихся печах получена система уравнений, описываю­щих кинематику движения частиц в пересыпающемся слое. Однако эту систему уравнений аналитически решить нельзя, по­скольку неизвестен угол рд (рис. 2.3,6), образованный поверх­ностью ссыпающегося слоя с горизонтальной плоскостью и оп­ределяемый экспериментально (цитируется по [55]).

Аналитическое уравнение для расчета рд получено [56] на основании следующих предпосылок: ссыпание материала пред­ставляет собой движение частиц по наклонной плоскости, об­разованной поверхностью откоса слоя. Количество материала, проходящего при вращении барабана через различные сечения по длине верхней половины хорды поднимающегося слоя, про­порционально окружным скоростям соответствующих концен­трических окружностей, т. е. их диаметрам. Поэтому материал поступает через хорду слоем треугольного поперечного сечения с вершиной в ее центре. Рассматривая поперечное сечение под­нимающегося слоя как прямоугольный треугольник КЕТ (см. рис. 2.3,6) с основанием, равным lx. J2, автор определяет поло­жение центра тяжести через усредненные размеры ссыпающего­ся слоя:

tg(P« — Рс)=2/ім. п//х. п=2Л„.п/[Рб2— (Об cos Ф/2+ftVn)]1'2, (2.52)

где Рд — угол, образованный поверхностью ссыпающегося слоя с горизон­тальной поверхностью; fJc — угол ссыпания; h„.n — высота ссыпающегося слоя; D6—диаметр барабана; Ф — центральный угол сегмента, занятого ма­териалом.

Высота ссыпающегося слоя (в м);

лРбп (1 — cos Ф/2) [£>б (1 + cos Ф/2) - f 2/tM п]_________

138,6g®-5 (V „/cos рс)«.б + 2лп [D6 + (1 + cos Ф/2) + 2hM „] '

(2.53)

Средняя скорость движения материала вдоль оси барабана (в м/с);

v _ 4,62g<l-5/i1-bM п [Q26 _ (Рб cos ф/2 + у П)2]°-Б sin ап /2 54. °с D26 (Фл/180 — sin Ф) cos0-5 рс sinp; ‘ ' ' 9

Среднее время пребывания частиц в ссыпающемся слое (за одно осыпание) (с)

Тм.„=2/х. п/3№м.„=2{[£>62(£бсоа ®/2-fftM.„)2]cos pc/3gftM. n}1/2, (2.55)

где Wm. п — средняя скорость ссыпания (в м/с), определяемая по уравнению

U7M. n=te/iM. n/3cospc)“.5. (2.56)

Время пребывания частиц в поднимающемся слое (в с);

т„.п= (60/я£>бП) {D62— {Do cos Ф/2+2йм. п)2+

+16/3 [(Дб/2)(1 - cos Ф/2) —/ім. п]2},/2. (2.57)

Уравнения (2.52) — (2.57) справедливы в случае, когда раз­ница углов (рд—рс) не превышает 6—8°, т. е. при частоте вра­щения барабана 0,5—2,0 С-1. В производстве многих гранули­рованных продуктов она значительно выше, что снижает воз­можный диапазон использования уравнений (2.52)—(2.57) для расчета грануляторов, реакторов и другого оборудования.

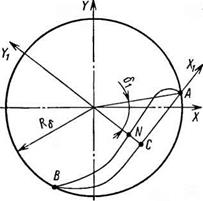Утверждают [57], что если известно уравнение, описываю­щее границу раздела поднимающегося и скатывающегося сло­ев материала (линия АСВ, рис. 2.4), то определение времени пребывания частиц в подни­мающемся слое не представля­ет трудностей. Сложнее опре­делить время пребывания ча­стиц в скатывающемся слое, поскольку при скатывании про­исходят разрыхление и слу­чайные соударения частиц, что влияет на их скорости и траек­тории движения. Скорости, траектории движения частиц, а следовательно, и время их пребывания в скатывающемся

Рис. 2.4. Схема движения сыпучего
материала

слое неодинаковы по толщине этого слоя. Автор [57] предла­гает определять среднее время Тс пребывания частиц в скаты­вающемся слое, т. е. время, за которое произойдет полное об­новление материала этого слоя.

Количество материала, находящегося в скатывающемся слое, при этом равно:

QcK=Q — Qn, (2.58)

где Q= 1/2/.6рн/?і>5(2бо — sin260)—общее количество материала в бараба­не; Qn=FnLepn — количество материала, находящегося в поднимающемся слое.

Площадь Fп поперечного сечения поднимающегося слоя можно определить по следующему выражению [57]:

хв

Ах2 dx — о хи

где А = 2Лб sin 60 sin (б0—6i)/(2RB sin 60 cos(60—6|)— Rc, sin 6i]2;

XB=2/?Bsin60cos(6o —6[) — /?6sin6i; xD=Rc, sin6|.

Среднее время пребывания материала в скатывающемся слое

Tc=2Qc/4pHto (Re2 — Rc2) ■ (2.59)

Как указывает автор [57], в приведенных зависимостях от­сутствуют эмпирические коэффициенты, для определения ко­торых требуются модельные установки.

Движение материала в грануляторах тарельчатого типа. Характер движения гранулируемого материала в тарельчатых грануляторах имеет свои особенности, обусловленные значи­тельной величиной центробежных сил, развивающихся при вра­щении тарелки [59].

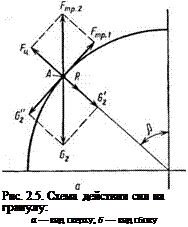
Движение гранул на тарелке определяется системой сил, зависящих, в свою очередь, от скорости вращения и угла на­клона тарелки, ее диаметра, а также от коэффициента трения частиц материала друг о друга. Под действием сил гранулы прижимаются ко дну тарелки, поднимаются на определенную высоту, а затем под действием силы тяжести скатываются вниз. В работе указывается, что до момента отрыва гранулы от борта тарелки все силы уравновешивают друг друга (рис. 2.5) [59]:

G2"=FtpI; R,+G2’=Fn+FTP cos р. (2.60)

Тело отрывается от борта и начинает скатываться по по­верхности тарелки в тот момент, когда сила R (реакция борта) становится равной нулю, т. е. проекция силы тяжести тела G2 уравновешивается суммой центробежной силы и проекции силы трения FTP2 на направление радиуса тарелки ОА

G2,=Tu+TTP2 cos р,

или mgsinacosp=(mo02//?T)+ff4?cosa/cosp, (2-61)

где t>o — линейная скорость вращения, м/с; Rr—радиус тарелки, м; f—ко - эффицвеит треиия материала о поверхность днища тарелки; а — угол накло­на днища тарелки к горизонту, град; р — угол отрыва тела от борта та­релки, град.

После несложных преобразований получено:

ЛіП2/900= (sin а — f cos а) cos (5. (2.62)

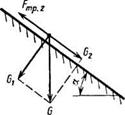
После отрыва от борта частицы материала движутся по до­вольно сложной траектории. Различное положение на плоско­сти тарелки падающих потоков частиц разной крупности неиз­бежно вызывает вполне определенное расположение гранул и по высоте слоя. Первыми к борту тарелки, а следовательно, и на днище поступают самые мелкие фракции, выше распола­гаются более крупные частицы. На самом верху располагаются комки максимального размера. Дальше цикл повторяется: на определенной высоте, соответствующей критическому значению угла р, скатываются самые крупные комки, затем по мере подъема скатываются по тарелке гранулы меньшего размера. По мере увеличения размеров частиц траектория их представит собой своеобразную неправильную спираль, в которой каждый последующий виток располагается в плоскости, отходящей от поверхности диска гранулятора, а нисходящая ветвь витка при­ближается к борту тарелки (рис. 2.6). Анализ уравнения (2.62) показывает, что при оптимальных условиях работы тарельчато­го гранулятора угол наклона тарелки и частота вращения ве­личины взаимосвязанные. При малой скорости вращения та­релки гранулы не достигают верхней точки, при чрезмерно большой — скапливаются около скребка, обнажая центральную часть тарелки. В обоих случаях производительность грануля­тора снижается из-за плохого использования поверхности та­релки.

Рис. 2.6. Траектория движения материа-
ла на тарели гранулятора