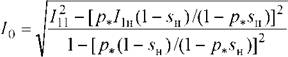Асинхронного двигателя по каталожным данным
Как правило, в каталогах [1] на асинхронные двигатели приводятся следующие технические данные:
Ря - номинальная мощность двигателя, кВт;
С/1н- номинальное фазное напряжение, В;
пя - номинальная частота вращения, об/мин (или лн- номинальное скольжение, о. е.);
г|н — коэффициент полезного действия в режиме номинальной мощности (100%-я нагрузка), %;
cos (р - коэффициент мощности в режиме номинальной мощности, н
кратность пускового момента, о. е.
Эти данные позволяют определить параметры схемы замещения при следующих основных допущениях:
• магнитные и механические потери в двигателе составляют
• активные сопротивления статорной и роторной обмоток полагаются независящими от режима работы двигателя, т. е. эффекты вытеснения не учитываются.
|
|
Определяется ток холостого хода асинхронного двигателя [2]:
где /1н - номинальный ток статора двигателя, A; sH =(п0 -nH)/nQ - номинальное скольжение, о. е.; и0 - синхронная частота вращения, об/мин U 1н - номинальное фазное напряжение, В;
|
|
(5.22)
ток статора двигателя при частичной загрузке, A; coscpp*- коэффициент мощности при частичной загрузке, о. е.; цр* - КПД при частичной загрузке, о. е.; р*=Р/Ря - коэффициент загрузки двигателя, о. е.; Р -
мощность двигателя при частичной загрузке, кВт.
Коэффициенты мощности и КПД при частичной загрузке в технической литературе приводятся редко, а для целого ряда серий электрических машин такие данные в справочной литературе отсутствуют. Эти параметры можно определить, руководствуясь следующими соображениями:
• современные асинхронные двигатели проектируются таким образом, что наибольший КПД достигается при загрузке на 10 ч-15% меньше номинальной [1]. Двигатели рассчитываются так потому, что большинство из них в силу стандартной дискретной шкалы мощностей работают с некоторой недогрузкой. Поэтому КПД при номинальной нагрузке и нагрузке р.., = 0,75 практически равны между собой, т. е.
Лн ~ Ло,75 j
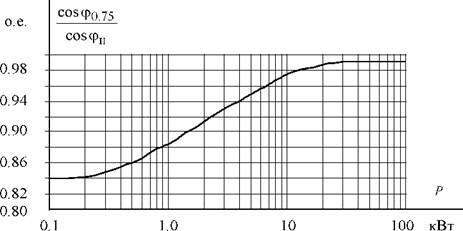
• коэффициент мощности при той же нагрузке р* = 0,75 сильно отличается от коэффициента мощности при номинальной нагрузке, причем это отличие в значительной степени зависит от мощности двигателя и для известных серий асинхронных двигателей с достаточной для практики точностью подчиняется зависимости, приведенной на рис. 5.5.
|
Рис. 5.5. Зависимость coscp0 75/coscpH от мощности асинхронного двигателя |
Значение коэффициента Р согласно источнику [3] находится в диапазоне 0,6 - т - 2,5.
Определим коэффициент [2]
At = т ■ t/,V (1 - sH)/(2 • С, ■ ігшах ■/>„). (5.26)
Тогда активное сопротивление ротора, приведенное к обмотке статора асинхронного двигателя:
й2=/41/(Р + 1/*к)С,,Ом. (5.27)
Активное сопротивление статорной обмотки можно найти по следующему выражению:
R, = С, - R2 - Р, Ом. (5.28)
Определим параметр у, который позволяет найти индуктивное сопротивление короткого замыкания Хкя:
Y = V(!Ak)-P2. (5.29)
Очевидно, что при отрицательном подкоренном выражении (5.29) первоначально принятое значение (3 необходимо изменить.
Тогда индуктивное сопротивление короткого замыкания
XKH=yCl-R2. (5.30)
Для того чтобы выделить из индуктивного сопротивления короткого замыкания Хкя сопротивления рассеяния фаз статора Хан и ротора
і
X, воспользуемся соотношениями [4], которые справедливы для серийных асинхронных двигателей.
Индуктивное сопротивление рассеяния фазы роторной обмотки, приведенное к статорной, может быть рассчитано по уравнению
![]()
|
Индуктивное сопротивление рассеяния фазы статорной обмотки может быть определено по следующему выражению: |
|
|
Согласно векторной диаграмме (см. рис. 5.3), ЭДС ветви намагничивания Ет, наведенная потоком воздушного зазора в обмотке статора в номинальном режиме, равна
|
|
|
^1н-cos Фін Яг/ін) (^Лн ' cos ф: + Хіон-/ін) s(5.33) |
тогда индуктивное сопротивление контура намагничивания
|
(5.34) |
— Етн / /Q.
Приведенная методика дает удовлетворительное схождение расчетных механических характеристик и механических характеристик, построенных по трем паспортным точкам на рабочем участке механической характеристике, то есть при изменении скольжения s от 0 до, чк.
Пример 5.2. . Для короткозамкнутого асинхронного двигателя типа 4А112МВ6УЗ определить параметры Т-образной схемы замещения. Двигатель имеет следующие технические данные [1]:
• номинальная мощность Ря = 4 кВт;
• номинальное фазное напряжение UlH = 220 В;
• синхронная частота вращения п0 =1000 об/мин;
• номинальное скольжение £н =0,051 о. е.;
• коэффициент полезного действия в режиме номинальной мощности (100 %-я нагрузка) г|н = 82 %;
• коэффициент мощности в режиме номинальной мощности coscpH =0,81 о. е.;
• кратность пускового тока 1и/11н =kt=6 о. е.;
• кратность пускового момента Мп/Мн =ки=2 о. е.;
• кратность максимального момента Мтах/Мя = ктах = 2,2 о. е.;
• кратность минимального момента Мтт/Мя = ктт = 1,6 о. е.,
Решение. Ток холостого хода асинхронного двигателя
|
|
В табл. 5.1 приведены параметры схемы замещения асинхронного двигателя, рассчитанные по каталожным данным (строка 1), заложенные в проектные расчеты этого двигателя [4] (строка 2), а также погрешность 5 % определения каждого из параметров (строка 3).
Таблица 5.1
|
Параметр |
*1 |
r2 |
у т |
||
|
Расчет |
1,878 |
2,248 |
1,393 |
2,994 |
54,47 |
|
Проект |
1,856 |
1,759 |
1,494 |
2,651 |
48,2 |
|
Погрешность, % |
1Д7 |
21,7 |
8,0 |
11,4 |
11,2 |
Как следует из анализа результатов, приведенных в табл. 5.1, сходимость расчетных параметров схемы замещения и проектных данных завода-изготовителя в основном находится в инженерных допусках.
|
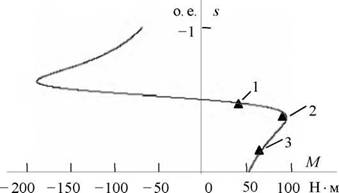
Рис. 5.6. Естественная механическая характеристика асинхронного двигателя: 1 - момент номинальный, 2 - момент максимальный, 3 - момент минимальный |
• Номинальный момент двигателя
Р„ 4000 тт
Мн = —S - =------- = 40,25 Н • м.
н юн 99,36
• Максимальный момент двигателя
Мтах = ^тах - М н = 2,2 • 40,25 = 88,55 Н • М.
• Минимальный момент двигателя
Мшш = ктт • Мн = 1,6 • 40,25 = 64,4 Н • м.
Найденные координаты точек с номинальным, максимальным и минимальным моментом нанесены на рассчитанный график (см. рис. 5.6) естественной механической характеристики асинхронного двигателя в виде треугольников.
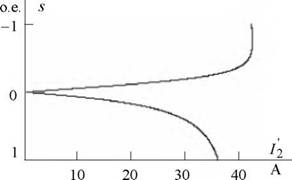
График электромеханической характеристики I2=f(s), рассчитанный по формуле (5.2) в математической системе MathCAD, приведен нарис. 5.7.
|
Рис. 5.7. График электромеханической характеристики Г = f(s) |
|
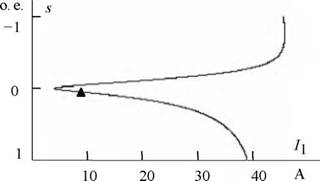
Электромеханическая характеристика Ix= /(л) приведена на рис. 5.8.
Рис. 5.8. График естественной электромеханической характеристики I] = / (л ) асинхронного двигателя: А - точка с номинальными параметрами двигателя |
Динамическая механическая характеристика асинхронного двигателя
В системе уравнений (5.35) приняты следующие обозначения:
Ula - составляющая вектора напряжения обмотки статора, ориентированная вдоль оси а неподвижной системы координат;
Ulb- составляющая вектора напряжения обмотки статора, ориентированная вдоль оси b неподвижной системы координат;
- эквивалентное индуктивное сопротивление об-
мотки статора, равное индуктивному сопротивлению рассеяния обмотки статора и индуктивному сопротивлению от главного поля;
Х2= X+ Хт - эквивалентное индуктивное сопротивление обмотки ротора, приведенное к обмотке статора, равное индуктивному сопротивлению рассеяния обмотки ротора и индуктивному сопротивлению от главного поля;
Хт - индуктивное сопротивление от главного поля (контура намагничивания), создаваемое суммарным действием токов статора;
|fla - составляющая вектора потокосцепления обмотки статора, ориентированная вдоль оси а неподвижной системы координат;
|flb - составляющая вектора потокосцепления обмотки статора, ориентированная вдоль оси Ъ неподвижной системы координат;
|/2а - составляющая вектора потокосцепления обмотки ротора, ориентированная вдоль оси а неподвижной системы координат;
|>2ь ~ составляющая вектора потокосцепления обмотки ротора, ориентированная вдоль оси Ъ неподвижной системы координат;
i2a - составляющая вектора тока обмотки ротора, ориентированная вдоль оси а неподвижной системы координат;
ilh - составляющая вектора тока обмотки ротора, ориентированная вдоль оси Ъ неподвижной системы координат.
Электромеханические процессы в асинхронном электроприводе описываются уравнением движения. Для случая,/v = const
M-MC=JL(5.36) at
где Мс - приведенный к валу двигателя момент сопротивления нагрузки; - приведенный к валу двигателя суммарный момент инерции электропривода.
Анализ динамических процессов преобразования энергии в асинхронном двигателе представляет собой сложную задачу в связи с существенной нелинейностью уравнений, описывающих асинхронный двигатель, обусловленной произведением переменных. Поэтому исследование динамических характеристик асинхронного двигателя целесообразно вести с применением средств вычислительной техники.
Совместное решение системы уравнений (5.62) и (5.63) в программной среде MathCAD позволяет рассчитать графики переходных процессов скорости со и момента М при численных значениях параметров схемы замещения асинхронного двигателя, определенных в примере 5.3.
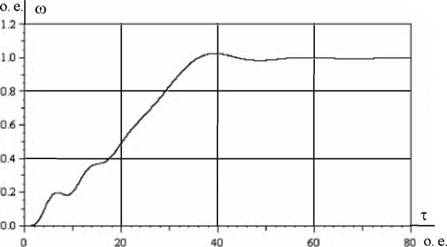
Так как динамическую механическую характеристику асинхронного двигателя можно получить только по результатам расчетов переходных процессов, то вначале приведем графики переходных процессов скорости (рис. 5.9) и момента (рис. 5.10) при пуске асинхронного двигателя прямым включением в сеть.
|
Рис. 5.9. Переходный процесс скорости при пуске короткозамкнутого асинхронного двигателя прямым включением в сеть при моделировании в неподвижной системе координат |
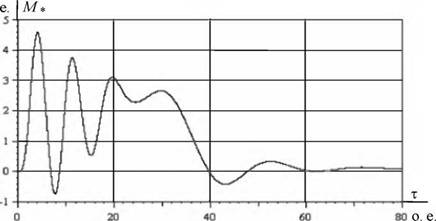
|
Рис. 5.10. Переходный процесс электромагнитного момента при пуске короткозамкнутого асинхронного двигателя прямым включением в сеть при моделировании в неподвижной системе координат |
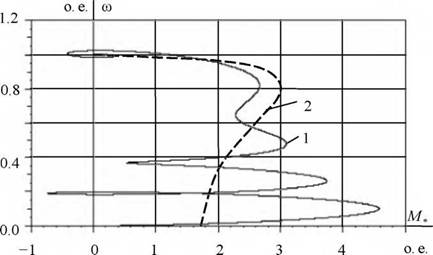
Графики со = /(т) и М = /(т) переходных процессов позволяют построить динамическую механическую характеристику асинхронного двигателя (рис. 5.11, кривая 1) при пуске прямым включением в сеть. Для сравнения на этом же рисунке приведена статическая механическая характеристика - 2, рассчитанная по выражению (5.7) для тех же параметров схемы замещения асинхронного двигателя.
|
Рис. 5.11. Механические характеристики короткозамкнутого асинхронного двигателя: 1 - динамическая; 2 - статическая |
Анализ динамической механической характеристики асинхронного двигателя показывает, что максимальные ударные моменты при пуске превышают номинальный момент Мн статической механической характеристики более чем в 4,5 раза и могут достичь недопустимо боль - тттих по механической прочности значений. Ударные моменты при пуске, и особенно при реверсе асинхронного двигателя, приводят к выходу из строя кинематики производственных механизмов и самого асинхронного двигателя.
Моделирование в программной среде MathCAD позволяет достаточно просто провести исследования динамических механических характеристик асинхронного двигателя. Установлено, что динамическая характеристика определяется не только параметрами схемы замещения асинхронного двигателя, но и параметрами электропривода, такими, как эквивалентный момент инерции J2, момент сопротивления Мс на валу двигателя. Следовательно, асинхронный двигатель при данных параметрах питающей сети и схемы замещения обладает одной статической и множеством динамических механических характеристик.
Как следует из анализа динамических характеристик рис. 5.9-5.10, переходный процесс пуска короткозамкнутого асинхронного двигателя может иметь колебательный характер не только на начальном, но и на конечном участке, причем скорость двигателя превышает синхронную со о • На практике колебания угловой скорости и момента двигателя на конечном участке переходного процесса наблюдаются не всегда. Кроме того, имеется большое число производственных механизмов, для которых такие колебания необходимо исключить. Характерный пример - механизмы лебедок и перемещения подъемных кранов. Для таких механизмов выпускаются асинхронные двигатели с мягкими механическими характеристиками или с повышенным скольжением. Установлено, чем мягче рабочий участок механической характеристики асинхронного двигателя и чем больше эквивалентный момент инерции электропривода, тем меньше амплитуда колебаний при выходе на установившуюся скорость и тем быстрее они затухают.
Исследования динамических механических характеристик имеют теоретическое и практическое значение, поскольку, как было показано в разделе 5.1.1, учет только статических механических характеристик может привести к не совсем корректным выводам и к искажению характера динамических нагрузок при пусках асинхронных двигателей. Исследования показывают, что максимальные значения динамического момента могут превышать номинальный момент двигателя при пуске прямым включением в сеть в 2 - 5 раз и в 4 - 10 раз при реверсировании двигателя, что необходимо учитывать при разработке и изготовлении электроприводов.