Асинхронные электроприводы с векторным управлением

Алгоритмы управления напряжением

Для определения амплитуды напряжения статора двигателя можно записать уравнение

+№■/*)*•

Если Wsm = const, то <P¥sm/dt = 0 и уравнение равновесия Э. Д.С. статора будет Usm = l(здесь принято IsRstt 0). Измерив составляющие вектора потокосцепления статора по осям (а, р) с помощью датчиков э. д. с. (измерительных катушек) и интеграторов, можем определить модуль вектора потокосцепле­ния и частоту его вращения = (Ч^Ч^ — Ч^Ч^)/^, а так­же можно организовать канал управления потокосцепления ста­тора по каналу управления напряжением преобразователя ча­стоты.

Экспериментально были проверены следующие законы управ­ления по каналу напряжения:

*</»)«•. (П.-*«■,)*. usm = k(p)(VL-%s^sm)> -* (РКП,-*«.)•

В схеме, работающей по алгоритму (4.17), максимальный провал при набросе номинальной нагрузки 5—10 %, восстанов­ление — без перерегулирования, длительность переходного про­цесса 0,1—0,2 с. Максимальная статическая погрешность по скорости 3,5 %. Скачкообразное изменение W^m, равное 30 % ба­зового *, отрабатывается за 0,1 с.

В схеме, работающей по алгоритму (4.18), улучшаются по­казатели процессов при пуске и скачке задания угловой скоро­сти. Однако по динамическим характеристикам процессов на- броса и сброса нагрузки и отработки скачка задания потока эта схема уступает предыдущей. При использовании в системе ПИ - регулятора максимальный провал Wsm при набросе номинальной нагрузки составил 35—50 %. Статическая погрешность по Ч^т отсутствует. Отработка скачков задания потока происходит по апериодическому закону за 0,2 с.

В системе, построенной по алгоритму (4.19) с ПИ-регулято - ром, получена максимальная статическая погрешность по скоро­сти 2,5 %, по потоку она отсутствует. Скачкообразные изменения отрабатываются не хуже, чем в рассмотренных выше схемах.

1 За базовый принят поток статора АД, устанавливающийся в разомкну­той системе в номинальном режиме (на выходе вычислителя 4 В).

Для выявления алгоритма управления частотой необходимо оценить поведение функций И (О-фг в переходных режимах.

Примем за базовые величины шо и То, тогда получим сле­дующие уравнения:

6 Т = Л (v> vus) У+ U’, 4r = Im (фЖ) ~ ^ (4,20)

тг kr¥%

где 8 — — , - ; Т = 0е~‘ = (£>0/.

2 ILS0>1

Простейшее асимптотическое приближение можно получить, полагая е -► 0:

0 = A (v, vUs) Т + £/; = Im (ф5фг) — цс. (4.21)

Для предварительно возбужденного двигателя уравнения по каналам напряжения и угловой скорости можно записать в виде:

t/ = C/0 + F1(v£/sl? im); С/0 = ( 1-*Л)К; ^ = F2(va, v),

где Vo — задаваемый закон изменения угловой скорости ротора. Будем полагать, что ve(0) = 0; ^,(0, 1)=»0; Р2(0, 0)==0;

dFі (0, ф5т) __ А. dFi (0, 1) .

*Рш ~ dvus

Для интегрирования системы (4.21) воспользуемся асимпто­тическим методом, развитым А. Н. Тихоновым и А. Б. Ва­сильевой.

Положим

¥ = ¥(8) + 1ГР(т); v = v (9) + IIv (т), (4.22)

где IFF (т) и Ш (г) — граничные функции. Тогда A(v, Us) = Д (0) ТЇА (т);

vUs = (9) - f nv (т);

Фsm ~ Фsm (®) "f" Пфі/п Wl

£/ = £/(0) + nt/(T).

Разделяя члены, зависящие от 0 и т, получаем две системы:

= + Ж = 1т(ФХ)-^. (4.23)

~~ = ПЛ¥ + ЛІТР + ПА ПТ + ПС/;

=е im (пф5ф; + ф5Пф*г + Пф5пф;).

Начальные условия

Т(0) + ПТ(0) = Т0; v (0) + nv (0) = 0.

Из соотношений (4.24) следует, что ITv = 0, a ITvt/s и ПА — величины порядка е.

В соответствии с этими оценками решение систем (4.23) и (4.24) ищем в виде ряда:

ЧГ = Ч'° + еЧ?1+ ПЧ' = П°¥ + еП1Ч'+ ...

Системы (4.23) и (4.24) позволяют определить изменения потокосцеплений в переходных режимах, а также частрты вра­щения векторов потокосцеплений как функций времени:

= 8lm? T^-' <*■*>

(4.26)

где vs — частота вращения вектора потокосцепления статора от­носительно вектора напряжения статора; vr — частота вращения вектора потокосцепления ротора относительно вектора напряже­ния статора.

Угол между векторами потокосцепления статора и ротора

= $Y rsdQ. (4.27)

Угол между векторами потокосцепления и напряжения ста­тора

е

а, = J vs dQ. (4.28)

о

Если в закон управления частотой вращения ввести сигнал, пропорциональный v$, то в процессе увеличения скорости будет осуществляться коррекция частоты напряжения, так чтобы ис­ключались колебания вектора потокосцепления статора относи­тельно вектора напряжения. Таким образом, система регулиро­вания будет ориентировать вектор потокосцепления статора от­носительно вектора напряжения, причем снижается амплитуда колебаний переменной аь и, соответственно, увеличивается раз­виваемый электромагнитный момент.

Следовательно, для канала управления частотой напряжения можно рекомендовать следующий закон:

Vys = v° + £, (р) (v° — v) + k2 (p) vs. (4.29)

На рис. 4.5 показаны расчетные графики изменения а* и при пуске асинхронного двигателя в системе ТПЧ-АД, со стаби­лизацией потокосцепления статора, при управлении по каналу частоты по закону (4.29) при k — 1,5, a k2 в одном случае равен нулю, в другом — единице. Потокосцепление статора в переход­ном режиме поддерживалось с точностью до 1 %.

4,Б. Фазовые соотношения при пуске асинхронного двигателя в системе ТПЧ-АД прй разных законах управления каналом частоты

Из этих графиков видно, что введение сигнала v* позволяет существенно влиять на характер изменения фазовых соотноше­ний в переходных режимах.

В процессе пуска выделяется этап нарастания угла у*, необ­ходимого для того, чтобы обеспечить требуемый электромагнит­ный момент, при этом ротор практически неподвижен. Затем, когда сформировался угол ys, начинается разгон.

4.4. Регулируемый асинхронный привод с управлением по потокосцеплению статора

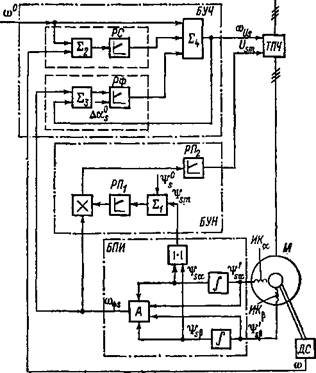
Используя алгоритмы управления по каналам напряжения и частоты ТПЧ можно организовать систему управления асинхрон­ным приводом, в которой задается уровень потокосцепления ста­тора (рис. 4.6).

Блок подготовки информации БПИ содержит датчики э. д. с., интеграторы, вычислители модуля и частоты вращения вектора потокосцепления.

Блок управления напряжением БУН содержит звено сравне­ния задания модуля потокосцепления статора и фактического его значения, регулятор и блок умножения, с помощью которого задание по потокосцеплению преобразуется в задание по напря­жению.

Блок управления частотой БУЧ содержит канал управления частотой и канал управления фазой. Канал управления частотой состоит из сумматора и регулятора частоты. Сигнал по заданию частоты вращения сравнивается с сигналом датчика угловой ско­рости. Сигнал ошибки по угловой скорости привода через

регулятор частоты подается на четвертый сумматор. Канал уп­равления фазой содержит третий сумматор и регулятор фазы. На третьем сумматоре сравниваются сигналы, пропорциональные частоте напряжения и частоте вращения вектора потокосцепле­ния статора. Это позволяет корректировать частоту вращения вектора напряжения, ориентируя его в соответствии с заданием. Таким образом, канал управления напряжением решает задачу управления модулем потокосцепления статора, а канал управле­ния частотой управляет угловой скоростью ротора и фазой век­тора напряжения относительно вектора потокосцепления статора в переходных режимах. При стабильном потокосцеплении стато­ра механические характеристики достаточно жесткие и поэтому угловая скорость ротора может задаваться частотой напряжения статора, вследствие чего этот канал может обеспечить доста­точно точную работу и без обратной связи по угловой скорости ротора, т. е. без датчика угловой скорости ротора.

Для проверки разработанных теоретических положений было проведено исследование на ЭВМ системы управления асинхрон­ной машиной. Для параметров двигателя (55 кВт, 178 Н*м) рас­четы были выполнены при управлении напряжением и частотой по законам;

(4.30)

(4.31)

где kv, km — коэффициенты регуляторов системы управления.

Для проверки устойчивости работы системы привода в про­цессе пуска вводились два типа возмущений: по потокосцеплению статора

-1 + 0,2 [1 - exp(-o. U)];

по моменту нагрузки.

При t = 0,5 с производился наброс момента нагрузки Мс = *= 150 Н-м (|1с — 0,00375), а при t — 1 с — дополнительный на­брос нагрузки Ліс = 50 Н-м (ц* == 0,00125).

Частота напряжения статора АД (тахограмма привода) за­давалась по следующему 8а кону:

—V*.

*Ьв ~ Vi» *є (V *2)»

1 є (U 'з);

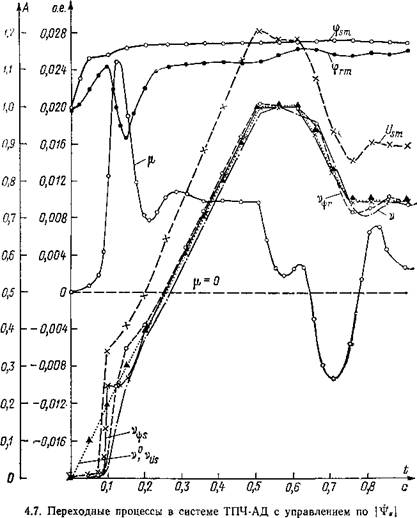
На рис. 4.7 приведены результаты исследований системы управления при fcy = 50 и fe«, = 0. Как видно из приведенных результатов, система работает устойчиво и достаточно точно от­рабатывает задание даже при таком простейшем алгоритме управления. Увеличение ka повышает точность,

Из построенных графиков видно, что на начальном интервале времени t є (0; 0,07) с электромагнитный момент практически равен нулю, несмотря на то, что потокосцепления имеют номи­нальные значения. На низких частотах сказывается мягкость характеристик, критическое скольжение велико и этим можно объяснить малое значение электромагнитного момента. При t = 0,75 с начинается резкий подъем v$s и соответственно рез­кое увеличение электромагнитного момента. Очевидно, что для усиления действия управления целесообразно частоты vus и v$s задавать не с нуля, а с v^s = 0,1, что соответствует полученным соотношениям.

Уравнение по каналу частоты должно быть подчинено техно­логическим требованиям либо задаче минимизации потерь в дви­гателе. Рассмотрим задачу минимизации потерь в обмотках двигателя в процессе пуска в системе ТПЧ-АД. Такая поста­новка задачи представляет интерес для приводов с большими массами. Определим управление следующими законами:

V = ^o+Pv№(l-4>.«); v№ = v°-*(v°-v). (4.32)

Для квадратов модулей токов можем записать

«-■£• (4-зз)

Потери в обмотках за время пуска определяются системой уравнений:

(4-34а)

где It и /г — функционалы, определяющие потери в обмотках ротора и статора.

При задании линейного закона нарастания угловой скорости двигателя при пуске время пуска привода определяется соотно­шением (4.34в).

Пусть задание пуска носит линейный характер. Введем сле­дующие обозначения:

0

° = TrVA’ т' = xr(k + !) 07! vA = VUs — V.

Тогда с учетом выражения (4.21) система, определяющая потери, может быть записана в форме:

/-/, + /,; /,«601*. J (4-35а>

о

Ir = ® ik, r+^dnC'’ (4-356>

0

Іг=1-*АтТ5тф;.' (4-35в)

Функционалы (4.35а) и (4.356) можно привести к одинако' вой форме, если учесть, что

S

о

Обозначим ф^Д.0, = 2*. При 0 = 0! =^т'(& + 1). Тогда мини­мизируемый функционал

/о = тг[(^+ *)(*—!"(*+ У*2— !))]-► min. (4.37)

При а = 1 функционал /о не имеет экстремальной точки; при а < 1 экстремум для /о имеет место при

*m = (2 — а)/(2 VI — а)*

где а < 1.

Можно сделать следующие выводы: при пуске двигателя по­тери в роторе тем меньше, чем больше время пуска; для потерь в м^ди статора существует такое время, при котором эти потери минимальны. При минимизации потерь в обмотках рассмотрим функционал

и

о

Принимая во внимание (4.37) находим, что оптимальное вре­мя пуска привода будет

2 — а, + k2r

где со° — заданная предельная угловая скорость.

Отметим, что минимальное время разгона двигателя в систе­ме ПЧ-АД при стабилизации потокосцепления статора

tm=2tfL's/(mzkskr4*m),

Полученные соотношения могут быть использованы для за­дания таких параметров специальных двигателей, которые обес­печивают двигателю минимальные потери либо минимальное время разгона.