СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Связь между переходной характеристикой и положением корней на s-плоскости
Переходную характеристику замкнутой системы управления можно связать с положением полюсов ее передаточной функции. В общем случае передаточная функция замкнутой системы имеет вид:
|
R(s) A(s) ’ |
где A(.v) = 0 есть характеристическое уравнение системы.
|
|
Для одноконтурной системы, изображенной на рис. 5.14, характеристическое уравнение записывается в виде 1+ G(s) = 0. Переходная характеристика, вообще говоря, определяется полюсами и нулями Ts). Но для замкнутой системы полюсами 7s) являются корни характеристического уравнения Д(л) = 0 и полюсы выражения Р, А> (s) При единичном ступенчатом воздействии и отсутствии кратных корней (если коэффициент усиления системы равен 1) изображение по Лапласу выходного сигнала можно представить в виде разложения на дроби:
(5.21)
где А„ Вк и Ск — константы. Корни системы должны быть либо вещественными, вида s = —cjj, либо образовывать комплексно-сопряженные пары типа s = - ак± jak. Тогда обратное преобразование Лапласа для (5.21) дает переходную характеристику системы в виде суммы членов:
|
|
|
N |
|
м |
|
до
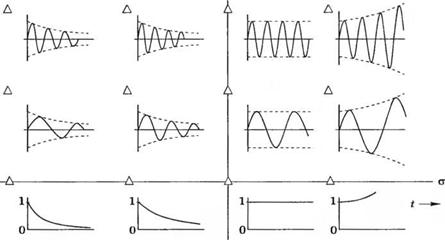
Рис. 5.17. Реакция системы на импульсное воздействие при различном положении корней на s-плоскости (комплексно-сопряженные корни не показаны) |
где константа Dk выражается через Вк, Ск, а* и со*. Переходная характеристика образована установившимся значением y(t), экспоненциальными членами и затухающими синусоидальными компонентами. Чтобы переходная характеристика была ограниченной (а система соответственно, устойчивой), необходимо, чтобы вещественные части корней, - Сj и
-ак, были расположены в левой половине s-плоскости. На рис. 5.17 изображены реакции системы на импульсное воздействие, соответствующие различному положению корней на s-плоскости. Такое наглядное графическое представление очень полезно при выборе желаемого расположения корней на s-плоскости.
При анализе линейной системы управления важно понимать связь между ее представлением в области комплексной частоты в виде полюсов и нулей передаточной функции и поведением системы во времени в виде реакции на ступенчатое и иные входные воздействия. Например, многие вычислительные методы анализа и синтеза в таких прикладных задачах, как управление и обработка сигналов, применяются именно на основе представления модели системы в виде полюсов и нулей передаточной функции T(s). С другой стороны, качество системы часто оценивается по ее переходной характеристике, в особенности когда речь идет о системах управления.
Опытный проектировщик должен ясно представлять, как повлияет на временные характеристики системы добавление, удаление или перемещение на s-плоскости полюсов и нулей T(s). Он также должен понимать, как следует изменить полюсы и нули T(s), чтобы добиться желаемого вида временных характеристик.
Опытный проектировщик всегда представляет, как влияют нули передаточной функции на реакцию системы. Полюсы T(s) определяют отдельные составляющие переходной характеристики, а нули 7T(s) определяют относительный вес каждой из этих составляющих. Например, чем ближе нуль передаточной функции расположен к какому-то ее полюсу, тем меньше вклад в переходную характеристику составляющей, соответствующей данному полюсу.
Можно написать компьютерную программу и задать в ней произвольный набор полюсов и нулей передаточной функции линейной системы. Затем компьютер рассчитает и
построит графики реакции системы на импульсное и ступенчатое воздействия. Кроме этого можно изобразить те же характеристики в уменьшенном масштабе вместе с диаграммой размещения полюсов и нулей. После того, как программа будет выполнена для исходного набора полюсов и нулей, пользователь может изменить положение одного или нескольких из них. В результате будет получена диаграмма, отражающая старое и новое расположение полюсов и нулей и старые и новые реакции системы на импульсное и ступенчатое воздействия.