СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Переменные состояния динамической системы
Анализ и синтез систем управления во временной области основан на понятии состояния системы. Состояние системы—это совокупность таких переменных, знание которых, наряду со входными функциями и уравнениями, описывающими динамику системы, позволяет определить ее будущее состояние и выходную переменную. Для динамической системы ее состояние описывается набором переменных состояния [ЛГ[(?), X2(t) Х„(0]- Это такие переменные, которые определяют будущее поведение системы, если известно ее текущее состояние и все внешние воздействия. Рассмотрим систему, изображенную на рис. 3.1, где^,^) иy2(t) есть выходные переменные, a ux(t) и u2(t)— входные переменные. Для ЭТОЙ системы переменные (*[, х2,..., хп) имеют следующий смысл: если в момент времени t0 известны начальные значения [^(fo), x2(t0), ...,xn(tQ)] и входные сигналы щ(і) и u2(f) для t > t0, то этой информации достаточно, чтобы определить будущие значения всех переменных состояния и выходных переменных.
|
Входные сигналы |
|
Выходные сигналы я ш 14(f) |
|
н(*) Ц,(і) |
|
Система |
|
Рис. 3.1 Структурная схема системы управления |
Переменные состояния описывают поведение системы в будущем, если известны текущее состояние, внешние воздействия и уравнения динамики системы.
Общий вид динамической системы приведен на рис. 3.2.
Простым примером переменной состояния может служить положение выключателя электролампочки. Выключатель может быть в одном из двух положений — «включено» или «выключено», поэтому его состоянию соответствует одно из двух возможных значений. Если мы знаем, в каком состоянии (положении) находится выключатель в момент времени t0, и если мы прикладываем к нему воздействие, то мы всегда можем определить будущее состояние элемента.
|
Рис. 3.2 Динамическая система |
|
*(0) Начальные условия |
|
u(t) Вход |
|
Состояние системы x(t) |
|
y(t) Выход |
|
-ї>: |
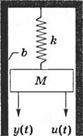
Понятие о переменных состояния, описывающих динамическую систему, можно проиллюстрировать на примере механической системы «масса-пружина» с затуханием, изображенной на рис. 3.3. Число переменных состояния, выбираемых для описания системы, должно быть по возможности минимальным, чтобы среди них не было излишних. Для данной системы вполне достаточно иметь две переменные состояния — положение и скорость движения массы. Таким образом, мы примем В качестве переменных СОСТОЯНИЯ совокупность (Х[, х2), где
|
|
|
Трение о стенки |
|
Рис. 3.3. Система «масса-пружина» с затуханием |
dy(t)
xx(t)=y(i) И x2(t) = -
dt
Дифференциальное уравнение, описывающее поведение системы, обычно записывается в виде
|
d2y |
|
(3.1) |
|
М |
|
+ b^- + ky = u(t dt2 dt |
С учетом введенных выше переменных состояния это уравнение примет вид:
|
. dx 2 |
|
+ bx7 + кх | —и (/) |
|
(3.2) |
|
М- |
|
Следовательно, исходное дифференциальное уравнение второго порядка мы можем представить в виде эквивалентной системы двух дифференциальных уравнений первого порядка: dxx ~dt |
|
(3.3) (3.4) |
|
= х |
|
2 ■ |
|
dx2 dt |
|
к Ь Х, X, М М ' |
|
1 н и. М |
|
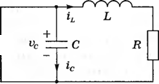
Эти уравнения по сути описывают поведение системы в терминах скорости изменения каждой переменной состояния. Другим примером системы, которую можно описать переменными состояния, является ТЛС-цепь, изображенная на рис. 3.4. Состояние системы характеризуется двумя переменными (Х[, х2) где хх есть напряжение на конденсаторе vc(/), и х2 — ток через индуктивность //(/). Выбор этих переменных интуитивно понятен, т. к. общая энергия, запасенная в цепи, непосредственно зависит от них, как E=(l/2)Z,/£ +(1/2)Cvc2. (3.5) Таким образом, Х](/0) и x2(t0) несут информацию о полной начальной энергии в цепи и, следовательно, о состоянии системы в момент t = /0. Для описания пассивной ЛіС-цепи число необходимых переменных состояния равно числу независимых элементов, накапливающих энергию. Используя закон Кирхгофа для токов, запишем дифференциальное уравнение первого порядка, определяющее скорость изменения напряжения на конденсаторе: іс ~С - у - = u(t)~ і і • (3.6) at |
|
u(t) Источник4^ тока |
|
Рис. 3.4. RLC-цепь |
|
|
Закон Кирхгофа для напряжений, примененный к правому контуру, дает уравнение, определяющее скорость изменения тока через индуктивность:
L^=-Ri, + vc. (3.7)
dt 1
Выход системы определяется линейным алгебраическим уравнением:
v0 = RiL (О-
Уравнения (3.6) и (3.7) мы можем переписать в виде системы двух дифференциальных уравнений относительно переменных состояния хх и х2:
(3.8)
*L-lx --Х Г3 9Ї
dt ~~L l L (39)
Тогда выходной сигнал будет равен
^i(0 = v0(0 = R х2. (3.10)
Используя уравнения (3.8) и (3.9), а также начальные условия [x,(f0), х2(/0)], мы сможем определить будущее поведение системы и ее выходную переменную.
Переменные состояния, описывающие систему, не являются единственными, и всегда можно выбрать альтернативную комбинацию таких переменных. Например, для системы второго порядка, такой как масса-пружина или RLC-цепь, в качестве переменных состояния можно выбрать любые две линейно независимые комбинации xx{t) и x2(t). Так, для RLC-цепи мы могли бы принять за переменные состояния два напряжения, vc(/) и v; (/), где vL — напряжение на индуктивности. Тогда новые переменные состояния, х, их'2, будут связаны со старыми переменными хх и х2 соотношениями:
х =vc =х, , (3.11)
х* = Vj =vc - RiL =х, - Rx2. (3.12)
Уравнение (3.12) связывает напряжение на индуктивности со старыми переменными состояния vc и iL. В реальной системе всегда можно образовать несколько комбинаций переменных состояния, которые определяют энергию, запасенную в системе, и, следовательно, адекватно описывают ее динамику. На практике в качестве переменных состояния часто выбирают такие физические переменные, которые легко могут быть измерены.
Альтернативный метод получения модели в переменных состояния основан на использовании графа связей. Такие графы могут быть построены для электрических, механических, гидравлических и тепловых элементов или систем, а также для комбинаций элементов различных типов. Графы связей позволяют получить систему уравнений относи
тельно переменных состояния.
Переменные состояния характеризуют динамику системы. Инженера в первую очередь интересуют физические системы, в которых переменными являются напряжения, токи, скорости, перемещения, давления, температуры и другие аналогичные физические величины. Однако понятие состояния применимо к анализу не только физических, но также биологических, социальных и экономических систем. Для этих систем понятие состояния не ограничивается рамками представлений об энергии и подходит к переменным состояния в более широком смысле, трактуя их как переменные любой природы, описывающие будущее поведение системы.
|
Ъи...bt |
|
1т |
|
(3.14) |
|
Ъпі...Ъпт |