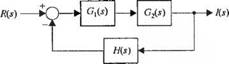
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Пример синтеза с продолжением: система чтения информации с диска
|
□ |
В разд. 1.12 мы поставили исходную задачу управления дисководом: позиционировать считывающую головку точно на заданную дорожку и при возможности обеспечить переход от одной дорожки к другой в пределах 10 мс. В этой главе мы выполним этапы 4 и 5 процесса синтеза (см. рис. 1.19).
Нам необходимо выбрать исполнительное устройство, датчик и регулятор (этап 4). Затем следует разработать модель объекта, G(s), и датчика. Для приведения в действие
Рис. 2.65
|
Рычаг |
|
Пластина |
|
Г оловка |
|
Двигатель |
|
|
Считывающая головка дисковода
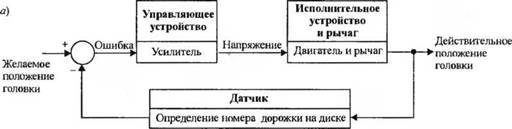
рычага считывающей головки используется двигатель с постоянными магнитами (см. рис. 1.24). При производстве дисководов его называют двигателем со звуковой катушкой. Головка считывания закреплена на скользящем элементе, закрепленном на рычаге, как показано на рис. 2.65. Гибкая пластина дает возможность головке плавать над диском с зазором менее 100 нм. Тонкопленочная головка воспринимает магнитный поток и формирует сигнал, поступающий на усилитель. Сигнал ошибки на рис. 2.66(a) формируется на основании заданного номера дорожки. Полагая, что положение считывающей головки определяется точно, можно считать, что передаточная функция датчика H(s) = I, как показано на рис. 2.66(б). На этом рисунке также приведены модели двигателя с постоянными магнитами и линейного усилителя. Двигатель, управляемый по цепи якоря, достаточно хорошо представляется в виде модели на рис. 2.20 при Кь = 0. В полной модели системы на рис. 2.66(б) предполагается, что пластина является жесткой, а не слишком гибкой. В гл. 4 мы рассмотрим модель, в которой это допущение не имеет силы.
|
|
|
б) |
|
ад |
|
О |
|
R(S) ■ |
|
Усилитель |
Двигатель и рычаг G(s) |
|
|
К„ |
— К,, |
|
|
s(Js+b)(Lsi R) |
Датчик
ж*)=1
Рис. 2.66. Структурная схема считывающей системы дисковода
|
Таблица 2.9. Типичные параметры дисковода
|
Типичные параметры дисковода приведены в табл. 2.9. Следовательно, мы имеем:
Кт 5000
G(s)=-
s(Js+b)(Ls + R) s(s + 20)(s +1000) Выражение G(s) можно также представить в виде
G(s)=-
|
K„/bR |
(2.117)
|
s(tLs+ 1)(ts+ 1) |
(2.118)
гдет£=J/b= 50 мс их = L/R = I мс. Поскольку мы можем пренебречь величиной х.
Тогда
KJbR 0,25
G(S):
|
или |
5(tls+1) s(0,05s+1) G(s) = - 5
i(s+20)
Структурная схема замкнутой системы приведена на рис. 2.67. На основании правил преобразования структурных схем (см. табл. 2.6) можно записать:
Y(s) KaG(s)
(2.119)
R(s) 1 + KaG(s)
Используя аппроксимацию G(s) вторым порядком, мы получим
Y(s)
5К„
|
Если Ка = 40, то |
R(s) s2+20s+5Ka' R(s).
200
Y{s) =
s2 +20i + 200
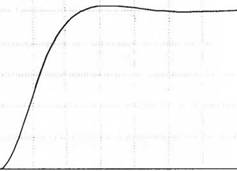
Полагая r(t) = 0,1 рад, т. e. R(s) = 0,1/s, с помощью функции step мы получим реакцию системы, изображенную на рис. 2.68.
|
-О |
|
к., |
|
ад |
|
Рис. 2.67 Структурная схема замкнутой системы |
Рис. 2.68
|
0.3 0.4 Время (с) |
Реакция системы, изображенной на рис. 2.67, на воздействие R(s) = 0,1/s
Резюме
В этой главе были рассмотрены количественные математические модели систем управления и их элементов. При построении этих моделей в основу были положены дифференциальные уравнения, описывающие поведение физических систем. В числе этих систем были рассмотрены механические, электрические, гидравлические и термодинамические. В отношении нелинейных элементов был применен метод линеаризации, основанный на разложении нелинейной функции в ряд Тейлора в окрестности рабочей точки. После такой линеаризации к системе применимо преобразование Лапласа и вытекающее из него понятие передаточной функции. С помощью передаточной функции исследователь может определить реакцию системы на различные входные воздействия. Было также показано, как образуются модели систем в виде структурных схем и сигнальных графов. Продемонстрировано, как с помощью формулы Мейсона можно получить связь между отдельными переменными системы сложной конфигурации. Преимущество моделей в виде сигнальных графов заключается в том, что формула Мейсона позволяет получить связь между переменными системы, не прибегая к сложным преобразованиям. Итак, в этой главе мы получили такие ценные средства описания систем управления, как их математические модели в виде передаточных функций, структурных схем и сигнальных графов. Мы оценили также преимущества компьютерного моделирования для исследования поведения систем при различных комбинациях их параметров и внешних воздействий. И, наконец, мы продолжили разработку системы управления считыванием информации с диска, получив передаточные функции элементов этой системы.
Упражнения
У-2.1. В системе с единичной отрицательной обратной связью, изображенной на рис. 2.1 (У), нелинейный элемент описывается зависимостью у = /(е) = е~. При задании входного сигнала в диапазоне от 0 до 4 постройте график зависимости у(г) как для разомкнутой, так и для замкнутой системы и покажите, что при наличии обратной связи характеристика становится более линейной.
а
L
f(e)
Обратная связь действует при замыкании ключа
Рис. 2.1 (У). Разомкнутая и замкнутая система
|
У-2.2. Сопротивление термистора R описывается зависимостью я = /v0J7', где R0 = 10 кОм, а Т—температура в градусах Цельсия. Получите линейную модель термисто- У-2.3. Механическая система пружина-масса, У-2.4. Для быстрого вывода на печать документов 5(s+ 100) |
|
2 1 |
Разрыв X пружины / і ( і w Перемещение |
|
-3 -2 -1 V |
і 4 г * 1 2 3 (СМ) |
|
/л |
|
|
/ -2 |
|
|
Сжатие j |
|
|
пружины -3 |
|
Сила |
|
Рис. 2.3 (У). Характеристика пружины |
|
Y(s)- |
|
-R(s). |
|
+ 60^+500 единичное ступенчатое воздействие, то каков закон изменения положения луча |
|
(а) Если r(t) У(Ф (б) Чему равно конечное значение >"(/)? Ответ: (а) у(1) = 1 - 1,125е"10' + 0,125е-50': (б) yss = 1. литель на ОУ. Считая операционный усилитель |
|
|
|
Рис. 2.5 (У). Неинвертирующий усилитель |
|
. R2 1+ — . Ri. |
|
Ответ: — = Vi |
|
R, |
|
У-2.6. Нелинейное устройство описывается зависимостью у= f(x) = - їх. Рабочая точка задана значением входной переменной х0 = 1/2. Получите линейную аппроксимацию характеристики в случае малых отклонений Ах. Ответ: Ay = Ax/sfl. У-2.7. Для поддержания постоянной яркости свечения лампы накаливания используется фототранзистор, включенный в цепь обратной связи. При уменьшении напряжения в сети яркость лампы также уменьшается и фототранзистор Qt вырабатывает меньший ток. В результате увеличивается проводимость мощного транзистора, управляющего зарядом конденсатора. Напряжение конденсатора подается непосредственно на лампу. На рис. 2.7(У) изображена структурная схема этой системы. Определите передаточную функцию I(s)/R(s), где I(s) — яркость лампы, a R(s) — управляющий сигнал, соответствующий желаемому значению яркости. У-2.8. В 1930-е годы инженер Н. Минорский разработал для ВМС США новую систему управления курсом судна. Эта система представлена на рис. 2.8(У) в виде структурной схемы, где Y(s) — |
|
Фильтр |
|
б) |
|
а) |
|
|
|
Рис. 2.7 (У). Регулятор яркости |
|
Л |
|
Непрозрачная трубка |
|
Диафрагма |
т
|
Рис. 2.8 (У). Система управления курсом судна |
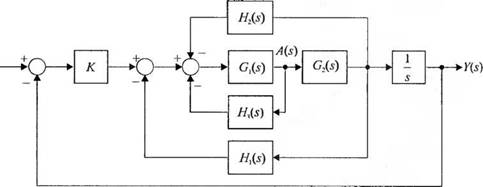
курс судна, R(s) — заданное значение курса, aA(s) — угловое положение руля. Определите передаточную функцию Y(syR(s).
Ответ, М =---------------------------- ^;,(.vX;2(.v)/.v--------------------------
R(s) 1 + Gi(s)H3(s) + Gl(s'jG2(s)[Hl(s) + H2(s)]+ KGl(s)G2(s)/ s
|
|
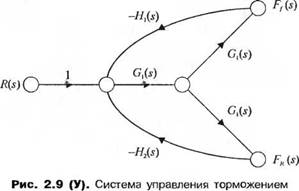
У-2.9. В системе торможения автомобиля применяется электронная цепь обратной связи, с помощью которой автоматически вырабатывается тормозное усилие на каждое из колес. На рис. 2.9(У) приведен упрощенный сигнальный граф этой системы, где F/ (s) и Ftt(s) есть, соответственно, тормозные усилия на передние и задние колеса, a R(s) — желаемая реакция автомобиля на скользкой дороге. Определите передаточную функцию Fj(s)/R(s).
У-2.10. Опыт эксплуатации внедорожных автомобилей показывает, что при движении по пересеченной местности они подвергаются действию многих возмущений. В этом случае может быть применена система активной подвески,
управляемая с помощью датчика, который предвидит изменение дорожной обстановки. Пример такой простой системы, смягчающей влияние неровностей, приведен на рис. 2.10(У). Определи-
|
D(s) |
Возмущение (ухаб, неровность) Предварение возмущения
D(s)
|
Подпрыгивание автомобиля или отклонение от горизонтали |
|
ОД |
|
G(s) |
|
Желаемое |
ад ; |
К, |
кг |
+ .. W/ |
|
отклонение |
j * |
--- + |
|
6- |
|
Динамика автомобиля |
Рис. 2.10 (У). Система активной подвески
|
-20 -30 -40 |
|
1 2 3 х. Отклонение (см) |
|
|
|
У- |
|
-2 Рис. |
|
-I 2.11 |
|
(У). Характеристика пружины V |
|
Управляющий сигнал Цилиндр |
|
Электр сре, |
ОДВІ іукт< |
ігатель )ром ,, |
|
I |
—----- / |
|
|
Un |
эрше |
НІ |
|
Плунжер |
|
Регулятор |
|
Демпфи рующее отверстие |
|
_ Жидкость Выход датчика |
|
Шток поршня'' |
|
Ход поршня |
|
Рис. 2.12 (У). Амортизатор |
|
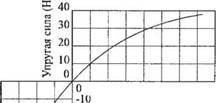
те значение коэффициента Ки при котором У-2.11. Зависимость упругой силы от деформа- Определите значение коэффициента упру- (а) х0 = - 1,4; (б) х0 = 0; (е) х0 = 3,5. У-2.12. Одной из наиболее полезных автомоби- новение упругой и демпфирующей Разработайте линейную модель амортизатора в виде структурной схемы. У-2.13. Определите передаточную функцию У,(.у)/Л,(ї) для многомерной системы, изображенной У-2.14. Запишите дифференциальные уравнения относительно токов і, и /2 для схемы, изображен- |
|
Рис. 2.13 (У). Многомерная система |
|
|
|
У-2.15. Система управления положением космической платформы описывается следующими уравнениями: Yw* аг |
|
г+25.4,-в |
V=r-p,
|
7v,. |
dQ пл — = 0,6v,,
dt 2
Рис. 2.14 (У). Электрическая схема Переменные в уравнениях имеют следующий смысл:
r(t) — желаемое положение платформы. p(t) — действительное положение платформы, vt(/) — напряжение на входе усилителя, v2(t) — напряжение на выходе усилителя,
0(0 — положение вала двигателя.
Изобразите сигнальный граф системы, обозначив все элементы и указав связь между ними; затем определите передаточную функцию системы P(s)/R(s) .
У-2.16. Пружина, используемая в автомобильном амортизаторе, создает силу f определяемую уравнением f=h?, где х—деформация пружины. Получите линейную модель пружины при х0 = 1. У-2.17. Выход у и вход х устройства связаны соотношением
у = х + 0,79л:3.
(а) Определите значения выходной переменной в двух рабочих точках: х0 = I к х0 = 2.
(б) Получите линеаризованные модели устройства в этих рабочих точках и сравните их. У-2.18. Передаточная функция системы имеет вид:
Г(д)_ 10(5+2)
R(s) ~ j2 + 8j + 15
Определите }'(ґ), если r(t) имеет вид единичной ступенчатой функции.
Ответ: y(t) = 1,33 + 1,67е~3( — Зе~5/.
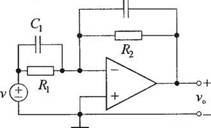
У-2.19. Определите передаточную функцию V0(s)!V(s) для схемы на операционном усилителе, изображенной на рис. 2.19(У). Считайте, что операционный усилитель — идеальный. Вычислите передаточную функцию при Rx-R2= 100 кОм, С, = 10 мкФ и С2 = 5 мкФ.
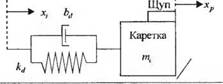
У-2.20. На рис. 2.20(У) изображена скользящая каретка, обеспечивающая прецизионное позиционирование щупа. Определите передаточную функцию Хр (s)/X, (s), если коэффициент трения приводного вала bd= 1, коэффициент упругости приводного вала kd = 3, тс = 2/3 и коэффициент трения скольжения bs = 1.
|
Рис. 2.19 (У). Схема на операционном усилителе |
С,
|
|
|
Трение скольжения, b% |
|
Рис. 2.20 (У). Каретка с прецизионным позиционированием |
|
-і
Рис. 2.22 (У) |
|
Рис. 2.21 (У). Спутник |
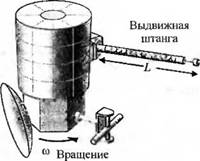
У-2.21. Угловая скорость вращения спутника со, изображенного на рис. 2.21(У), зависит от длины штанги L. Передаточная функция, связывающая co(s) и приращение длины штанги ДL(s), имеет вид:
сф) _ 2,5(5+ 2)
AL(s) ~ (л-+ 5)(л-+ I)2 ’
Изменение длины штанги происходит в соответствии с выражением AL(s) = 114s. Определите закон изменения скорости со (t).
,,1 3 _* 35 5
Ответ: (ait) =—і--------------------- е е te.
4 128 128 32
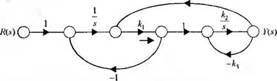
У-1.11. Определите передаточную функцию замкнутой системы T{s) = Y(s)IR(s), соответствующую сигнальному графу на рис. 2.22(У).
|
10 |
1 5 |
|
|
І+ 1 |
||
|
-► У(і) |
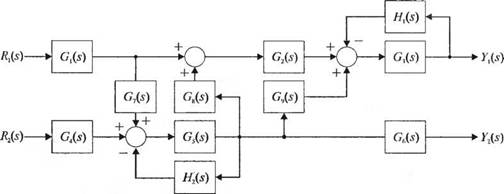
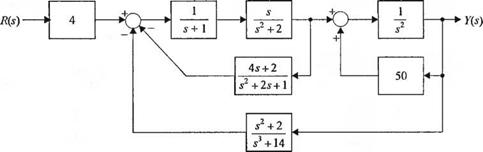
У-2.23. На рис. 2.23(У) изображена структурная схема системы. Определите передаточную функцию системы T(s) =
= Y(s)/R(s).
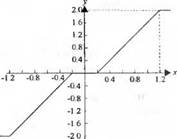
У-2.24. Усилитель может обладать зоной нечувствительности, как показано на рис.
|
№ |
|
Рис. 2.23 (У) |
2.24(У). Для линейного участка характеристики воспользуйтесь аппроксимацией вида. у = ах3. Выберите значение а и линеаризуйте характеристику усилителя в окрестности рабочей точки х = 0.6.
У-2.25. Определите передаточную функцию X2(s)/F(s) для системы, изображенной на рис. 2.25(У). Оба груза скользят по повехности без трения, а коэффициент жесткости пружины к - 1 Н/м.
... 1
|
Рис. 2.24 (У). Усилитель с зоной нечувствительности |
Ответ:
|
F(s) |
s2(s2 + 2) '
|
----- ► *! |
----- ► |
|||
|
т —► |
т, 1 кг |
к vwwv^ |
т 2 1 кг |
|
" " ' Рис. 2.25 (У) |
|
|
|
Рис. 2.26 (У) Система при наличии возмущения |
|
D(s) |
У-2.26. Определите передаточную функцию Y(s)/D(s) для системы, изображенной на рис. 2.26(У). У-2.27. Определите передаточную функцию VQ(s)IV(s) для схемы на операционных усилтелях, изображенной на рис. 2.27(У). если R, = 167 кОм, R2 = 240 кОм, Л3 = 1 кОм, R4 = 100 кОм и С = 1 мкФ. Операционные усилители считаются идеальными.
|
о + |
|
|
Рис. 2.27 (У)
Схема на операционных усилителях
|
Рис. 2.28 (У) |
|
|
|
1 |
ь |
|
|
/ * |
5 + 5 |
|
1 Ї+ 10 |
|
Y(s) |
|
О г |
|
од |
|
б) R{s) - |
|
-►од |
|
ад |
|
У-2.28. Для стуктурной схемы на рис. 2.28(У)(б) определите G(s) и H(s) так, чтобы эта схема была эквивалентна структурной схеме на рис.2.28(У), (а). Для схемы на рис. 2.28(У), (б) запишите передаточную функцию Y(s)/R(s). У-2.29. Для системы на рис. 2.29(У): (а) Определите передаточную функцию Y(s)/R(s), если G(s) = - 10 |
|
а |
|
ОД) |
|
ад- |
|
-►ОД |
|
(iz + 2j+10) (б) Запишите выражение У(ї), если входной |
|
Рис. 2.29 (У) |
|
сигнал r(t) есть единичная ступенчатая функция. (в) Найдите выражение y(t). У-2.30. Найдите вычеты для разложения К(л) на простые дроби путем (а) вычислений и (б) графических построений на ^-плоскости: V (з) = 400------- . s + 8j + 400 |
|
Задачи |
|
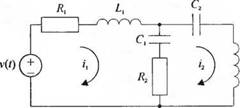
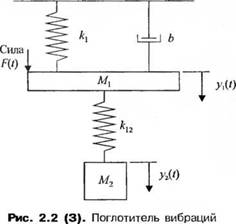
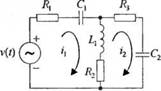
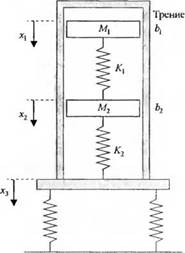
3-2.1. Запишите систему интегродифференциальных уравнений, характеризующую процессы в электрической схеме на рис. 2.1(3). 3-2.2. На рис. 2.2(3) изображен динамический поглотитель вибраций. Подобная схема типична для многих ситуаций, связанных с вибрацией механизмов, содержащих несбалансированные компоненты. Параметры М2 и к]2 можно подобрать так, что основная масса Mi будет избавлена от вибраций при F(t) = flsinto0r. Запишите дифференциальные уравнения, описывающие поведение системы. 3-2.3. На рис. 2.3(3) изображена система из двух масс, соединенных пружиной. Предполагается, что массы и пружины одинаковы. Запишите дифференциальные уравнения, описывающие поведение системы. |
|
|
|
3-2.4. Нелинейный усилитель описывается следующей зависимостью: V,2, v, > О, -V,2, v, < 0. |
|
В рабочей точке входное напряжение изменяется в диапазоне ± 0.5 В. Получите линейную ап- 3-2.5. Поток жидкости через трубку можно описать нелинейным уравнением Q = А'ОР, - Р2)т. где К = const, а смысл остальных переменных ясен из (а) Получите линейную аппроксимацию для уравнения по- (б) Что произойдет с полученной аппроксимацией, если ра- 3-2.6. С помощью преобразования Лапласа получите выражение для тока /2(s) из задачи 2.1. если |
|
|
|
Рис. 2.1 (3). Электрическая схема |
|
. V,(/) • -*,(') |
|
• V,{/) • .ф) |
|
Сила т -♦і |
|
-Wth м ЧіШЬ |
|
м ил |
|
І о о * |
|
Рис. 2.3 (3). Система с двумя массами |
|
Vo(0 = |
|
|
|
Рис. 2.5 (3). Поток жидкости через трубку |
|
|
|
т |
|
с |
|
Рис. 2.8 (3). Мостовая Т-образная схема |
|
-о + к |
|
X |
|
+ о- |
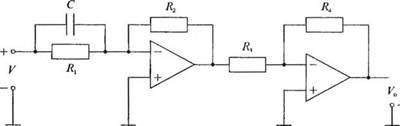
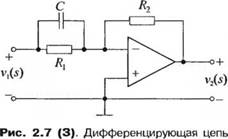
3-2.7. Получите передаточную функцию для дифференцирующей цепи, изображенной на рис. 2.7(3).
3-2.8. В системах управления, работающих на переменном токе, в качестве фильтра часто применяются мостовые Т-образные схемы. Одна из таких схем приведена на рис. 2.8(3). Покажите, что передаточная функция этой схемы равна
V0 (s) _ 1 + 2Rfs + RiR2C2s2
V,(s) ~ 1+ (2R + R2)Cs + R]R2C2s2 '
Укажите расположение на комплексной плоскости полюсов и нулей, если R, = 0,5, R-, = 1 и С =0,5.
3-2.9. Получите передаточную функцию X^syFfs) для системы с двумя связанными массами из задачи 2.3. Определите положение на s-плоскости полюсов и нулей, если М = 1. b/k = 1 и
С = ——7=— = °-1 - 2 л/Ш
3-2.10. Определите передаточную функцию Y{(s)/F(s) для поглотителя вибраций из задачи 2.2. Установите, при каких значениях параметров М2 и кп в случае Fit) = a sinco0f вибрация массы Мх будет отсутствовать.
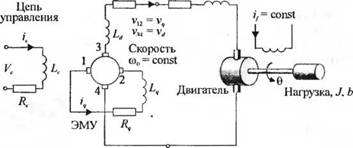
3-2.11. В электромеханических системах, требующих значительного усиления по мощности, часто применяются электомашинные усилители (ЭМУ). Такой ЭМУ и сервопривод изображены на рис. 2.11(3). Определите передаточную функцию б(s)/Vc(s) и изобразите структурную схему системы. Считайте, что vcl = кгіч и vq = kxic.
|
Рис. 2.11 (3). Электромашинный усилитель и двигатель, управляемый по цепи якоря |
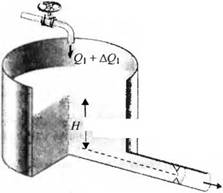
3-2.12. На рис. 2.12(3) изображена емкость, в которую поступает несжимаемая жидкость. Можно считать, что изменение расхода на выходе из емкости, AQ2. пропорционально изменению уровня жидкости АН. В установившемся режиме Q, = Q2 и Q2 = k-JW. Используя линейную аппроксимацию, получите передаточную функцию объекта AQ2{s)/AQl(s).
|
Входной вентиль |
|
+ АН |
|
Отверстие |
|
0.2 + AQz Рис. 2.12 (3). Система с потоком жидкости |
|
|
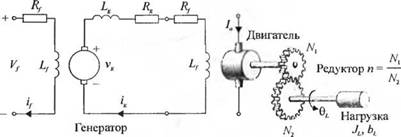
3-2.13. На рис. 2.13(3) изображена разомкнутая электромеханическая система управления. Генератор, якорь которого вращается с постоянной скоростью, вырабатывает напряжение, поступающее на обмотку возбуждения двигателя. Двигатель обладает моментом инерции Jm и коэффициентом трения Ът. Определите передаточную функцию 6;(s)/V As) и изобразите структурную схему системы. Предполагается, что напряжение генератора vg пропорционально току возбуждения if.
|
Рис. 2.13 (3). Система генератор-двигатель |
3-2.14. Двигатель постоянного тока с управлением по цепи возбуждения через редуктор приводит во вращение нагрузку. Характеристика двигателя предполагается линейной. В результате испытаний при подаче на обмотку двигателя ступенчатого напряжения величиной 80 В нагрузка через 0,5 с достигает скорости 1 рад/с . Установившееся значение скорости равно 2,4 рад/с. Определите передаточную функцию двигателя B(s)/Vf(s) с размерностью рад/В. Индуктивностью обмотки возбуждения можно пренебречь (см. рис. 2.17).
|
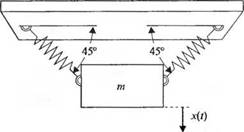
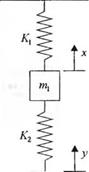
Рис. 2.15 (3). Масса на пружинных подвесках |
3-2.15. Рассмотрите систему масса-пружины, изображенную на рис. 2.15(3). Получите дифференциальное уравнение, описывающее движение массы т. Найдите реакцию системы на начальное условие х(0)= 1.
3-2.16. Постройте сигнальный граф для следующей системы алгебраических уравнений, считая Х| и х2 зависимыми пере - меными, аби 11 — входами:
JC| + 1.5дг2 = 6,
2дС| + 4х1 =11.
По формуле Мейсона определите значение каждой зависимой переменной. Решение для х, проверьте с помощью правила Крамера.
|
Рис. 2.17 (3). Механическая система |
3-2.17. На рис. 2.17(3) изображена механическая система. в которой задается смещение х/1) известного вида относительно стационарного значения этой переменной.
(а) Запишите два независимых уравнения движения.
(б) Получите уравнения движения в виде преобразований Лапласа, считая начальные условия нулевыми.
(в) Изобразите сигнальный граф, соответствующий этой системе уравнений.
(г) С помощью формулы Мейсона найдите связь между Х,(х) и X3(i). Tu(s). Сравните трудоемкость получения 4 з 0s) с помощью матриц и с помошыо формулы Мейсона.
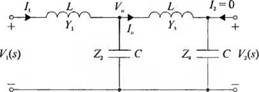
3-2.18. На рис. 2.18(3) изобажена каскадная LC-цепь, для которой справедливы следующие уравнения:
|
h = (Уі - К, )Г» |
v„ = (/, - /„ )Z2.
У2
|
4 = (К, ~ у2 т, |
= 4 z4.
Изобразите сигнальный граф, соответствующий этим уравнениям, и определите передаточную функцию F2(s)/K,(s).
|
|
Рис. 2.18 (3)
Каскадная LC-цепь

|
|
|
Рис. 2.19 (3). Схема на неинвертирующем операционном усилителе |
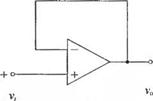
3-2.19. На рис. 2.19(3) изображен повторитель напряжения (буферный усилитель). Считая операционный усилитель идеальным, покажите, что Т - v0/v, = 1.
|
Т |
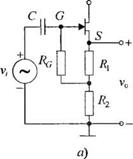
3-2.20. Повторители напряжения используются для существенного уменьшения выходного сопротивления источника сигнала. Схема такого повторителя на полевом транзисторе с коэффициентом усиления, практически равным единице, приведена на рис. 2.20(3) (а), а его малосигнальная эквивалентная модель — на рис.2.20(3) (б). Предполагается, что для создания смещения выбрано R2 » Rt и что Rg » R2.
(а) Получите выражение лля коэффициента усиления схемы.
(б) Вычислите коэффициент усиления, если gm = 2000 мкмо и Rs = 10 кОм, где /?„. = Rt + R2 .
(в) Изобразите сигнальный граф, отражающий уравнения для данной схемы.
|
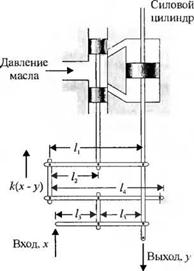
Рис. 2.21 (3). Гидравлический сервопривод |
|
|
|
Рис. 2.20 (3) Повторитель напряжения на полевом транзисторе (схема с общим стоком). |
|
Q G V |
~^Smvgs . s „| |
|
i> N |
Г Л |
|
б) |
3-2.21. На рис. 2.21(3) изображен гидравлический сервопривод с механической обратной связью. Площадь поршня силового гидроцилиндра равна А. Когда золотник перемещается на малую величину Дг, то масло потекает через гидроцилиндр со скоростью pAz. где р— степень открытия отверстия. Давление масла предполагается постоянным. Из геометрических со
|
-Ух-у)--у. ч |
ображений ясно, что Az = k
(а) Изобразите сигнальный граф замкнутой гидромеханической системы.
|
|
|
Рис. 2.22 (3). Стержни длиной L, соединенные пружиной в точках Z./2 |
|
М |
(б) Определите передаточную функцию замкнутой системы y(s)ZY(s).

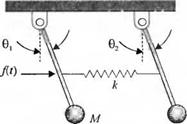
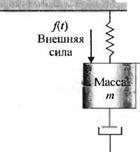
3-2.22. На рис. 2.22(3) показаны два маятника, соединенные пружиной точно в середине стержней, причем в их точках подвеса трение отсутствует. Предполагается, что каждый маятник представляет собой массу М на конце стержня длиной L, а массой стержня можно пренебречь. Кроме того, считается, что отклонения от положения равновесия являются малыми, поэтому для sinG и cosG применима линейная аппроксимация. При 0] = 02 деформация пружины отсутствует. Внешняя сила fit) приложена только к левому стержню.
(а) Запишите уравнения движения и представьте их в виде структурной схемы.
(б) Определите передаточную функцию T(s) = 0,(s)/F(s).
(в) Изобразите расположение на s-плоскости полюсов и нулей T{s).
3-2.23. На рис. 2.23(3) изображена малосигнальная эквивалентная схема транзисторного усилителя с общим эмиттером. Обратная связь в усилителе осуществляется с помощью резистора Rj. Определите отношение vce/vr
|
Рис. 2.23 (3) Усилитель с общим эмиттером |
|
К, |
|
+ h,„ V, |
|
+ V' |
|
К |
|
і-ч 4-н (~) v„ |
|
|
I
|
|
Рис. 2.24 (3). Усилитель с обратной связью
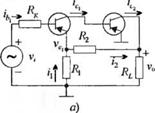
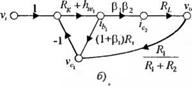
3-2.24. На рис. 2.24(3), (а) изображен усилитель напряжения с обратной связью на двух соединенных последовательно транзисторах. В эквивалентной схеме для переменного тока опущены резисторы, необходимые для задания смещения, и шунтирующие конденсаторы. Соответствующий этой схеме сигнальный граф приведен на рис.2.24(3), (б). На графе не отражено влияние И,.е. обычно достаточно точно аппроксимируемого, а также предполагается, что (Л7 + Л; )» Л,.
(а) Определите коэффициент усиления по напряжению v0/v;.
(б) Определите коэффициент усиления ПО току
(в) Определите входное сопротивление vjib.
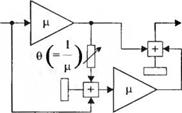
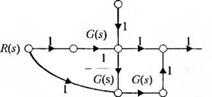
3-2.25. Часто не обращают внимание на тот факт, что Г. С. Блэк, предложивший в 1927 г. идею разработки усилителей с отрицательной обратой связью, тремя годами раньше изобрел метод синтеза схем, известный как метод коррекции по возмущению. Дальнейшие эксперименты показали, что этот метод открывает богатые возможности для создания усилителей с высокостабильными характеристиками. Усилитель Блэка изображен на рис. 2.25(3) (о) в том виде, как он был предложен им в 1924 г. Соответствующий сигнальный граф приведен на рис. 2.25(3), (б). Определите передаточные функции от входа R(s) к выходу У(а) и от возмущения Да) к выходу У(а). Каждому усилителю, обозначенному как ц на схеме (а), соответствует D(s) на графе.
|
|
|
|
|
ОВД |
|
Рис. 2.25 (3). Усилитель Г. С. Блэка |
|
а) б) |
Да)
3-2.26. Если рука робота захватывает тяжелый груз, то в ее сочленениях появляется значительная гибкость. На рис. 2.26(3) изображена соответствующая данному случаю модель руки робота. Определите передаточную функцию Y(s)/F(s).
|
► х |
ь |
+ У |
|
|
М |
------- 1 |
т |
|
|
-WWAA- |
|
F(t) |
|
|
|
Рис. 2.26 (3)_ Модель руки робота в виде демпфированной системы «масса-пружина» |
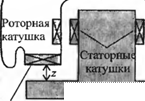
Ъ-1.21. Транспортные средства на магнитной подушке отличаются большей скоростью и меньшим трением по сравнению с традиционным железнодорожным транспортом. На рис. 2.27(3) схематически изображен поезд, плавающий над магнитным рельсом с воздушным зазором. Сила левитации FL регулируется током і в катушках подвески и может быть аппроксимирована выражением
|
□Роторная гУкатушка |
|
МагнитопровоЯ |
|
Катушка подвески |
|
Рис. 2.27 (3). Поезд на магнитной подушке (в разрезе) |
|
|
п-4.
где z — величина воздушного зазора. Эта сила направлена навстречу силе тяжести F = mg. Определите линеаризованную зависимость между воздушным зазором z и управляющим током в окрестности точки равновесия.
|
Катушка подвески |
3-2.28. Многоконтурная модель экологической среды обитания в городских условиях может включать в себя следующие переменные: количество населения (Р). благоустройство (Л/), приток населения в город (С), санитарные возможности (5). количество заболеваний (£>), число бактерий на единицу площади (В) и количество отходов на единицу площади (С). В скобках указан символ каждой переменной. Можно предположить наличие следующих замкнутых причинно-следственных цепочек:
I. Р G В D —> Р 3. P—>M—>S—*D—*P;
г. р^м-*с^>р: 4. p->m->s->b->d->p.
|
Момент двигателя |
|
Шарик |
|
|
Изобразите сигнальный граф, отражающий эти связи, и укажите на нем соответствующие коэффициенты преобразования. Поясните, почему вы считаете каждое преобразование положительным или отрицательным. Например, преобразование S —» В является отрицательным, т. к. улучшение санитарных условий ведет к уменьшению числа бактерий на единицу площади. В каком из четырех контуров обратная связь является положительной и в каком — отрицательной?
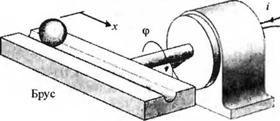
3-2.29. Мы хотим удержать в равновесии шарик, который может катиться по вращающемуся брусу, как показано на рис. 2.29(3). Предположим, что вращающий момент двигателя определяется входным током і и при этом трением можно пренебречь. Будем также считать, что брус можно удержать в равновесии вблизи горизонтального положения (ф = 0), так что отклонения угла ф являются малыми.
Определите передаточную функцию X(s)/I(s) и приведите структурную схему, на которой обозначьте <p(i). X(s) и I(s).
3-2.30. Точность систем управления в значительной степени определяется типом датчика, используемого в цепи обратной связи. Особенно важную роль играют динамические свойства датчика. Большинству датчиков свойственна передаточная функция
Рассмотрите некоторые из современных промышленных датчиков и выявите, какой точностью и постоянной времени они обладают. Как пример, возьмите по два из следующих датчиков: (1) линейного перемещения. (2) температуры, (3) деформации, (4) давления.
|
|
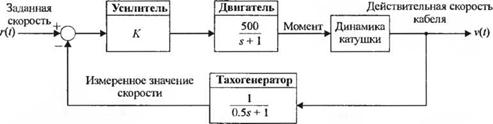
Рис - 2.31 (3). Система управления скоростью сматывания кабеля с катушки
3-2.31. В системе, управляющей скоростью, с которой кабель сматывается с катушки, в качестве датчика используется тахогенератор. Выходное напряжение тахогенератора используется для управления скоростью двигателя, вращающего катушку. На рис. 2.31(3) изображена соответствующая система управления. Радиус катушки равен 4 м. когда она заполнена, и 2 м — когда она пустая. Момент инерции катушки J = 18.5/?4 - 221. Скорость изменения радиуса
(1R _ Р2ы dt 2п W
|
-Я, |
|
+н2 |
где W— ширина катушки, a D — диаметр кабеля. Действительная скорость сматывания кабеля v(t) = ГШ Заданная скорость сматывания равна 50 м/с. Разработайте схему моделирования этой системы на цифровом компьютере и определите ее реакцию на интервале 0-20 с для трёх значений коэффициента К = 0,2: 0.4 и 0,6. Угловая скорость катушки со = dQ/dt равна интегралу от момента с коэффициентом 1/J. Обратите внимание, что момент инерции изменяется по мере разматывания кабеля, однако при моделировании это будет учтено приведенным выше выражением. Выберите коэффициент К так. чтобы ограничить перерегулирование величиной 9% и в то же время добиться максимального быстродействия. Для моделирования примите, что при t = 0 W = 2.0, D = 0,1 и R = 3,5.
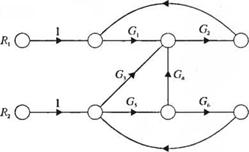
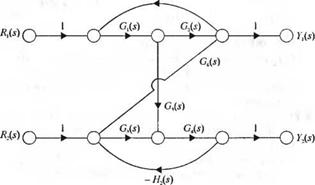
3-2.32. На рис. 2.32(3) изображена система с двумя входами и двумя выходами. Полагая Л, = 0, определите y,(s)/7?|(s) и
адад-
|
|
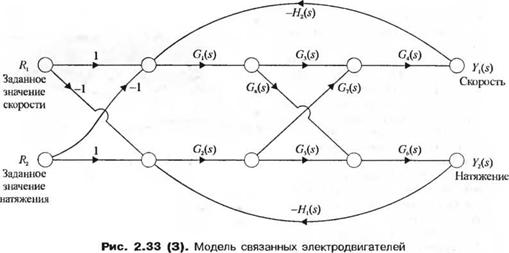
3-2.33. Система состоит из двух электродвигателей, соединенных между собой непрерывным гибким ремнем. Ремень также проходит через специальное приспособление, измеряющее его скорость и натяжение. Задача управления состоит в регулировании скорости и натяжения ремня путем изменения вращающих моментов двигателей.
Практическим примером такой системы может служить перемотка пряжи в текстильном производстве с одной бобины на другую с высокой скоростью. В промежутке между двумя бобинами пряжа подвергается определенной обработке, при которой может потребоваться регулирование в заданных пределах скорости и натяжения. Модель подобной системы приведена на рис. 2.33(3). Определите Y2{s)/R,(s). Определите также, при каких условиях, предъявляемых к системе, У2 не будет зависеть от Л,.
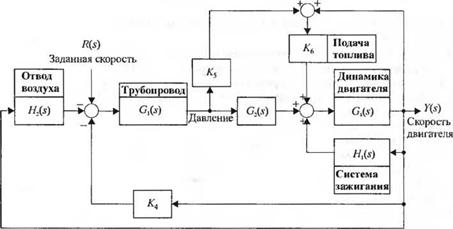
3-2.34. Определите передаточную функцию Y(s)/R(sJ для системы регулирования скорости (числа оборотов) на холостом ходу автомобильного двигателя с инжекцией топлива, изображенной на рис. 2.34(3).
|
|
|
_________ ^-Профиль 'дороги |
|
Рис. 2.35 (3). Подвеска колеса автомобиля-пикапа |
|
|
|
|
|
Рис. 2.36 (3) |
|
12 /+8j~ + 19j + 12 |
|
-> Y(s) |
|
т- |
|
Рис. 2.37 (3) |
|
|
|
>1 |
|
|
1 I 1 |
т2 |
|
1 |
4* |
|
I и |
|
0,5 м ■ |
|
■Q |
|
о- |
|
Рис. 2.38 (3) Система с двумя массами |
|
3-2.35. На рис. 2.35(3) изображена система Масса автомобиля равна /и,, а масса Определите передаточную функцию 3-2.36. Система управления с обратной свя- нуюфункцию Y(s)/R(s): (а) путем время переходная функция достигает 90% от своего установившегося значения? 3-2.37. Для системы, представленной на рис. 2.37(3): (а) Разложите передаточную функцию на эле- (б) Постройте график полученной функции (в) Определите импульсную переходную функцию системы y(t) для (г) Постройте график импульсной переходной функции и найдите ее 3-2.38. На систему с двумя массами, изображенную на рис. 2.38(3), действу- 3-2.39. Крутящийся маятник, изображенный на рис.2.39(3). состоит из двух Стержень подвешен на тонкой проволочке, |
амплитуды 10 градусов? Проволочка имеет коэффицент упругости при скручивании, равный 2 ■ 10-4 Н • м/рад, а коэффициент вязкого трения шариков в воздухе также равен 2 • 10-4 Н • м/рад. Масса каждого шарика равна 1 кг.
|
|
Рис. 2.40 (3)
Электрическая схема
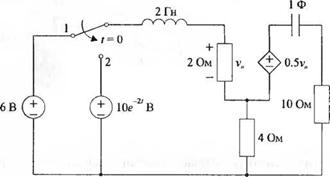
3-2.40. В схеме, изображенной на рис. 2.40(3), определите изображение по Лапласу выходного напряжения К0(у). Предполагается, что при / < 0 схема находится в установившемся состоянии, а в момент / = 0 ключ мгновенно переводится из положения 1 в положение 2.
|
Рис. 2.41 (3). Демпфирующее устройство в разрезе |
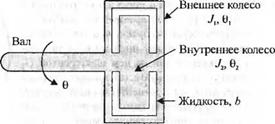
3-2.41. Для уменьшения нежелательных
вибраций механизмов применяются демпфирующие устройства. На рис. 2.41(3) показано одно из таких устройств: между двумя колесами помещается вязкая жидкость, например густое масло. Когда вибрация становится значительной, движение колес относительно друг друга создает демпфирующий эффект. Если механизм вращается без вибрации, то относительное движение колес отсутствует и демпфирования не происходит. Опре-
|
Заданная Действительная
|
делите 0|(х) и 02(у). Коэффициент упругости вала равен К, коэффициент вязкого трения — Ь. а вращающий момент, передаваемый нагрузке — Т.
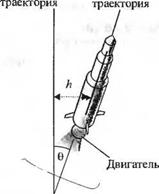
3-2.42. На рис. 2.42(3) изображена ракета, оснащенная двигателем с изменяемым вектором тяги. Отклонение ракеты по горизонтали от заданной траектории равно h, а скорость ее движения в направлении оси равна V. Момент, развиваемый двигателем (управляющий момент), равен Тс, а возмущающий момент — Td. Запишите уравнения, описывающие линейную модель системы, и изобразите соответствующую структурную схему.
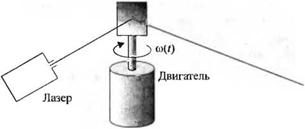
3-2.43. На рис. 2.43(3) схематически изображен оптический сканер, который часто используется для считывания штрих-кодов с товаров в супермаркетах, а также в полиграфии и ряде отраслей производства. При вращении зеркала возникает сила трения, пропорциональная угловой скорости. Коэффициент трения равен 0,06 Н • с/рад. а момент инерции — 0,1 кг • м2. Выходной переменной
является угловая скорость («(/). (а) Запишите дифферен - Рис. 2.42 (3). Ракета
циальное уравнение для двигателя, (б) Определите реак - с Двигателем с изменяемым
вектором тяги
|
Зеркало |
|
Отраженный |
|
свет |
|
|
|
|
|
Штрих-код |
|
Рис. 2.43 (3) Оптический сканер |
Детектор ^ ^ Линза
-► Микрокомпьютер
цию системы на единичное ступенчатое изменение вращающего момента, если при t = 0 начальное значение скорости равно 0,7 рад/с.
3-2.44. В поз. 10 табл. 2.5 изображен идеальный шестеренчатый редуктор. Пренебрегая моментом инерции и трением между шестернями, а также считая, что обе шестерни выполняют одинаковую работу, докажите справедливость приведённых в таблице соотношений. Определите связь между моментами Тт и TL.
|
Редуктор |
|
Двигатель |
|
Рис. 2.45 (3). Электродвигатель, редуктор и нагрузка |
|
|
3-2.45. Электродвигатель через идеальный шестеренчатый редуктор вращает массивную цилиндрическую нагрузку, как показано на рис. 2.45(3). Момент инерции вала двигателя с закрепленной на нем шестеренкой С2 равен Jm. Определите (а) момент инерции нагрузки JL и (б) момент Т на валу двигателя. Коэффициенты трения нагрузки и вала двигателя соответственно равны bL и bm.
Плотность материала диска равна р.
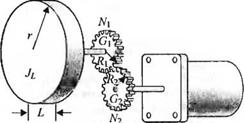
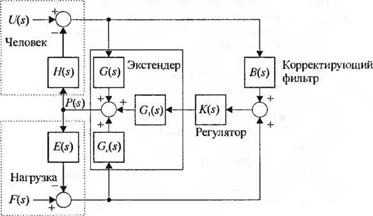
3-2.46. Робот по сравнению с человеком-операто - ром способен развивать гораздо большие усилия: в свою очередь, человек по сравнению с роботом способен совершать разумные действия. Объединение этих положительных качеств приводит к созданию класса манипуляторов, называемых экстендерами. Экстендер определяется как активный манипулятор, управляемый человеком и увеличивающий прикла-
|
|
|
Рис. 2.46 (3) Модель экстендера |
дываемые им усилия. Человек задает входное воздействие U(s), как показано на рис. 2.46(3). Выходом экстендера является P(s). Определите P(s) как функцию U(s) и F(s) в виде
P(s) = T^sjUis) + T2(s)F(s).
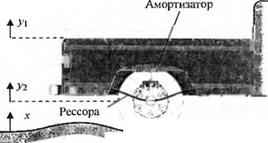
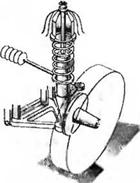
3-2.47. Груз, перевозимый автомобилем, приводит к появлению силы F. действующей на пружину амортизатора и деформирующей шину, как показано на рис.2.47(3). (а). Модель данной системы изображена на рис. 2.47(3), (б). Определите передаточную функцию )/F(s).
lr
|
Рис. 2.47 (3) Модель опоры автомобиля |
|
Сила давления груза |
|
Шина |
|
|
|
Масса автомобиля |
|
Х' |
|
Амортизатор |
|
т, |
-к, Шина
|
б) |
|
а) |
|
3-2.48. Уровень воды в баке регулируется с помощью разомкнутой системы, изображённой на рис.2.48(3). Двигатель постоянного тока, скорость вращения которого определяется током якоря ів, изменяет степень открытия вентиля. Индуктивностью якорной обмотки двигателя Lir а также коэффициентом трения при вращении его вала и вентиля, Ь, можно пренебречь. Уровень воды в баке определяется уравнением А(0= J[l,6 0(0 — Л(/)]Л. |
|
10 Ом |
|
+ V |
|
+ |
|
*„=50 |
|
<СИ |
|
Двигатель 6(f), ю(0 |
|
Усилитель |
|
Вентиль =нЫо= |
|
Рис. 2.48 (3). Разомкнутая система управления уровнем воды в баке |
|
Рис. 2.49 (3). Фильтр с опережением и отставанием по фазе |
Постоянная электродвигателя Кт = 10, а момент инерции его ротора совместно с вентилем J = 6 • 10“ кг • м". Получите дифференциальное уравнение, связывающее h(t) и v(/). а также определите передаточную функцию H(s)/V(s).
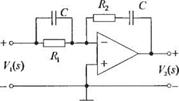
3-2.49. Схема, изображеная на рис. 2.49(3), представляет собой фильтр, обладающий как опережением, так и отставанием по фазе.
(а) Определите передаточную функцию V2(s)/Vl(s). считая, что операционный усилитель является идеальным.
|
1 мкФ и С, = 0,1 мкФ. |
|
6205 |
|
О |
|
s(s + 13s + 1281) |
|
14000 |
|
о |
|
ОД |
|
-+ Y(s) |
|
s3+45s2+3100s + 500 |
|
Рис. 2.51 (3) |
|
(б) Вычислите VjisyV^s), если Rt = 100 кОм, R2 = 200 кОм, С, (в) Разложите выражение V2(s)IVx(s) на элементарные дроби. 3-2.50. На рис. 2.50(3) изображена замкнутая система управления. R(s)- (а) Определите передаточную функцию T(s) = Y(s)/R(s). (б) Вычислите полюсы функции T(s). (в) Считая, что входной сигнал есть Рис. 2.50 (3) единичная ступенчатая функция, т. е. R{s) = 1/s, разложите Y(s) на элементарные дроби с помощью вычетов. (г) Постройте график y(t) и проанализируйте влияние вещественного и комплексных полюсов T(s). Какие полюсы — вещественный или комплексные оказывают преобладающее влияние на вид Я0? 3-2.51. На рис. 2.51(3) изображена замкнутая система управления. (а) Определите передаточную функцию T(s) = Y(s)/R(s). (б) Вычислите полюсы функции T(s). (в) Считая, что входной сигнал есть единичная ступенчатая функция, т. е. |
|
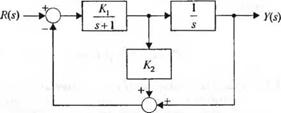
Задачи повышенной сложности П-2.1. Электродвигатель постоянного тока, управляемый по цепи якоря, приводит во вращение нагрузку. Входное напряжение равно 5 В. Спустя 2 секунды после включения двигателя его скорость равна 30 рад/с, а ее установившееся значение (при t —» °о) составляет 70 рад/с. Определите передаточную функцию (i)(s)/K(s). 11-2.2. На рис. 2.2(П) изображен сигнальный граф системы. Определите передаточную функцию T(s) = Y'oisyR^s). Желательно, чтобы >2(s) не зависело ot/?|(s) , т. е. чтобы T(s) = 0. Найдите зависимость C5(s) от остальных G,(s), при которой будет выполняться данное условие. Рис. 2.2 (П) - НА*) |
|
R(s) = І/s, разложите 7(s) на элементарные дроби с помощью вычетов. (г) Постройте график y(t) и проанализируйте влияние вещественного и комлексных полюсов T(s). Какие полюсы — вещественный или комплексные оказывают преобладающее влияние на вид Я0? (д) Предскажите конечное значение y(t) в случае единичного ступенчатого входного воздействия. |
|
|
|
Электродвигатель и вращающийся барабан |
|
|
|
ТГ Скользящая часть |
|
(б) |
|
V&)- |
|
G(s) |
|
Рис. 2.1 (СС). (а) Электродвигатель, барабан и скользящая часть стола. (б) Модель в виде структурной схемы |
|
Задачи на синтез систем СС-2.1. Перед нами поставлена задача: ^обеспечить точное позициони- Преобразование угла поворота параметры, приведенные в табл. 2.1(СС). В приводе применен двигатель постоянного тока, Таблица 2.1 (СС). Типичные параметры двигателя с управлением |
|
М. Мь г К кт Кь Яш Lm |
Масса скользящей части Масса рейки
Момент инерции барабана, якоря электродвигателя и тахогенератора Радиус барабана
Коэффициент демпфирования двигателя Постоянная электодвигателя Коэффициент противоЭДС Сопротивление якоря Индуктивность якоря____________________________________ 5,693 кг 6,96 кг
10,91 • ИГ3 кг • м2
31,75- 10“3 м 0,268 Нм- с/рад 0,8379 Н - м/А 0,838 В • с/рад 1,36 Ом
3,6 мГн_________
|
Рис. 2.1 (С). К выбору передаточных функций |
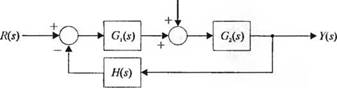
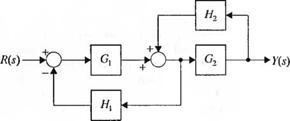
С-2.1. На рис. 2.1(C) изображена структурная схема системы управления. Передаточные функции G2(s) и Н2(s) заданы. Определите, как надо выбрать Gj(s) и Я, (у), чтобы передаточная функция замкнутой системы Y(s)/R(s) была равна единице.
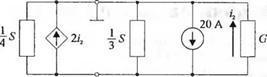
С-2.2. На рис.2.2(С) изображена схема управления лучом кинескопа. Выберите неизвестную проводимость С так, чтобы напряжение v было равно 24 В. Каждая проводимость измеряется в сименсах (5).
|
|
|
Рис. 2.2 (С). Схема управления лучом кинескопа
|
С-2.3. На вход «черного ящика» с передаточной функцией G{s) подан сигнал r(t) = t, t > 0 . При нулевых начальных условиях выходной сигнал описывается выражением
у(1) = 1 + sin / + 2ё~2' ,(>().
Определите передаточную функцию G(s).
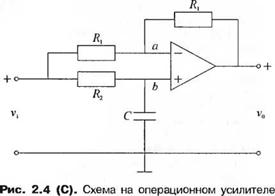
С-2.4. На рис. 2.4(C) изображена схема на операционном усилителе, которая может выполнять функции фильтра. Определите передаточную функцию схемы, считая операционный усилитель идеальным. Найдите v(j(t), если Vj(0 = At, t > 0.
{Задачи, решаемые с помощью MATLAB
М-2.1. Рассмотрите два полинома:
p(s) = s2 + 2s + 1. q(s) = s + 1.
С помощью MATLAB вычислите следующее:
Ф)
|
(в) Д-1). |
(a) p(s)q(s), (б) полюсы и нули G(s) =
/'О)
|
Рис. 2.2 (М). Система с отрицательной обратной связью |
М-2.2. Рассмотрите систему с обратной связью, изображенную на рис. 2.2(М). .
(а) Вычислите передаточную функцию * замкнутой системы с помощью функций MATLAB series и feedback.
(б) Определите реакцию системы на единичное ступенчатое воздействие с помощью функции step и убедитесь, что конечное значение выходной переменной равно 2/5.
|
Регулятор |
Объект |
|
|
1 S + 1 |
S + 2 s + 3 |
|
М-2.3. Дано дифференциальное уравнение у + 4 у + 4у= и, где >{0) = j(0) = 0 и u(t) есть единичная ступенчатая функция. Получите решение этого уравнения аналитически и проверьте результат с помощью MATLAB, одновременно построив график y(t) с помощью функции step.
М-2.4. Рассмотрите механическую систему, изображенную на рис. 2.4(М), где входом является jit). а выходом —y(t). Определите передаточную функцию, связывающую Д/) и у(/), а также с помощью MATLAB получите график реакции системы на единичное ступенчатое воздействие. Параметры системы: т = 10, к = 1 и b = 0,5. Убедитесь, что максимальное значение выходной переменной равно 1.8.
|
_____________ Коэффициент жесткости пружины к |
|
Перемещение 1 массы >'(0 |
|
|
Рис. 2.4 (М)
Механическая система «масса-пружина» с демпфированием
Коэффициент трения
ь
^■Ст1«ншмміиіииаг»ціі ■
|
Регулятор k{s + а) s + b |
|
t> |
|
Рис. 2.5 (М) Структурная схема системы управления положением спутника по одной координате |
|
ЧП —• Заданное положение |
|
Модель вращения спутника |
|
—► 6(0 Действительное положение |
М-2.5. Система управления положением спутника по'одной координате может быть представлена структурной схемой, изображенной на рис. 2.5(М). Переменные к, анЬ являются параметрами регулятора, a J есть момент инерции спутника. Примите следующие значения: J = 10.8Е+08. к= 10.8Е+08, а = 1 и Ь = 8.
(а) Напишите программу MATLAB, вычисляющую передаточную функцию замкнутой системы T(s) = 0(s)/0/s).
(б) Вычислите и постройте график реакции системы на ступенчатое изменение входного сигнала величиной 10°.
(в) Точное значение момента инерции спутника в общем случае неизвестно и может медленно изменяться во времени. Сравните реакции системы в случаях, когда J уменьшается на 20% и на 50%. Параметры регулятора при этом остаются неизменными. Проанализируйте полученные результаты.
М-2.6. Рассмотрите структурную схему системы, представленную на рис. 2.6(М).
(а) С помощью MATLAB упростите структурную схему и определите передаточную функцию замкнутой системы.
(б) С помощью функции pzmap определите положение полюсов и нулей передаточной функции замкнутой системы.
(в) С помощью функций pole и zero вычислите точные значения полюсов и нулей передаточной функции замкнутой системы и сравните результат с данными, полученными в п. (б).
|
Рис. 2.6 (М). Структурная схема многоконтурной системы управления |
М-2.7. Связь между выходом у(() и входом х(/) нелинейной системы определяется уравнением
у(х) = X2 + xsiru.
Линейная аппроксимация этой зависимости имеет вид:
у - ах,
где а — коэффициент, подлежащий определению. Определите параметр а экспериментально, разработав программу MATLAB, которая вычисляет и строит график разности между у и у в зависимости от переменного параметра а. Параметр а подбирайте так, чтобы максимальная разность между у и у не превышала значения 20 при 0 < х < 10. Когда будет найдено соответствующее значение а, постройте графики у(х) и J(x) в диапазоне 0 < х < 10.
М-2.8. Система имеет передаточную функцию
X(s)_ (15/z)(s + z)
R(s) ~ /+ 3s+15'
Постройте график реакции системы на сигнал r(t) в виде единичной ступенчатой функции при значениях параметра z = 3, 6 и 12.
Ключевые термины и понятия
Затухающие колебания. Колебания, характеризующиеся убыванием амплитуды во времени.
Имитационное моделирование. Эксперимент, при котором исследуется поведение математической модели системы в условиях реальных входных сигналов.
Исполнительное устройство. Устройство, осуществляющее непосредственное воздействие на объект управления с целью обеспечения заданного значения его выходной переменной.
Коэффициент затухания. Безразмерный параметр, входящий в характеристическое уравнение второго порядка и определяющий степень затухания.
Критическое демпфирование. Случай, которому соответствует граница между недодемпфирова - нием и передемпфированием системы.
Линейная аппроксимация. Приближенное представление модели физического устройства в виде линейной зависимости между его входной и выходной переменными.
Линейная система. Система, удовлетворяющая условиям суперпозиции и гомогенности.
Математическая модель. Описание поведения системы математическими средствами.
Передаточная функция. Отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при нулевых начальных условиях.
Правило Мейсона. Правило, позволяющее получать передаточную функцию, прослеживая пути и контуры распространения сигналов внутри системы.
Преобразование Лапласа. Преобразование функции времени Д/) в функцию комплексной переменной F(s).
Сигнальный граф. Графическое представление системы линейных уравнений, состояшее из узлов, соединённых направленными ветвями.
Структурная схема. Конфигурация системы управления, образованная совокупностью блоков однонаправленного действия, каждому из которых соответствует определенная передаточная функция.
Характеристическое уравнение. Уравнение, получающееся приравниванием нулю знаменателя передаточной функции.
Электродвигатель постоянного тока. Электрическое исполнительное устройство, входным сигналом которого является напряжение.