СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Линеаризация физических систем

Подавляющее большинство физических систем являются линейными в некотором диапа­зоне изменения переменных. Однако при неограниченном возрастании этих переменных все системы в конечном счете становятся нелинейными. Например, система, образованная массой и пружиной (рис. 2.2), является линейной и описывается уравнением (2.1) лишь при условии малых отклонений y(t). Если же>>(г) будет постоянно увеличиваться, то может на­ступить чрезмерное растяжение и разрыв пружины. Поэтому вопрос о линейности и диапа­зоне применимости этого понятия должен решаться индивидуально для каждой конкрет­ной системы.

Систему можно определить как линейную, если воспользоваться действующим на нее возмущением и реакцией на это возмущение. В случае рассмотренной выше электри­ческой цепи возмущением является входной ток r{t), а реакцией — напряжение v(0- В об­щем случае необходимым условием линейности системы является соответствующая связь между возмущением x(t) и реакцией у(1). Если к системе, находящейся в состоянии покоя, приложить возмущение xx(t), то на выходе появится реакция yt (г). Если при тех же условиях подвергнуть систему возмущению x2(t), то она даст соответствующую реакцию y2(t). Необходимым условием линейности является то, чтобы при возмущении Х|(0 + Х2(0 система давала реакцию^(f) +y2(t). Это положение обычно называют принципом супер­позиции.

Кроме того, в линейной системе должен выполняться фактор масштабирования. Опять-таки будем считать, что входом системы является переменная х, а выходом — пе­ременная >>. Тогда необходимо, чтобы при умножении входной переменной на константу

Р реакция (выходная переменная) системы изменилась в такое же число раз, т. е. оказа­лась равна Р)'. Это свойство носит название гомогенности.

Линейная система удовлетворяет свойствам суперпозиции и гомогенности.

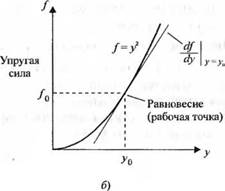
Если система характеризуется зависимостью у = х2, то она не является линейной, т. к. для нее не выполняется принцип суперпозиции. Система с уравнением >> = тх + b также не является линейной, поскольку она не обладает свойством гомогенности. Однако послед­нюю систему можно считать линейной в окрестности рабочей точки х0, у0 относительно малых приращений Дх и Ду. Если х = х0 + Ах иу = у0 + Ау, то мы получим

у = тх + Ъ,

или

j>0 + Ay = тх0 + тАх + b

и, следовательно, Ау = тАх, что удовлетворяет необходимым условиям.

Многие механические и электрические элементы в достаточно широком диапазоне изменения переменных можно считать линейными. Этого нельзя сказать о тепловых и гидравлических элементах, которые чаще всего по принципу своего действия оказывают­ся нелинейными. Однако к счастью нелинейные элементы часто удается линеаризовать при условии малых отклонений сигналов от их стационарных значений. Такой прием обычно используется для получения линейных моделей транзисторов и электронных схем. Рассмотрим общий случай, когда некоторый элемент характеризуется возмущени­ем (сквозной переменной) х(/) и реакцией на него (относительной переменной) ^(г)- Неко­торые примеры динамических систем с такими переменными приведены в табл. 2.1. Связь между переменными определяется уравнением

Л 0 = gWO], (2-6)

где #[х(/)] показывает, что_>'(/) является функцией x(t). Обозначим координату рабочей точ­ки через х0. Непрерывную функцию в окрестности рабочей точки можно разложить в ряд Тейлора:

Значение производной:

dgi dx 1*=*

характеризует наклон касательной к кривой функции^=g(x) в рабочей точке х0. Эта касате­льная может служить хорошей аппроксимацией исходной кривой в случае малых значений (х -х0), т. е. отклонения от рабочей точки. В таком предположении можно записать:

y = g(xo)+4tLv (х-х0) = у0 +т(х-х0), (2.8)

dx |x-v"

где т есть тангенс угла наклона касательной к кривой в рабочей точке. Окончательно урав­нение (2.8) можно записать в виде

(у-Уо) = т(х - х0),

или

Ау = тАх. (2.9)

Рассмотрим случай, когда груз массы М расположен на нелинейной пружине, как по­казано на рис. 2.5(a). Рабочая точка имеет место в положении равновесия, когда упругая сила пружины равна весу груза Mg, где g — ускорение силы тяжести. Таким образом, /о = Mg, как показано на рис.2.5 (б). Если нелинейная пружина характеризуется зависимо­стью/ = у2, то в положении равновесия у0 =Л1 Mg. Для малых отклонений линейная мо­дель описывается уравнением

А/ = т Ау,

где

#1

т - —

dy u

как показано на рис. 2.5(6). Следовательно, т = 2у0. Данную линейную аппроксимацию можно считать точной, поскольку допущение о малости приращений переменных полно­стью применимо к этой механической системе.

Если переменная у зависит от нескольких возмущений х,, х2,..., х,„ то функциональ­ная зависимость имеет вид:

y = g(x„х2,(2.10)

К нелинейной функции нескольких переменных также можно применить разложение в ряд Тейлора в окрестности рабочей точки с координатами лг10, х20, —, хпй. Пренебрегая членами высшего порядка малости, линейную аппроксимацию можно представить в виде:

где х0 — рабочая точка. Ниже приводится пример, иллюстрирующий применение метода линеаризации.

Пример 2.1. Модель маятника

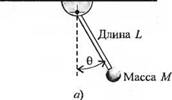
Рассмотрим колебания маятника, изображенного на рис. 2.6(a). Момент, действующий на мас­су, равен:

T=MgLsinQ, (2.12)

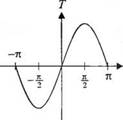
где g — ускорение силы тяжести. Условие равновесия маятника соответствует значению 0О = 0е. Нелинейная зависимость между Т и 0 графически представлена на рис. 2.6(6). Вычис­ление первой производной в точке равновесия дает линейную аппроксимацию уравнения (2.12), которая имеет вид:

{в-еьх

(Ю *

0. Следовательно, мы имеем:

Т = MgL(cosO°)(0 - 0°) = MgLQ. (2.13)

Подобная аппроксимация является достаточно приемлемой в диапазоне - л/4 < 0 < л/4. Напри­мер, колебания линейной модели в диапазоне +30° от положения равновесия отличаются всего на 2% от действительных колебаний маятника.

Рис. 2.6

Колебания маятника

2.4. Преобразование Лапласа

Возможность линеаризации физических систем предоставляет в распоряжение ис­следователя аппарат преобразования Лапласа. Метод преобразования Лапласа позволя­ет заменить достаточно сложное решение дифференциальных уравнений относительно простым решением алгебраических уравнений. Определение реакции системы на входное воздействие подразумевает следующие действия:

1. Получение дифференциальных уравнений.

2. Преобразование по Лапласу этих дифференциальных уравнений.

3. Решение полученных алгебраических уравнений относительно переменной, пред­ставляющей интерес.

Для того чтобы функция/(f) имела преобразование Лапласа, достаточно, чтобы вы­полнялось условие

т. е. данный интеграл должен сходиться для некоторого действительного положительного а[. Если | /(0 | < Меш для всех положительных г, то интеграл будет сходиться при а [ > а. Та­ким образом, область сходимости определяется неравенством аз > > а, где а! известна

как абсцисса абсолютной сходимости. Все физически реализуемые сигналы имеют преоб­
разование Лапласа. Преобразование Лапласа функции времени fit) определяется выраже­нием

F(s)= f At)e-s'dt=L{f(t)}.

Обратное преобразование Лапласа имеет вид

га+/оо

/(')“[ F(s)e ds. 2л/___________

При решении большинства практических задач используются таблицы преобразо - ваний Лапласа, полученные на основании выражения (2.14). В табл. 2.3 приведены основные прямые и обратные преобразования Лапласа, а более подробную таблицу можно найти на Web-сайте MCS.

Таблица 2.3. Некоторые важные преобразования Лапласа

F(s)

Ступенчатая функция, u{t) ё~а‘ sin(tor) cos(cof)

t"

/И(0

dt

j'f№

Импульсная функция. 5(/)

e~al sin(to()

e COS(tl)f)

—[(a - a)2 + or ]2e al sin(fi)/ + ф), ф = arctg-

''sin(co„VlC< 1

- e a1 sin(ti)/ - фj, ф = arctg-

a~ + or (o-/g2+ <ii

1

Переменную j в преобразовании Лапласа можно рассматривать как оператор диффе­ренцирования, т. е.

s = —. (2.16)

Л

Аналогично можно ввести оператор интегрирования

1 г'

-=| dt. (2.17)

S J0“

Обратное преобразование Лапласа обычно находят путем разложения F{s) на про­стые дроби с помощью правила Хевисайда. Этот метод, в частности, полезен при анализе

и синтезе систем управления, т. к. он позволяет легко выявить влияние каждого корня ха­рактеристического уравнения системы.

Чтобы проиллюстрировать преимущества преобразования Лапласа, рассмотрим еще раз механическую колебательную систему, описываемую уравнением (2.1), которое име­ет вид

d2y udy

—f + 6 —

dt2 dt

Нам необходимо получить решение этого уравнения, т. е. выражениеy(t). Преобразование Лапласа уравнения (2.18) имеет вид:

Ms2Y(s) - Msy0 + bsY(s) - by0 + kY(s) = 0. (2.20)

Выражая отсюда K(.v), получим:

ns> =£M (22])

Ms~ +bs+k q(s)

Если полином cy(.v), стоящий в знаменателе, приравнять нулю, то мы получим харак­теристическое уравнение, названное так потому, что его корни определяют характер движения системы. Корни характеристического уравнения называют также полюсами системы. Корни полиномаp(s), стоящего в числителе, называют нулями системы; напри­мер, выражение (2.21) имеет нуль. v = - ЫМ. В полюсах функция Y(s) обращается в беско­нечность, а в нулях она становится равной нулю. Расположение полюсов и нулей на комп­лексной s-плоскости определяет характер собственного (свободного) движения системы.

Рассмотрим частный случай, когда к/М= 2 и ЫМ= 3. Тогда выражение (2.21) примет

вид:

Y (s) = -3-ty? . (2.22)

(s+l)(s + 2)

Положение полюсов и нуля этой функции на s-плоскости показано на рис. 2.7. Разло­жив (2.22) на элементарные дроби, получим:

к, к-.

где допускается наличие простого полюса У(л) в начале координат, но не допускается нали­чие полюсов на мнимой оси и в правой полуплоскости, а также кратных полюсов в начале координат. Следовательно, для системы масса-пружина мы получим:

lim y(t) = limsy(s) = 0, (2.29)

/ —>оо. v—>0

т. е. конечное положение массы соответствует положению равновесия}’ = 0.

Чтобы лучше продемонстрировать достоинства метода преобразования Лапласа, рас­смотрим еще раз систему масса-пружина для случая недодемпфированного движения. Выражение для Y(s) можно записать в виде:

сs+b/M)y0 (s + 2C, a„)y0

Y(s) = -

s2 +(b/M)s+(k/M) s2 +2^o)„s+o)2

где С, — безразмерный коэффициент затухания, а ю„ — собственная частота колебаний системы. Корни характеристического уравнения равны:

51-52 (2-31)

где, в нашем случае, ю„ = 4ШІ и £= Ы2-4Ш. Если С > 1 , то корни являются вещественны­ми; при С, < 1 корни являются комплексно-сопряженныМи. При С, = 1 корни являются веще­ственными и кратными, что соответствует так называемому критическому затуханию.

Если С, < 1, то реакция системы является недодемпфированной, и

л-и = - фп (2.32)

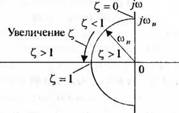
На рис. 2.9 показано расположение полюсов и нуля функции У(л), где 0 = arccos С,. При изменении С, и сохранении постоянным значения сои комплексно-сопряженные полю­сы перемещаются по окружности, как показано на рис. 2.10. Переходная характеристика все более приобретает колебательный характер по мере того, как полюсы приближаются к мнимой оси при С, -> 0.

Обратное преобразование Лапласа можно найти путем графического определения вычетов. Разложение (2.30) на элементарные дроби дает:

ki ко

У(*)=-

5-^! S-S-,

Поскольку и s2 являются комплексно-сопряженными, то вычет к2 также является комплексно-сопряженным вычету ки и мы имеем:

кх кх

П*)=-

Рис. 2.9. Расположение на s-плоскости полюсов и нуля Y[s)

Рис. 2.11

Определение вычета к-[

где звездочка обозначает комплексно-сопряженное значение. На основании рис. 2.11 вы­чет кх находится как

' (2 34)

М2Є^12

где Мх есть модуль (s, + 2£(0„), а М2 — соответственно модуль (sj — )l Основные сведения по комплексным числам и операциям с ними приведены на Web-cairre MCS. В данном случае мы получим:

£ _ Уос)пе _____________________________ (235)

' 2^,-^е^1 2A/l^V(n/2-e) ’

где 0 = arccos^. Следовательно,

k-> -—ej(jl,2~G). (2.36)

Окончательно, введя обозначение ф-С? = р, мы получим:

yit) = kxes' +к, е* = +еЛ"/2-ь)е-^п'е-лР' ) =

2л^

а

= е-'4' sin(co, lA/l-C2^ + 6) • (2.37)

1-С

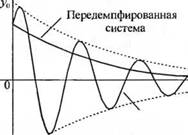
То же самое решение можно получить с помощью п. 11 таблицы 2.3. Переходные характе­ристики для случаев передемпфированной (^ > 1) и недодемпфированной (£ < 1) системы приведены на рис. 2.12. Переходной характеристике при С, < 1 свойственно уменьшение со временем амплитуды колебаний, поэтому она носит название затухающих колебаний.

Между расположением полюсов и нулей на 5-плоскости и видом переходной харак­теристики существует прямая и однозначная зависимость. В то же время степень влияния каждого полюса, представляемая соответствующим вычетом, очень легко прослеживает­ся, исходя из графического определения вычетов на ^-плоскости. Преобразование Лапла­са и использование ^-плоскости являются очень ценными методами анализа и синтеза си­стем, когда акцент делается на определение переходных режимов и точность в установив­шемся состоянии. Поскольку при исследовании систем управления в первую очередь представляют интерес именно два указанных фактора, то в связи с этим трудно переоце­нить метод преобразования Лапласа.

Рис. 2.12

Переходные

характеристики

системы

масса-пружина