ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ОПРЕДЕЛЕНИЕ ВЕКТОРА БЮРГЕРСА ЧЕРЕЗ КОНТУРНЫЙ ИНТЕГРАЛ И ВИДЫ ДИСЛОКАЦИЙ
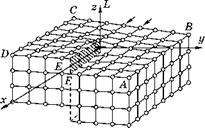
Мощность дислокации (величина несовершенства кристалла, связанная с дислокацией) определяется вектором Бюргерса b. Направим ось 2 вдоль линии дислокации L (для краевой дислокации рис. 4.2 эта линия является краем лишней плоскости, вставленной в кристалл).
Если линия дислокации изогнута, то ось 2 направляют по касательной к этой линии в рассматриваемой точке. Ось у направлена по лишней плоскости, х — перпендикулярно первым двум осям. Кристаллическая решетка на рис. 4.2 кубическая. Межатомное расстояние обозначено скалярной величиной b. Кроме того, осям х, у, 2 следует приписать орты i, j, k.
Для того, чтобы определить вектор Бюргерса, надо обойти линию дислокации на достаточно большом расстоянии и вычислить контурный интеграл, суммируя векторно межатомные расстояния. Форма контура обхода произвольна. Выбирают простейший контур — например в случае, изображенном на рис. 4.2, можно линию дислокации L обойти по прямоугольному контуру S = ABCDA. В результате подсчета межатомных промежутков получим
|
b = - |
ds =-(6j ■ b -8i ■ b -6 j ■ b + 7i ■ b) = i ■ b. (4.10)
|
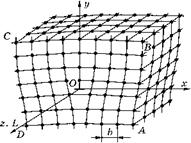
Рис. 4.3 Винтовая дислокация b = k ■ b |
|
Рис. 4.2 _ Краевая дислокация b = i ■ b |
Как видно, у краевой дислокации вектор Бюргерса направлен перпендикулярно линии дислокации и равен одному межатомному расстоянию. Это отличительная особенность краевых дислокаций.
На рис. 4.3 представлена аналогичная схема винтовой дислокации.
Оси x, y, z относительно линии дислокации расположены так же, как на рис. 4.2. Для нахождения вектора Бюргерса этой дислокации ее линию L можно обойти по контуру S = ABCDEFA. Подсчитывая межатомные промежутки на этом пути, получим
Ъ =-(|ds =-(-7i b-7j b + 7i b + 3,5j b-k b + 3,5j b) = k b. (4.11)
(S)
Как видно, у винтовой дислокации вектор Бюргерса ориентирован параллельно линии дислокации L. Это отличительная особенность винтовых дислокаций, которые можно представить как надрез ножницами части кристалла вплоть до линии дислокации L.
Точку выхода линии дислокации на поверхность чертежа обозначают знаком ±. Эти знаки поставлены на рис. 4.2 и 4.3.
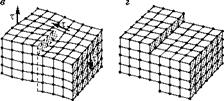
На рис. 4.4 схематически показаны результаты движения дислокаций.
Краевая дислокация (рис. 4.4а) движется в направлении приложенных касательных напряжений т. При выходе линии дислокации на правую границу кристалла там создается уступ b (рис. 4.46).
Винтовая дислокация (рис. 4.4в) движется в направлении, перпендикулярном приложенным напряжениям т. При резке листа бумаги ножницами происходит то же самое. Когда дислокация прошла через весь кристалл, на его верхней и нижней поверхностях образуется вертикальный уступ, равный вектору Бюргерса b (рис. 4.4г).
|
|
|
Рис. 4.4 Результаты движения винтовой дислокации |
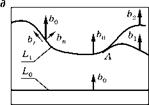
Дислокация не может ни начинаться, ни заканчиваться внутри кристалла. Ее вектор Бюргерса не меняется при движении линии дислокации. При перемещении дислокации из положения L0 в положение L1 (рис. 4.45) по всей ее длине вектор Бюргерса b0 постоянен (b2 = b1 = b0).
Если дислокация перемещается и изгибается (положение L1, рис. 4.4д), то вектор Бюргерса во всех точках ее линии остается неизменным. Однако если вектор Бюргерса оказывается под углом к линии дислокации, то его разлагают на краевую (bn) и винтовую (bt) составляющие. Дислокацию в этом месте называют смешанной.
Если дислокация разветвляется, как это показано в точке А рис. 4.4д, то векторная сумма векторов Бюргерса обеих ветвей равна вектору Бюргерса исходной дислокации: b1 + b2 = b0.
.