ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
СОПРОТИВЛЕНИЕ МЕТАЛЛА ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
4.1.
ТЕОРЕТИЧЕСКАЯ ПРОЧНОСТЬ МЕТАЛЛА НА СДВИГ
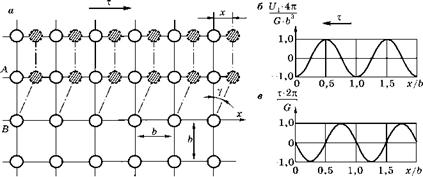
Задача о приближенной оценке величины теоретической прочности металла на сдвиг была решена в 1920-х годах на основании схемы, приведенной ниже. На рис. 4.1 схематически показана диагональная плоскость объемно центрированной кубической кристаллической решетки с межатомными расстояниями b.
Под действием касательных напряжений т верхняя часть кристалла сдвигается относительно нижней части на расстояние х (как показано заштрихованными кружками). При этом между атомными плоскостями A и B возникает сдвиговая деформация tg(y) = x/b.
Потенциальная энергия U1 (индекс 1 показывает, что эта функция относится к одному атому решетки) каждого атома слоя A относительно атомов слоя B должна изменяться с увеличением x по циклической зависимости c периодом b. Ее можно описать рядом
|
Рис. 4.1 Схема сдвига атомов в кристаллической решетке (а) и графики изменения энергии U1 (б) и касательных напряжений т (в) при смещении атома x |
Фурье. Однако в первом приближении можно ограничиться только первым членом этого ряда:
U1= A ■ sin(k • x + ф) + В, (4.1)
где A, B, k и ф — постоянные.
Для того чтобы функция U1(x) имела период b, нужно выполнение условия sin(k ■ X + ф) = sin[k ■ (x + b) + ф], или k ■ (x + b) = = k ■ x + 2л. Следовательно, k ■ b = 2л и
k = ^. (4.2)
b
Чтобы при x = 0 атомы находились в устойчивом положении, потенциальная энергия U1 должна быть минимальной. Это будет справедливо, если sin^) = -1, или
Ф = f. (4.3)
Подставив формулы (4.2) и (4.3) в формулу (4.1), для потенциальной энергии атома получим выражение
U1 = A ■ sin I2*, x + -34lJ + B = B - A ■ cosl^bj. (4.4)
График этой функции при B = 0 показан на рис. 4.16.
Найдем выражение для касательной силы T1, действующей на один атом. Когда мы гирю весом P кг поднимаем на высоту АН, мы совершаем работу AU = P ■ АН, и потенциальная энергия гири увеличивается на величину AU. Следовательно, зная приращение энергии AU, постоянную силу Р можно определять по формуле
P = au = dU
АН dh'
Переход в последнем равенстве к производной делает формулу пригодной и для вычисления переменной силы Р. Поэтому в случае формулы (4.4) силу T1, действующую на один атом, можно определить как производную от потенциальной энергии:
_ A • ¥• sin f2^). (4.5)
|
B-A•cos1 2n'x |
T d
1 dx
С другой стороны, усилие T1 можно определить как приложенные к кристаллу напряжения т, умноженные на площадь F1 атомной плоскости A, приходящуюся на один атом (F1 = b2). Приравнивая эти два значения усилия N^ получим:
A ■ -2^ sin | %*) = т ■ b2,
откуда получим выражение для напряжении:
т = A-2bf-sin (2b*). (4.6)
Неизвестную постояннуюA можно найти, используя определение модуля сдвига G.
Согласно рис. 4.1а, угол сдвига у = tg(y) = х/b; dx/dy = b. Следовательно, модуль сдвига можно выразить формулой
|
>_ lb-3, |
|
A ■ 2л 2п ( 2л - х b3 b b |
|
х —^0, |
|
G _(_dr | | _Эг_ _(Эх| _ V dy)Y^0 'Эх'х^0 V^y |
откуда
A - ^ ^
Подставив формулу (4.7) в формулу (4.6), получим выражение для касательных напряжений:
-G^^sin^i-sin^). (4.В)
График функции т(х) показан на рис. 4.1в.
Из формулы (4.В) видно, что максимальные напряжения возникают при
2ьх = Е или х = b. b 2 4
Критическая деформация ус составляет tg(yc) = х = 4 = 25%.
Следовательно, теоретическая прочность материала на сдвиг St:
G
St =Tmax. (4.9)
Для железа модуль нормальной упругости E = 2,1 • 104 кГ/мм2; модуль сдвига G = E/[2 • (1 + v)]; коэффициент Пуассона v = 0,3. В результате получим
St = E = тЕт = 12В5 Кг/мм2
t 2л-2(1 + v) 16,3 '
В литературе приводятся экспериментальные значения прочности усов железа диаметром 1,6 мкм. Критические напряжения растяжения для них Sn = 1340 кГ/мм2 и критические напряжения сдвига при течении St = 364 кГ/мм2. Последнее значение в 3,5 раза меньше, чем вычислено по формуле (4.9).
Конечно, выполненное здесь определение теоретической прочности на сдвиг очень грубо, так как учтен только один член раз-
ложения 171 в ряд Фурье. Оно вполне может давать ошибку в 23 раза. Но следует учитывать, что нагрузить ус диаметром 1,6 мкм равномерно при испытаниях на срез практически невозможно. Коэффициент концентрации т при таких испытаниях вполне мог достигать 3, и этим можно объяснить заниженное значение экспериментальной прочности усов железа при сдвиге.
На основании изложенного выше можно утверждать, что для сдвига атомов железа друг относительно друга в металле нужно создать локальные напряжения сдвига в несколько сотен кГ/мм2. Такие напряжения в десятки раз превышают наблюдаемые значения предела текучести на срез. Следовательно, при пластической деформации металла должен существовать механизм, который концентрирует приложенные сдвиговые напряжения в десятки раз. Такой механизм создают дислокации.