Выравнивание начального распределения температуры
|
|
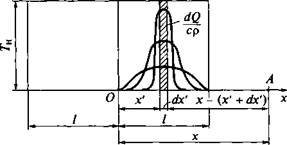
Начальное распределение температуры Т(х, у, z, 0), заданное начальными условиями задачи, можно рассматривать как результат действия совокупности мгновенных источников теплоты, распределенных соответствующим образом по объему тела. Рассмотрим в качестве примера выравнивание температур в бесконечном стержне сечением F, который при t = 0 был нагрет до Гн на участке длиной 21; будем полагать, что остальная часть стержня имеет нулевую температуру (рис. 6.6, 6.7). Выделим некоторый элементарный слой с координатой х' и толщиной dx в котором при t - 0 сосредоточено количество теплоты dQ = cpTHFdxr. Будем рассматривать его как мгновенный плоский источник теплоты. Приращение температуры от действия данного источника в сечении А, имеющем произвольную координату х, составит
(6.10)
т
|
Рис. 6.6. Схема представления начального распределения температуры Тн на участке 21 в стержне совокупностью мгновенных плоских источников теплоты |
|
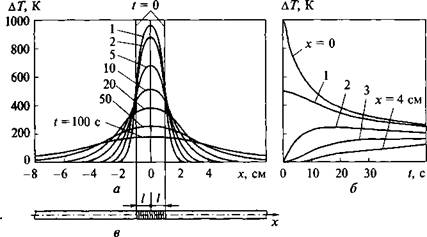
Рис. 6.7. Процесс выравнивания температуры в неограниченном стержне, участок которого 21 = 2 см был нагрет при / = 0 до Тн = 1000 К (а = 0,1 см2/с): а - распределения температуры в различные моменты времени; б - термические циклы в различных сечениях; в - схема стержня |
Полное изменение температуры в сечении А определяется интегрированием приращений температур от совокупности элементарных источников теплоты, расположенных на участке [-/, + /], т. е.
|
ТА=1 |
|
dx'. |
|
(6.11) |
|
exp |
|
4 at |
|
срТ» j cpl4nat |
|
Для вычисления интеграла (6.11) применим подстановку |
|
(х-х) , dx' и -—г—аи =— |
|
^4аї |
|
и с учетом смены пределов интегрирования получим Х+І т„ 2 ^ _„2 , г |
|
ТА=2L-== f е~ы du=^- Л 2 Л J, 2 |
|
f I У X-I |
|
jAat |
|
х + 1л |
|
-ф |
|
(6.12) |
|
Ф |
|
yjAat J 4Aat |
Выражение (6.12) описывает процесс выравнивания температуры. Температура середины нагретого участка остается наиболее высокой температурой в стержне за все время процесса выравнивания (см. рис. 6.7).