Мгновенный точечный источник в бесконечном теле
В начальный момент времени t = 0 в бесконечно малом элементе объема dxdydz неограниченного теплопроводящего тела с
|
|
равномерно распределенной начальной температурой Тн сосредоточено количество теплоты 0. Тогда в прямоугольной декартовой системе координат Oxyz, начало которой О совпадает с точкой сосредоточения теплоты (см. рис. 5.5, а), нестационарное температурное поле от действия мгновенного точечного источника теплоты описывается выражением
|
где R = yf. |
'2 2 2
х + у + z - расстояние от источника теплоты до точки
тела с координатами jc, у, z; t - время, отсчитываемое от момента ввода теплоты; АТ - изменение температуры в произвольной точке тела с координатами х, у, z в момент времени /. Выражение
(6.1) является решением дифференциального уравнения теплопроводности (5.22). Очевидно, что температурное поле в данном случае симметрично относительно точки О, термический цикл любой точки тела определяется только модулем ее радиус-вектора Л, а изотермическими поверхностями являются концентрические сферы R = const с центром в точке О.
|
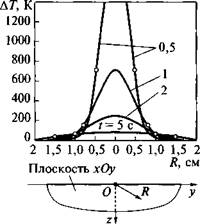
Рис. 6.1. Распределение приращения температуры АТ по расстоянию R от мгновенного точечного источника теплоты в полубесконечном теле (Q = 2 кДж, ср = 4 Дж/(см3 • К), а = 0,1 см2/с) в различные моменты времени |
В начальный момент времени / = 0 выражение (6.1) дает бесконечно большую температуру в точке О, так как в этот момент времени конечное количество теплоты сосредоточено в бесконечно малом объеме источника (точке О). Во всем объеме тела вне источника температура равна начальной:
в начальный момент времени
По мере того как теплота источника распространяется по телу, температуры отдельных точек тела меняются (рис. 6.1), но общее теплосодержание остается постоянным, так как бесконечное тело не теряет теплоту в окружающую среду. В весьма удаленных от источника точках температура во все время процесса не изменяется Г(оо, t) = Гн.