Оптоэлектроника

Электролюминесценция

При появлении избыточных носителей в области перехода, они распределяются по зоне проводимости и валентной зоне, занимая все более высокие энергетические уровни (смотрите рис. 13.3). При использовании модели с единственной валентной подзоной распределения носителей могут быть записаны с использованием квази­уровней Ферми (смотрите раздел 7.6) ЕРс (для электронов в зоне проводимости) и Е (в валентной зоне):

Ег + кТЕ

(13.4)

-

Еу кТР|/2

Здесь Е1/2 есть величина, обратная интегралу Ферми—Дирака Е1/2, определяемому

Формулой:

-1/2

(13.5)

Как это уже обсуждалось в разделе 7.4, это отклонение от равновесия, описыва­емое квазиуровнями Ферми для электронов и дырок, вызывает усиление спонтан­ной эмиссиии со спектральным распределением скорости К5роп(Ьу) в единицу вре­мени в единичном объеме и энергетическом интервале (для фотонов с энергией Иу), описываемым (7.47):

Рис. 13.3. Оптические переходы в по­лупроводнике являются вертикальными (т. е. с сохранением к) по энергии. Со­стояния Ес(Иу) и Еу{Иу) соединены друг с другом оптическими переходами с учас­тием фотонов с энергией Л к СВ-зона проводимости, УВ-валентная зона.

Л*ро„ (М= — (л V V; (л V X? - л(М]

Для величин, появляющихся в этом выражения мы еще раз напоминаем их опреде­ления, приведенные в главе 6:

• гя есть спонтанное излучательное время жизни в излучающем материале, которое можно предполагать относительно не зависящим от энергии излучаемых фото­нов. Эта величина является характеристикой данного материала, и она зависит от физических параметров этого материала (эффективных масс носителей, матрич­ных элементов Кейна и т. д.), как это описывается (7.37б).

• /?.(/* V) есть комбинированная плотность состояний (7.19). Этот параметр учитывает число состояний, удовлетворяющих требованиям сохранения энергии Ну = Ес(к) — Еу(к) и квазиимпульса (постоянное значение к) для переходов между состояниями с энер­гией £(к) в валентной зоне и Ес(к) в зоне проводимости (смотрите рис. 13.3).

•/с и/у(Иу) есть функции Ферми—Дирака, описывающие заселенность состоя­ний, связанных оптическими переходами, т. е. удовлетворяющих (7.255, в):

1

ЕГс

КТ

(13.7а)

Ес(/гу)=Ее+ЩИу-Ее)

/я.

ЕЛИу)-Ег,

КТ

Ef(hv)=-?t(hv-Eg)

Как правило, в случае электролюминесцентных диодов концентрация избыточ­ных носителей достаточна мала, что оправдывает аппроксимацию функций Фер­ми-Дирака функциями Больцмана, что соответствует тому, что квазиуровни Фер­ми далеки от экстремумов зон. Как было показано в главе 7, в этом случае спект­ральная зависимость скорости спонтанной эмиссии может быть существенно упрощена, что дает (смотрите 7.52а):

Здесь Kspon определяется формулой:

(13.9)

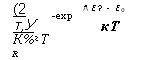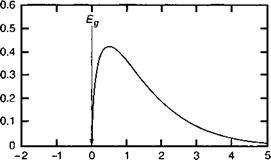
При этом АЕр есть энергетический зазор между квазиуровнями Ферми AEF = EFc — EFv. Очевидно, что по мере возрастания концентрации избыточных носителей п множи­тели exp (EJkT) и exp (—EJkT) также возрастают, приводя к тому, что спектраль­ная зависимость скорости Rspon(hv) пропорциональна я2, что и неудивительно. Фор­ма спектральной линии спонтанной эмиссии определяется (13.8). Тривиальным образом можно показать, что максимальная интенсивность излучения достигается при hvpcak = Eg + АТ/2, при этом полуширина линии составляет A hv~ 1,8 кТ (смотри­те рис. 13.4).

Поскольку Лрсак и hvptak связаны соотношением Лреак(мкм) = l,24//zvpeak (эВ), мы сразу находим, что на шкале длин волн полуширина А Л связана с пиковой длиной волны следующим выражением:

АЛ = 1,45 Л^кТ

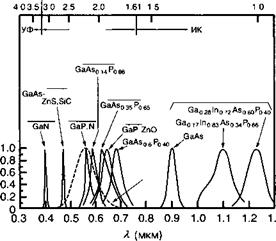
На рисунке 13.5 представлены спектральные распределения плотности излуче­ния СИД, изготовленных на основе различных полупроводников. Как и предска­зывается формулой (13.10), спектры излучения становятся уже (на шкале длин волн) по мере изменения энергии излучения от инфракрасного к ультрафиолетовому ди­апазону спектра.