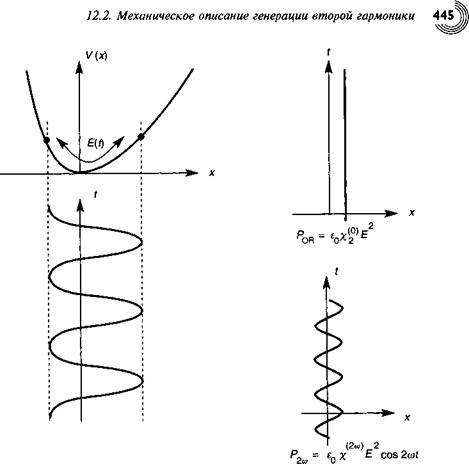
Механическое описание генерации второй гармоники
Как мы теперь уже знаем, механическая модель упруго связанного электрона успешно описывает ряд оптических эффектов таких, как спектральную дисперсию (дополнение 7.Б). Сейчас же мы попробуем установить поведение электрона, подверженного воздействию ограничивающего потенциала, содержащего неквадратичные члены более высокого порядка. Для упрощения предположим, что ограничивающий потенциал и(х) является одномерным, при этом он может быть записан в виде (смотрите рисунок 12.1):
И(х)- ^тсох2 + —/и/)*3 (12.1)
Здесь о)0 есть собственная частота колебаний осциллятора в линейном режиме, т - масса электрона в вакууме, а />есть коэффициент нелинейности (в единицах м-1 с"2). Эта система подвергается воздействию дипольной электродвижущей силы:
|
Рис. 12.1. Электрон, ограниченный асимметричным потенциалом и возбуждаемый электромагнитным полем Е соscot (а), испытывает ангармонические колебания около своей точки равновесия (б). Его движение содержит постоянную компоненту (в) и компоненту при 2(0 (г), которые порождают соответственно постоянную поляризацию (оптическое выпрямление) и генерацию сигнала второй гармоники. |
Как обычно, здесь к. с. означает комплексно сопряженную величину. Таким образом, движение частицы х(/) подчиняется следующему дифференциальному уравнению:
Х + }х + а%х + £)х2 = ~~~ + к. с.) (12.3)
2т
Здесь: у есть коэффициент трения частицы, который определяет ширину соответствующего оптического перехода (смотрите дополнение З. А). Поскольку, очевидно, что движение частицы должно быть периодическим (с частотой со и ее соответствующими гармониками), то мы можем провести гармонический анализ х(/), записав этот параметр в виде:
*(0=-|(*о+ V" +х2е‘2м + ...+ К. С.) (12.4)
Временно предположим, что х0 = 0, т. е., что в системе отсутствует постоянная наведенная поляризация. Однако позже мы увидим, что соответствующий член может существовать, что приводит к эффекту оптического выпрямления. Подставляя (12.4) в (12.3), получаем:
2
--у-(jc1eIfflr + к. с.)- 2о?(х2е12<а + к. с.)+^~(х^ш + к. с.)+ icoy(x2el2a* + к. с.)+
+ + к. с.)+ - у - (x2ti2°* + к. с.)+ ^ (х2е2Ш + 2х1х2еш + (12.5)
+ jc, jc* + х2х* + 2х1х2еУ1й* + х2е4'“* + к. c.)=f(e - + к. с.)
На первый взгляд эта формула может показаться сложной, но, как это часто имеет место в нелинейной оптике, она может быть существенно упрощена за счет группировки подобных членов.
Сначала мы рассмотрим линейный отклик, т. е. члены при е1й", и пренебрежем ими в D. При этом для со - со0 мы сразу находим:
Х _ яЕ ' 1 дЕ_____ 1 ,126ч
1 Т щ - со2)+(оу 2сот (со0 - со)+у / 2
Движение, описываемое соотношением *,(/) = х^ш + к. с., приводит к линейной поляризации среды:
/?(*) = Nqx](t)= Nqxfe'“* + к. с.) (12.7)
Где N есть объемная плотность систем, взаимодействующих с волной. В этом случае мы можем провести идентификацию каждого члена в выражении (12.7) для линейной восприимчивости, приведенной в (3.24):
Ж^уСгГ^ + к. с.) (12.8)
Это приводит к следующему выражению:
Х<(®> = N<*2______ ______ (12.9)
1 2оте0 (щ - w)+iy/ 2
Этот последний результат эквивалентен тому, который получается в классической модели Лоренца в рамках квантовой механики, рассмотренной в главах 2 и 3. Используя в наших рассуждениях метод индукции, мы определим нелинейную восприимчивость второго рода как:
^(0= |Ыэд£2е‘2" + К. с.)= ^-{х2с2М + к. с.) (12.10)
Член с х2 обусловлен нелинейным квадратичным членом Dx2 в (12.3). Его выражение может быть получено из (12.5) из идентификации членов при e2i6":
Х2(-4 со2 + 2i Gyy + col)= ~^Dx2 (12.11а)
Из последнего выражения мы видим, что именно член х2 обусловливает движение электрона с частотой 2со. Используя (12.6), мы находим:
*2 = ________________________ !_______________ Е> т
2mi [(<у02 - <»2)+ icorY!L<»l ~ 4ю2)+ 2io)y]
..I’D > .£,
24т2соъ [(«о - (о)+ у /2]2[Оо0 -2©)+(2/3)!у]
После подстановки этого последнего уравнения в (12.10) мы можем найти восприимчивость второго порядка в виде:
=__ МП___________________ !_____________ (12Л2)
24е0т2о)1 [(а>0 - а)+ ^/2]2[(<»0 - 2а)+ (2/3)1у]
В этом месте несколько моментов заслуживает упоминания. Во-первых, система является дважды резонансной при со = а)0 и при со = 2со0. В дополнение к этому из сравнения (12.12) и (12.9) мы видим, что эта модель предсказывает следующую связь между линейной и нелинейной восприимчивостью:
У уп Г)
------ &--------- = ти - = 8™ (12.13)
(х^У Х2“)£о 2ЛГ»*>
Как следует из (12.13) параметр д{2т) (называемый параметром Миллера) должен быть аналогичен во всех материалах, что в значительной степени имеет место. В таблице 12.1 представлены значения нелинейной восприимчивости второго рода для различных полупроводников. Взглянув на эту таблицу, мы отмечаем, что 8™ * 3 - 8 х 109 Б!.
|
Таблица 12.1. Коэффициенты оптического преломления на фундаментальной длине волны 10,6 мкм п2т, на частоте второй гармоники 5,3 мкм, квадратичная восприимчивость %2 и параметры Миллера для ряда полупроводников (значения п1о) и £МШег для 1п8Ь не определены)
|
Теперь сконструируем чрезвычайно грубую модель для несимметричного кристалла, которая позволит нам получить величину Д исходя из фундаментальных констант. Для этого предположим, что электроны в таком кристалле подвержены воздействию притягивающего потенциала, обусловленного ядром с зарядом 2# и вторым ядром с зарядом #, удаленным на расстояние а от первого ядра. Этот потенциал может быть записан в виде:
|
1 |
|
К(х)=- |
|
Вблизи минимума этот потенциал может быть разложен в ряд: |
|
|
4 яеп |
|
1 2 — +------ Х а-х |
|
4 ЛЕ0Д |
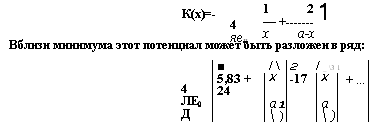 |
|
|
|
|
|
В этом случае коэффициент нелинейности в (12.1) получается отождествлением подобных членов, что дает:
Полагая, что типичное межатомное расстояние а составляет 5 А, мы находим, что В= 2 х 1041 м-1 с-2, а это приводит к параметру Миллера &2со) величиной 6 х 109 Б1 для концентрации N атомов величиной 6 х 1028 атомов/м3 (смотрите уравнение (12.13)). Наша простая модель, приписывающая природу оптической нелинейности в материале асимметрии атомных потенциалов, образующих среду атомов, приводит к результатам, согласующимся с экспериментально определенными величинами. В дополнении 12.А мы представляем более последовательный квантово-механический вывод, основанный на формализме матрицы плотности.
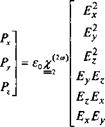 Наконец, очевидным является то, что величина %2 по своей природе является тензором. Если фундаментальная волна обладает компонентами (Ех, Е, £), волна второй гармоники будет обладать компонентами (Рх, Р, Р), которые, в (юлее общем случае, будут определяться квадратичными комбинациями компонент Ех, Еу и £, а именно:
Наконец, очевидным является то, что величина %2 по своей природе является тензором. Если фундаментальная волна обладает компонентами (Ех, Е, £), волна второй гармоники будет обладать компонентами (Рх, Р, Р), которые, в (юлее общем случае, будут определяться квадратичными комбинациями компонент Ех, Еу и £, а именно:
(12.17)
Тензоры %(2а}) обладают свойствами, которые сильно зависят от симметрии рассматриваемого кристалла. Сейчас мы не будем вдаваться в подробности классификации этих различных типов симметрии, а ограничимся описанием различных оптоэлектронных приборов, использующих нелинейные свойства этих материалов.