Шум умножения
В разделе 11.7 мы видели, каким образом генерационный шум в лавинных диодах умножается за счет ударной ионизации. Поскольку генерационный ток также является источником шума, мы можем ожидать, что этот шум должен усиливаться при лавинном умножении. Однако, процесс ударной ионизации является также и случайным процессом и дает свой вклад в полный шум. Для описания шума в лавинном приемнике излучения нам необходимо обобщить уравнения раздела 11.7 с тем, чтобы мы могли найти ток 1(х0), обусловленный источником генерационного шума дСА&хд (х — х0), расположенного при я: = х0, 0 < х0 < Ь. В этом случае уравнение (11.70) может быть записано в виде:
= а„1„ + ар1р + дСААхб(х - х0)
(11.А.46)
- = А„1„ + «,/, + дСААхд(х - х0)
При этом граничные условия имеют вид /(0) = /(/,) = 0. Для полного тока 1(х0) решение для /, использующее эти граничные условия, имеет вид:
An[22]Ixo)^ _ е_Д(И^ о < х < х0
|
Г,(Х’ *») = |
- к х0<х< L
<х„-ар
Здесь: Аа= а (1 — к) = а — а и к = а /а.
П' ' п р р' п
При х = х0 интегрированием (11.А.46) вблизи х = х0 мы получаем:
1„ («о; *0)- Jp (*о; *о)= qGAAx (11 - А.48)
Это позволяет нам определить 1(х0):
I(x0)= qGAAx АаеАт' = qGAAxM (х0) (11.А.49)
Ап - a0t^aL
Здесь коэффициент умножения М теперь уже зависит от лс0:
Из (11.А. 49) можно сделать заключение, что за счет умножения генерационный источник при х0 дает ток в цепи, который в М(х0) раз превышает первичный генерационный ток. Таким образом, мы можем рассматривать область умножения как фильтр в том смысле, как это использовалось при изложении раздела 11.А.1, поскольку он обладает передаточной функцией вида М(х0). Мы также видим, что коэффициенты умножения, выведенные в разделе 11.7, в ряде частных случаев принимают следующий вид:
1. Инжекция при х = 0:
М р = Л/(о)= —-—-— (11.А.51)
1 - к еЛа£
2. Инжекция при х = L:
М„ = M(l)= (ИА52)
1 - к e*aL
3. Однородная объемная генерация:
L
J/(х0)±Хо
РДог! _ 1
-------------- А.4-Ь~) <11А53)
J qGAdx0
Тот факт, что лавинная область ведет себя как линейный фильтр, важен с точки зрения расчета шума. С учетом (11.А.16) мы знаем спектр шума на выходе фильтра в М(х0)[23] раз отличается от входного спектра шума. Поскольку источники в различных точках лс0 являются независимыми, достаточно рассчитать полный шум в виде вкладов ото всех источников и умножить результат на М(х0)2.
В каждой точке имеются три генерационных источника, обладающие соответствующим шумом:
/ (х ) = дА Є £д.—— (і - е-л“ )
Да
Подставляя эти уравнения в (11.А.56) и используя выражения для М, приведенные в (11.74), мы находим:
І
І; = 2д&уАдС (1 + ап1М)(" М2(х)е Л"Лёх =
{ (11. А. 58а)
= 2<7Ді'АдЫМ (і + а„ЬМ\ + а±м)= 2дАу1М ^ + а"Ш^1 + агШ)
М
Это выражение может быть также переписано в виде:
Г = 2#Ді'1МР(М)
(11.А.58 б)
Р(м) Ь + +
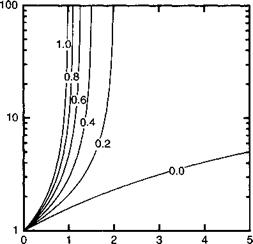
Таким образом, шум состоит из генерационного шума, умноженного на коэффициент лавинного умножения М, играющего ту же роль, что и gв фотопроводнике (смотрите (11.А.43), при этом коэффициент умножения шума Р(М) описывает вклад в шум, обусловленный лавинным процессом. На рисунке 11.А.5 показана зависимость этого коэффициента от произведения аЬ. Заметим, что этот коэффициент минимален, когда к = О или /к = 0, но ассимптотически пропорционален М, когда два коэффициента ионизации имеют одно и то же значение. Таким образом, для получения приемников излучения с высокими функциональными характеристиками, необходимо подбирать материалы и конфигурации смещения, при которых доминирует какой-либо один из этих коэффициентов.
2. Электронная инжекция, т. е. чС(л:0) = /(/,)<?(х0 — Ь). В этом случае мы имеем /= Мп1п(Ь) и в соответствии с уравнениями (11.76)—(11.78):
|
О 5 >. 3 |
|
О Х |
|
|
|
|
|
1р(х)= алМ. п/л^)(^ _ е~д<”)= 1 _ е 40“)
После подстановки в уравнение (11.А.55) и упрощения (заметьте, что еЛо* =
— Мп/( 1 — к + кМп)) это дает:
£
|
С = 2дШп{Ь] |
![]()
|
(11. А. 60) |
![]() М] + а„М„І М2(хУЛса<1х
М] + а„М„І М2(хУЛса<1х
|
КМп + (1-к]2 —- |
![]() = 2^Ау/„(і)[м„2 + кМІ + (1 - 2к)М2„ - (і - к)М„= 2дШМп
= 2^Ау/„(і)[м„2 + кМІ + (1 - 2к)М2„ - (і - к)М„= 2дШМп
Этот результат может быть интерпретирован аналогично предыдущему случаю. Более того, мы ясно видим, что коэффициент умножения шума минимален при к = 0 и резко возрастает по мере приближения ап к а.
3. Дырочная инжекция, т. е. qG(x0) = 1р(0)<?(х0). Этот случай может быть выведен из предыдущего с использованием замены 1пЩ на / (0), ап на ар и, таким образом, к на 1/к, что дает:
ІІ = 2цАу1М рр(м р)
|
Р(М,)= |
|
—мв + к ' |
|
|
|
|
Этот случай представляет практический интерес только тогда, когда ар» ап.
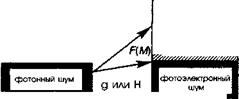
В заключение этого раздела еще раз отметим, что имеется ряд источников шума, поведение которых суммировано на рисунке 11.А.6. Важно подчеркнуть: мы обнаружили, что:
• ![]() Фотонный шум за счет механизма детектирования преобразуется в фотоэлектронный шум, при этом, как мы видели в этом разделе, его «судьба» та же самая, что
Фотонный шум за счет механизма детектирования преобразуется в фотоэлектронный шум, при этом, как мы видели в этом разделе, его «судьба» та же самая, что
|
|
|
Схемный шум 7^ТГ>ГГ/ГГГГГТГГГГ)}ГГЩ |
|
І шум | ^ усиления V/ |
|
Сигнал |
Детектируемый Шум |
Сигнал |
Д или Н |
Детектируемый |
|
|
Шум |
Усиление
Б
Рис. 11.А.6. Различные источники шума фотодетектирования в фотодиоде (а) или в приемнике с внутренним усилением (фотопроводник или лавинный прибор) (6).
И у сигнала, т. е. он «страдает» из-за тех же самых квантовых потерь (rj < 1) и претерпевает то же самое усиление (g в случае фотопроводников и М в случае лавинных фотодиодов), что и детектируемый сигнал.
• шум усиления обладает специфическим характером в том, что касается лавинных приемников излучения с коэффициентом F(M), описываемым (11.А.586);
• шум цепи считывания (т. е. усилитель, интегратор и т. д.) не зависит от усиления фотопроводимости;
Таким образом, понятно, что можно получить выигрыш от внутреннего усиления (усиление фотопроводимости с коэффициентом g или лавинное умножение с коэффициентом М) перед тем, как использовать электронное усиление.
Говоря более точно, если шум усилителя есть <7 u (А Гц1/2) отношение сигнал/ шум для полной электронной цепи дается выражениями (11.73) и (11.А.586):
S / N = __ _________ MAq пФ°______________________ (11.А.62)
Здесь: А есть площадь поверхности, Ф0 — поток фотонов, а rj — квантовая эффективность приемника излучения. Этот результат следует сравнить с отношением сигнал/шум, полученным для случая использования фотодиода в той же самой цепи регистрации, т. е.:
S / N = _ _________________ (11.А.63)
У12Ад2А vjj&o + cr^A v
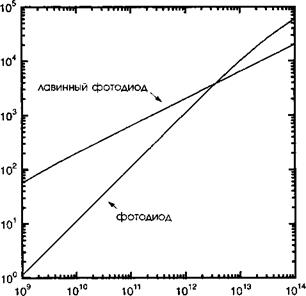
Теперь мы сравним отношение сигнал/шум для фотодиода и кремниевого лавинного диода с к = ос! ап = 0,1 и оспЬ= 3. В этом случае М = 100 и F(M) =12 (смотрите рис. 11.24 и 11.А.5). На рисунке 11.А.7 приведено сравнение (11.А.62) с (11.А.63). Отметим, что использование лавинного фотодиода обладает преимуществами при малых уровнях сигнала, когда мы хотим отделить шум детектирования от шума усилителя. Говоря более точно, это есть случай, когда:
|
|
|
5 *<“ О Х |
|
О S X Ф 3 О Х |
|
-9 -1 Поток излучения (фотон см с ) |
|
Рис. 11.А.7. Сравнение отношения сигнал/шум двух диодных фотоприемников с площадью 1 мм2 при полосе частот 50 Гц. |
![]() X / Jf*_________________________________ ampli 1 ampli
X / Jf*_________________________________ ampli 1 ampli
F(M)-l 2д2Ат) “ F(M)2q2At]
Таким образом, если мы предположим, что световой сигнал образован фотонами с энергией 1 эВ и он детектируется с использованием приемника излучения площадью в 1 мм2 и с квантовой эффективностью 0,5 при шуме усилителя 0,1 пА Гц~1/2, то это приводит к предельному потоку 3,2 х 1012 фотонов см-2 с“1. Таким образом, для мощности падающего излучения менее 0,5 мкВт лавинный фотоприемник излучения был бы исключительным приемником излучения.