Тепловой шум
Для расчета теплового шума мы вначале рассмотрим электрон в полупроводнике, в котором нет ни поля, ни градиента концентрации носителей. Эволюцию функции распределения такого электрона дает уравнение Больцмана (смотрите главу 6):
|
(11-А. 18) |
![]() Э/(у, 0 = /(у, О - Л (у) Э/ г»
Э/(у, 0 = /(у, О - Л (у) Э/ г»
Здесь /(V, /) есть вероятность того, что в момент времени t электрон обладает скоростью V (уравнение (6.7)). Мы использовали аппроксимацию времени релаксации для интеграла столкновений (уравнение (6.12)).^(у)есть распределение Максвелла при термодинамическом равновесии.
|
(11.А. 19) |
![]() Решение этого уравнения получить достаточно просто:
Решение этого уравнения получить достаточно просто:
|
/ Ї |
+ /о (у Л - ехр |
/ ~ Ї ] |
|
Те V / |
1 |
Те /-І |
|
/(*> ')= /(*> 0)ехр |
Если мы фиксируем скорость в момент времени на величине у0, то в этом случае мы имеем /(у0) = <?(у — у0) и (11.А.19) дает причинную функцию распределения, т. е. вероятность того, что скорость в момент времени / составляет V при условии, что в момент времени і = 0 она равна у0:
|
+ /о(у)н-ехр |
|
До |
|
|
|
|
|
|
Комбинированная функция распределения, т. е. вероятность того, что скорость составляет V в момент времени / и у0в момент времени / = 0, соответственно есть:
|
+ /ok)/oW i-exp |
|
CW. |
|
||
|
||
Из этого комбинированного распределения мы получаем автокорреляционную функцию для V при / > 0:
|
+ 0 (11.А.22) |
![]()
|
Rc(v0) |
![]() S„U) = Jdvdv0v^0x/(v, г; v0, 0)= Jdv0v02,/0(v0)exp
S„U) = Jdvdv0v^0x/(v, г; v0, 0)= Jdv0v02,/0(v0)exp
|
В том, что касается стационарных процессов, мы имеем 5^(0 = $^(—1). Более того, если бы г была просто постоянной величиной, то интегрирование (11.А.22) дало бы: |
|
КГ |
|
(11.А.23) |
|
Т |
|
4 kT R |
|
Ц = 4kTGAv = |
|
Av |
|
Спектр мощности шума есть Фурье-образ: £»= Это дает: С (а)- Г Ну 2Т, с(УоК2х/о(Ур) ° 1 + І^(у0) Для обычных электронных частот сотс<< 1 (г имеют величину порядка пс), при этом с использованием (6.16) мы находим для подвижности: |
|
(11.А.24) |
|
(11.А.25) |
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
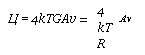 |
|
|
|
Тепловой шум в полосе частот А у
Это последнее выражение может быть интерпретировано следующим образом: тепловая мощность Ri2, рассеиваемая на резисторе R в полосе частот А V эквивалентна средней тепловой энергии 4кТ, рассеиваемой в течение времени Ау~1.
Найдем стандартную дисперсию тока из-за теплового шума при 300 К в резисторе номиналом в 50 Ом при интегрировании сигнала в течение 1 мс. Спектральная ширина составляет 103 Гц, при этом выражение (11.А.29) дает У(4 х 1,3 х 10-23 Дж К"1 х х 300 К х 103 Гц/50 Ом) или 0,57 нА. Этот ток далек от того, чтобы быть пренебрежимо малым.