Геометрический подход к волноводам
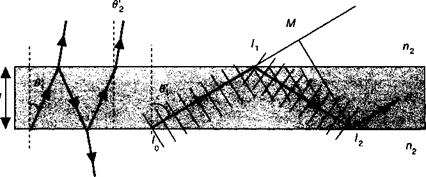
Интерпретацию волноводного распространения света мы начнем с рассмотрения распространения световых пучков. Этот подход позволит нам быстро подойти к интуитивному пониманию концепций, лежащих в основе этого явления. Рассмотрим слой сердцевины, сформированный из диэлектрического материала толщиной с1 и коэффициентом преломления я,, заключенный между двумя очень толстыми (в идеальном случае бесконечными) ограничивающими слоями с коэффициентом преломления пг Световой пучок внутри среды 1 образует угол в' по отношению к нормали к плоскости, разделяющей слои. Затем этот луч за счет преломления переходит в среду 2 под углом в к нормали (смотрите левую часть рисунка 9.1 а).
|
|
|
А |
|
О |
|
Рис. 9.1. Лучевое представление условий, приводящих к оптическому ограничению света волноводом (а). Числовая апертура волновода дается максимальным синусом угла входа для пучка, входящего из воздушной среды (б). |

![]() Б
Б
Вспоминая основные результаты Декарта—Снелля—Френеля, мы можем сделать следующие выводы:
• углы в и в связаны друг с другом соотношением:
(9.1)
• если пх > п2 световая волна в среде 1 полностью отражается, если она падает под критическим углом в'с (полное внутреннее отражение), определяемое соотношением:
![]() (9.2)
(9.2)
![]() (9.3)
(9.3)
Здесь: 01 = л/2 — 9. Заметим, что как общее правило мы сохраняем символ ' для обозначения компоненты, соответствующей углу в; т. е. в' = л/2 — в.
Правая сторона рис. 9.1 а описывает ситуацию, соответствующую полному внутреннему отражению, когда волна становится распространяющейся при условии, что в > 0'с. В то же время мы не должны полагать, что любая электромагнитная волна, удовлетворяющая последнему условию будет волноводной. В действительности же каждое отражение между границами раздела между двумя различными средами будет приводить к дефазировке волны, что будет приводить к ее деструктивной интерференции с самой собой, за исключением случая синфазности волны с волнами, возникшими в результате предшествующих отражений. Это последнее условие хорошо иллюстрируется рисунком 9.1 а. Проследим два последовательных отражения от двух границ раздела в трех точках /0, 1Х и /2. Явно видно, что волна в точке /2 является
Результатом, по крайней мере, двух других волн: волны, которая не испытала отражение и которая соответствует смещению 10М, а также другой волны, испытавшей два отражения, прошедшей расстояние /0/, + /,/2 и получившей вследствие двух отражений фазовый сдвиг (2ф). Эти две компоненты характеризуются разностью расстояний распространения /,/2 - 1{М= /,/2 - ^Дсов2вх = 2ьтгвх1х12 = 2$п2вх х с1/о, о$&с = = 2Жп01 и фазовым сдвигом 2фг, что приводит к дефазировке величиной 2к(кпвх — 2фг, где А: есть волновой вектор, а 2ттх/А^ есть длина волны электромагнитной волны в вакууме. Фазовые сдвиги из-за многократных отражений будут приводить к деструктивной интерференции, если только они не будут кратны 2лг, в результате чего мы приходим к условию самосогласования локализованной волны:
|
2 л/1, |
![]()
|
(9.4) |
Теперь нам остается только подставить это последнее условие в формулу Френеля
(9.3) с тем, чтобы поучить:
|
/2 |
|
1 |
|
Ып2 в, |
|
В. |
|
|
||
|
|||
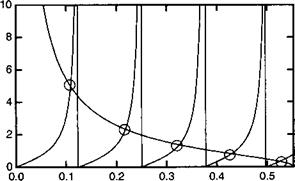
Уравнение (9.5) с неизвестной величиной 8Ш0, позволяет определить различные углы вт,, обеспечивающие волноводное распространение волн в волноводе. При этом мы не забываем, что фазовый сдвиг фг имеет величину в пределах от 0 до п. Рисунок 9.2 иллюстрирует графический метод получения допустимых решений этого уравнения. Когда вт#, изменяется в пределах интервала 0 -> вт#, член в правой стороне периодически проходит через +оо _> о, тогда как член в левой стороне периодически проходит через 0 -> +<» каждые А0/2пхс1. Кроме того рисунок. 9.2 позволяет рассчитать количество Ыт волноводных мод, распространение которых возможно в волноводе. Их будет столько, сколько периодов содержится в интервале 0 -> $ш0с или $пвс/(Л0/2пхс1). Таким образом, мы находим:
(9.6)
|
+ 1 |
![]() N т = т
N т = т
Число разрешенных ТЕ-мод в симметричном волноводе
|
Ф X Ф X Со О А > |
![]()
|
Рис. 9.2. Графическое решение уравнения (9.5) для условий, соответствующих приведенному ниже примеру. |
![]()
|
Ею в |
![]() Здесь 1ги-функция целого числа, а NA есть числовая апертура волновода, определяемая с использованием соотношения (9.2) в виде:
Здесь 1ги-функция целого числа, а NA есть числовая апертура волновода, определяемая с использованием соотношения (9.2) в виде:
^ = (л,2 - п22)1/2 (9.7)
Числовая апертура волновода
Рисунок 9.16 показывает, что числовая апертура представляет собой синус входного угла волновода для лучей, падающих из воздушной среды. В том случае, когда числовая апертура больше 1, входной угол составляет л/2. Уравнения (9.6) и (9.7) показывают, что по аналогии с одномерной ямой, которая всегда обладает связанным состоянием, симметричный волновод всегда имеет, по крайней мере, одну разрешенную ТЕ-моду. Кроме того, уравнение (9.6) позволяет сформулировать условие одномодового волновода:
X < 2ЫА (9'8)
Аналогичный ход рассуждений может быть использован для ТМ-мод (с соответствующей системой уравнений Френеля) и обобщен на случай несимметричных волноводов. В то же время более предпочтительным нам представляется использование более эффективного подхода, основанного на использовании уравнений Максвелла.
Пример----------------------------------------------------------------------------------------------------------------------------------------------------
Рассмотрим волновод на основе слоя 1пСаА5 (я, = 3,9), заключенного между двумя слоями АЮаАз (п2 = 3,0). Числовая апертура волновода составляет NA =(3,92 — 3,02)|/2 = 2,49. В том случае, когда толщина слоя ЫваАБ составляет 1 мкм, волновод будет иметь пять разрешенных мод на длине волны 0,9 мкм.