Оптоэлектроника

Квантовые нити и ящики

Мы уже видели, что полупроводники могут использоваться для создания квантово-раз - мерных структур, которые действуют таким образом, что ограничивают движение носите­лей в направлении z (в направлении роста). Если движение ограничено еще и в другом направлении (например, х) движение электронов в структуре останется свободным толь­ко в одном остающемся направлении у. В таком случае мы можем эффективно сформиро­вать электронный волновод.

В технологическом смысле существуют два общих подхода для реализации та­кого двойного ограничения (смотрите рис. 8.А.1):

1. Для поперечного сегментирования квантовой ямы в в виде нитей может использо­ваться литография.

2. Для этой же цели может использоваться отрицательное напряжение, прило­женное к металлическому затвору очень малых размеров. За счет увеличения электронного потенциала под контактами мы создаем параллельные линейные об­ласти обеднения в квантовой яме за исключением области, лежащей под простран­ством, разделяющим контакты. При увеличении амплитуды приложенного напря­жения поперечный размер электронного волновода может быть уменьшен до пре­делов отсечки, когда от канала в яме ничего не остается.

Очевидно, что уравнение Шредингера для огибающей функции yAj), описыва­ющей электронные состояния в квантовой нити, имеет вид:

(8.А.1)

Рис. 8.А.1. Методы, используемые для формирования квантовых нитей. Фор­мирование ультрамалой меза-структу - ры с использованием литографии (с) и задание поперечной симметричной геометрии обеднения за счет прило­жения потенциала к соответствующим образом текстурированным металли­ческим контактам (б).

Потенциал У(х, г), управляющий процессами в такой квантовой нити, сохраня­ет трансляционную симметрию в ^-направлении. Таким образом волновая функ­ция уАх) допускает выделение плоской волны только в ^-направлении, т. е.:

И*, у, ^'*'*

Функция удовлетворяет двумерному уравнению Шредингера:

-хут^ +У(Х’ *) = Е£і(х, ї)

В общем случае эти уравнения описывают одномерные подзоны с дискретными связанными состояниями |/) в двух измерениях, а также свободное движение в направлении у. Для заданной подзоны / энергия состояния (/, к ) есть:

(8.А.4)

Обобщая ход рассуждений, иллюстрируемый рис. 8.6., можно рассчитать плотность состояний в подзоне, накладывая периодические пределы в направлении у.

(8.А.5)

Напоминаем, что gs есть коэффициент спинового вырождения ^ = 2). Плотность состоя­ний по энергии можно легко найти, записав плотность дп в пределах бесконечно малого интервала энергии й£:

С1п. = Я( £)(!£'= 2й(к)йку (8Л.6а)

В это выражение входит коэффициент 2, поскольку для заданной энергии Е имеются 2 значения /у определяемые (8.А.4). Плотность состояний по энергии в этом случае дается выражением:

А(£)= 4(0 2

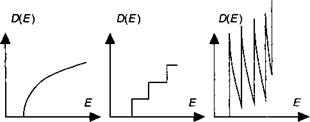
Это выражение характеризуется сингулярностью при Е = Е. (смотрите рис. 8.А.2).

Для решения (8.А. З) в общем случае используются численные методы или апп­роксимации. Тем не менее, если мы представим потенциал в виде прямоугольной нити размерами Ьх х Ь, характеризуемый бесконечными барьерами, решение мо­жет быть легко получено разделением переменных:

£;(*»*)= С„,„: (х, г) = , зт эт (8.А.7)

V х I х 1

Здесь пх = 1, 2, 3, п1 = 1, 2, 3, ... Энергия квантового ограничения, соответству­ющая одномерной подзоне (пх, пу), находится тривиально:

(8.А.8)

Мы видим, что если Ьх» Ьг уровни пх формируют лестницу с маленькими ступенька­ми внутри уровней, что следует из разделения ямы на подзоны по пг. В альтернативном случае, когда Ьх = Ьг два набора уровней не могут разрешиться, при этом многие уровни являются вырожденными.

Теперь мы можем распространить этот ход рассуждений вплоть до нулевой размер­ности. Потенциал, ограничивающий электроны в трех измерениях, способен создать пол­ностью связанные состояниями, обладающие дискретным спектром. В этом слу­чае мы можем говорить о квантовом ящике, квантовой точке или даже об искусст­венном атоме. Квантовые точки можно формировать с удивительной легкостью, осаждая полупроводник с постоянной решетки, сильно отличающейся от этого же параметра подложки другого состава. Необходимая величина рассогласования постоянных решетки приводит к крайне малой критической толщине, как это имеет место в случае 1пА5, осаждаемого на ваАБ. В этом случае 1пАб формирует малень­кие островки на подложке ваАБ, что приводит к квантовым ящикам пирамидаль­ной формы с высотой и шириной нанометрового размера. Рисунок 8.А.2 сумми­рует результаты для плотности состояний для систем с размерностью 3, 2, 1 и 0.