Модуляторы электропоглощения на эффекте Франца—Келдыша
Когда мы прикладываем к полупроводнику статическое электрическое поле, бло - ховские волновые функции уже не представляют стационарные состояния кристалла, т. к. потенциал более не обладает периодичностью межатомного расстояния. Соответствующее изменение в волновых функциях оказывает существенное влияние на оптическое поглощение. В данном случае полупроводник может поглощать фотоны с энергией Ь (о, меньшей ширины запрещенной зоны Е&. Более того, выше запрещенной зоны спектр проявляет осцилляции, накладывающиеся на обычный характер зависимости (%о)— £)1/2, реализующийся в условиях Р = 0. Это и есть т. н. эффект Франца—Келдыша. Как мы увидим позже это явление эффективно используется в электромодуляторах. Начнем с того, что представим формализм, позволяющий описать этот эффект.
Произвольно предположим, что электрическое поле ориентировано в направлении ь В этом случае уравнение Шредингера приобретает вид:
|
(7.А.1) |
![]() 4— + КДг) - е/% ¥(Т) = Еу/(Т)
4— + КДг) - е/% ¥(Т) = Еу/(Т)
Мы можем разложить волновую функцию у/ в базисе блоховских функций |як) = ип к(г)е1кг (решения уравнения в отсутствие электрического поля) в виде:
|
Спроецируем результирующее уравнение на базис функций |7УК), что дает: |
(7.А.2)
(7.А. З)
|
^(Ж|фк)а„(к) = у^|<3ге 'Кги^(гкй„(к)е'кги„к(г) |
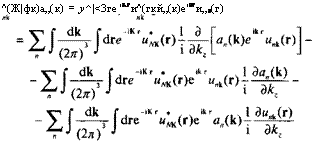 Второй член в последнем уравнении, обусловленный полем, может быть преобразован следующим образом:
Второй член в последнем уравнении, обусловленный полем, может быть преобразован следующим образом:
(7.А.4)
Последний член в этом выражении исключается, т. к. интеграл по к является периодической функцией по к с периодом 2п/а^ где аг есть постоянная элементарной ячейки. С учетом периодичности млк(г) по г и ортогональности базиса другие члены имеют вид:
£ (М£|фк)а„(к) = і + £ іаЛЮАк | СІГИ;К(Г)^Р =
|
(7.А.5) |
![]()
|
При этом: |
Гм,(К) = - рт|дгц*к(г)э“^(г) = у— | (1ги*к(г)ги^к(г)
|
Эд,(Ю Э К, |
![]() В этом случае уравнение Шредингера с коэффициентами а (к) приобретает вид:
В этом случае уравнение Шредингера с коэффициентами а (к) приобретает вид:
ЕР£ г*,(К)й,(К) = [Е -г„(К)>„(К) (7.А.6)
П
Уравнение Шредингера для кристалла в присутствие электрического поля
Последнее уравнение возникает во всех случаях, связанных с наложением электростатического поля на кристаллический потенциал, как это имеет место в эффекте туннелирования через запрещенную зону (эффект Зенера).
С использованием подхода теории возмущений найдем решение, близкое к ^0); сначала мы можем пренебречь влиянием членов, обусловленных зонами спф N(3 этом случае зоны являются несвязанными). Член остающийся в сумме, может быть перенесен на
Право. В то же время не будем пренебрегать им и будем надеяться на то, что я^К) будет играть важную роль только при К = 0 и zNlJ^0) = 0 для экстремума зоны N
При Е=€^0) решение (7.А.6) имеет вид:
|
(7.А.7) |
![]() Я„(К) = ЯдДК,, Кг) = а„(К||( 0)ехрЦ-1[Е - £„(К')]с1К; =
Я„(К) = ЯдДК,, Кг) = а„(К||( 0)ехрЦ-1[Е - £„(К')]с1К; =
|
[і ( |
/ЛЧ /г Я? |
„ ГгкА |
|
— |
Е £„(0) |
Кг+ 1 |
|
ЕЕ [ |
2 ты |
6/Ид, ^ |
|
= ЯдДКп, 0)ехр |
Мы ввели эффективную массу для ТУ1 ной зоны и 1^ = (Кх, К^. В действительности, сделан
Ные аппроксимации являются теми аппроксимациями подхода эффективной массы, которые мы более детально изучим в Главе 8. Теперь мы уже может рассчитать следующую функцию:
(7.А.8)
Она представляет собой ничто иное, как огибающую функцию, описывающую изменение волновой функции стационарного состояния в направлении электрического поля. С этой целью используем следующую формулу (смотрите уравнение (10.4.32) Аб - ромовича и Стегуна):
|
(7.А.9) |
![]() (Зя) ,/3яАі[(Зя) 1/3 х= Jсо8(яг3 + хґ)&
(Зя) ,/3яАі[(Зя) 1/3 х= Jсо8(яг3 + хґ)&
Таким образом мы получаем следующее выражение для огибающей функции:
|
/з |
|
Рі2 К2 Е-е№-%^—еК |
|
|
|
|
Огибающая функция для электрона в зоне N
|
■ . —Г........... г™ .... 1 " 1 |
..... 1 " 'Г ш |
|
____ 1___ 1___ 1___ 1___ |
__ 1___ 1_ |
|
0.6 0.4 0.2 |
|
-0.2 |
|
-0.4 |
|
-10 -8 |
|
-6 |
|
-4 |
|
-0.6 |
![]() В представленном выражении АЦг) есть функция Эйри, которая по определению есть решение уравнения:
В представленном выражении АЦг) есть функция Эйри, которая по определению есть решение уравнения:
|
(7.А.11) |
--<Аі(с) = 0
Сії2
Эта функция стремится к нулю, когда г —> °°. Рисунок 7.А. 1 иллюстрирует общий вид этой функции. В действительности:
|
1 |
|
Ехр |
|
2л/я"г |
|
1/4 |
|
Аі(г) = |
|
|
|
|
При I < 0 функция осциллирует с уменьшающимся периодом:
|
--Г* |
|
1 |
|
-81П |
|
2л[лг |
|
1/4 |
|
Аі (- г) = |
|
|
|
|
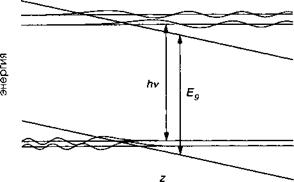 С первого взгляда решение (7.А. 10) может показаться несколько сложным. Однако мы увидим, что поведение функции легко может быть понято. Сначала мы отметим, что аргумент функции Эйри в (7.А.10) равен 0 для ^ = (£— е^О) - Н2К^/2т„)/еР. При £ < %о функция уменьшается экспоненциально. Рис. 7.А.2 показывает, что этот эффект аналогичен туннельному эффекту, когда волновая функция проникает в запрещенную зону полупроводника. При г > функция осциллирует все более и более быстро, что соответствует увеличению кинетической энергии (смотрите рис. 7.1). Более того, решения для других энергий — те же самые за исключением того, что они являются транслированными на Аг0 = АЕ/еР. Одним из следствий этого свойства является то, что нормировочная константа аы(0) не зависит от или Е.
С первого взгляда решение (7.А. 10) может показаться несколько сложным. Однако мы увидим, что поведение функции легко может быть понято. Сначала мы отметим, что аргумент функции Эйри в (7.А.10) равен 0 для ^ = (£— е^О) - Н2К^/2т„)/еР. При £ < %о функция уменьшается экспоненциально. Рис. 7.А.2 показывает, что этот эффект аналогичен туннельному эффекту, когда волновая функция проникает в запрещенную зону полупроводника. При г > функция осциллирует все более и более быстро, что соответствует увеличению кинетической энергии (смотрите рис. 7.1). Более того, решения для других энергий — те же самые за исключением того, что они являются транслированными на Аг0 = АЕ/еР. Одним из следствий этого свойства является то, что нормировочная константа аы(0) не зависит от или Е.
Рис. 7.А.2. В присутствии электрического поля волновые функции С, электронов и дырок перекрываются даже в том случае, если они разделены по энергии на интервал, меньший размера запрещенной зоны Это обеспечивает возможность оптического поглощения фотонов с энергией, меньшей ширины запрещенной зоны.
|
А2*. 2т. |
|
= £в;(А:1)вХ)= №а;(оК(о)ехРр - * 2л [еР |
|
П2к? |
|
К.+ |
|
Е2-£ |
|
6 тг (7.А.16) Где тг — приведенная масса. Из соотношения (7.А.9) мы вновь получаем функцию Эйри: |
|
1/3 |
|
2 тгеР ~ИГ~ |
|
/г=<(оК(о |
|
А1 |
|
Ч1/3 |
|
2 тг |
|
|
|
|
|
|
|
|
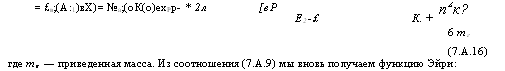 |
|
|
|
|
|
|
|
Существенным моментом является то, что / отличается от 0, когда Е2~ Ех = Н со меньше, чем Е'. Именно этот член ответственен за эффект Франца—Келдыша. Для расчета полной скорости перехода на заданной частоте нам необходимо просуммировать по всем начальным состояниям, т. е. по всем Кц и Ег при этом энергия конечного состояния Е2 составляет Ех + Ьсо. Для этого мы временно опустим константы и вновь подставим их позже при стыковке полученных результатов с формулой при Р = 0. Вводя характеристическую энергию Франца—Келдыша:
|
1/3 |
|
2т |
|
Р = |
|
П2е2Р2 |
|
|
А также безразмерную переменную:
Получаем для суммы по Кц*.
Последний интеграл можно проверить, беря его производную и используя уравнение для определения Аі(г): Аі'Хг) =
При Е -> 0 поглощение в функции Ь а) должно согласовываться с ранее полученным результатом (уравнение (7.24)):
|
(7.А.19) |
При Р 0 и Нсо < Е8, — <*> (7.А.18) стремится к нулю, как этот и должно
Быть. При Е-> 0, к со >Е, £—> ©о мы должны использовать асимптотическую форму (уравнение (7.А. 13), что приводит к:
|
(7.А.20) |
![]() А(П(о, Р = 0)=А^-4'/2 = Р О
А(П(о, Р = 0)=А^-4'/2 = Р О
К 71 у р
Приведенная зависимость имеет такой же характер, как и (7.А. 19). Сравнение (7.А. 19) и (7.А.20) определяет, таким образом, окончательный результат:
|
(7.А.21) |
![]() А(Па>, Р)= аьри2я[Аі,2(-£)+|Аі2(-£)]
А(Па>, Р)= аьри2я[Аі,2(-£)+|Аі2(-£)]
Поглощение в присутствии электрического ПОЛЯ
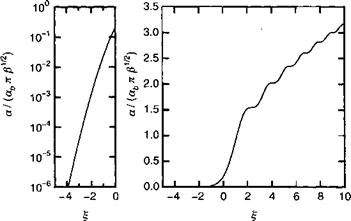
Рисунок 7.А. З иллюстрирует особенности поглощения в полупроводнике в условиях приложенного электрического поля.
Для фотонов с энергией меньше ширины запрещенной зоны наблюдается ненулевой коэффициент поглощения, в то время, как при Нсо > Е наблюдаются осцилляции поглощения в функции энергии фотонов.
|
Рис. 7.А. З. Поглощение в условиях электрического поля в функции энергетического интервала между энергией фотонов и шириной запрещенной зоны £= (Нсо — £)//?, где р— (Й2е2Р2/2тгУ/ъ. Характеристика для области энергий меньше ширины запрещенной зоны (левый рисунок) представлена в логарифмическом масштабе. |
Пример--------------------------------------------------------------------------------------------------------------
Для приложенного электрического поля с напряженностью Е= 10 кВ/см и тг = тетИ(те + /ял)= 0,059/я0 (в случае ваА*) мы получаем характеристическую энергию Франца—Келдыша величиной:
|
Й 2 е 2 Р 2 |
1/3 |
(і,05 х 10 "34 )2 (іО 6 )2 |
1/3 |
|
2 тг V ) |
2 х 0,059 х 9,1 х 10 ‘31 х 1,6 х 10 -19 |
В этом случае поглощение при Ь. со - Е = —8,6 мэВ составляет (смотрите рис. 7.А. З) Д-1) = 0,022 или 2,2% от той величины, которая была бы при Нсо — Е& = +8,6 мэВ в отсутствии приложенного поля.
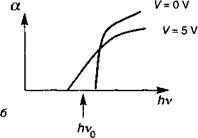
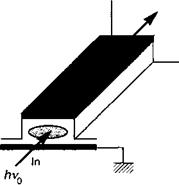
Этот эффект используется в модуляторах на эффекте Франца — Келдыша. Основной принцип их функционирования достаточно прост (смотрите рис. 7.А.4). На полупроводниковый волновод (с шириной запрещенной зоны Eg) наносится металлический электрод для формирования барьера Шотгки с полупроводником (см. главу 10).
При приложении разности потенциалов V между этим верхним электродом и омическим контактом с тыльной стороны полупроводника мы вводим электрическое поле напряженностью F= V/d, где d — расстояние между верхним и нижним контактами (для минимизации какого-либо падения напряжения из-за эффектов пространственного заряда уровень легирования полупроводника выбирается достаточно низким). Приложение разности потенциалов величиной 5 В к межконтактному зазору величиной 1 мкм приводит к напряженности электрического поля 50 кВ/см, что соответствует характеристической энергии р = 25 мэВ. В результате этого фотоны, распространяющиеся в волноводе с энергией Eg — 25 мэВ будут испытывать поглощение, в 100 раз большее по сравнению со случаем отсутствия поля. Из этого легко видно, каким образом мы могли бы использовать такой прибор для преобразования электрического (изменяющегося во времени) сигнала в оптический сигнал.
Такие приборы называются модуляторами электропоглощения на эффекте Франца-Келдыша. Модуляторы этого типа являются чрезвычайно быстродействующими (с максимальной рабочей частотой, лежащей в диапазоне десятков ГГц), так как для своего функционирования они не требуют пространственного смещения электрических зарядов. Что не имеет места, например, в случае SEED-модуляторов (приборов на основе собственного электрооптического эффекта, смотрите дополнение 8.В).
|
5 Li |
|
Out |
![]()
|
.выход |
![]()
|
Свет |
Рис. 7.А.4. Функционирование электрооптического модулятора на эффекте Франца - Келдыша.