Оптическая восприимчивость полупроводника
Теперь мы можем рассчитать оптическую восприимчивость, связанную с переходами из валентной зоны в зону проводимости. Рассмотрим полупроводниковый кристалл объемом У в условиях квазиквантования. Предполагается, что структура валентной зоны и зоны проводимости является параболической и описывается соответствующими эффективными массами ту и /яс. При условии, что оптические переходы являются вертикальными, попробуем найти оптическую восприимчивость связанную с переходами при постоянной величине к между валентной зоной и зоной проводимости. Уравнения (7.4) и (7.(9) дают связь между валентной зоной £(к) и зоной проводимости Ес(к) в условиях связи через оптический переход (смотрите рис. 7.1):
|
V |
|
Тс ту |
|
Ь2 к2 Ес(к)-Ех,(к) = ^- |
|
|
|
|
![]()
Где к есть модуль вектора к. Для упрощения (7.12) полезно ввести приведенную эффективную массу:
|
(7.13) |
![]() 1 1 1
1 1 1
Тг тс тх,
Приведенная эффективная масса
Безразмерная оптическая восприимчивость, связанная с переходом между ква - зидискретными уровнями £(к) и £(к), в этом случае дается (3.26):
|
|
Где хДк) (= хус в соответствии с нашим предположением о независимости диполь - ных матричных элементов от к) есть элемент перехода в направлении Ох, выбранном произвольно для упрощения обозначений, ^с(к) = (£(к) - £(к))/й и Т2 есть время релаксации электронов в зонах. Л^(к) и ТУ (к) представляют концентрации носителей (см-3) на уровнях Ес и £. В этом случае полная восприимчивость определяется суммированием членов восприимчивости (7.14я) по волновым векторам к зонной структуры, т. е.:
|
|
|
К(Ю-ЛГС(Ю] (7.146) |
Где множитель 2 связан с тем фактом, что для каждого вектора к имеются 2 спиновых состояния. Предположим, что объем виртуального ящика достаточно большой, чтобы суммирование заменить интегрированием по к:
|
|
(7.15)
Правило эквивалентности между суммированием по к и интегрированием по к и энергии Е
Где плотность р(к) выражена в 1/(см_3), р(Е) — в 1/Дж, а множитель 2 обусловлен спиновым вырождением. В изотропной среде микроскопические плотности #с(к) и #(к) в (7.14) определяются /?с(к)с13к и /?Дк)с13к, где рс(к) и рДк) равны и даются (5.17), при этом рс(к) = ру(к) = 2 К/8пъ = У/Ая7, (мы умножили результат на 2 для того, чтобы учесть вырождение по спину, при этом напоминаем, что У есть объем кристалла). К этим членам мы должны добавить выражение, соответствующее термическому квазиравновесию: а именно мы должны ввести функции Ферми—Дирака/с(Ес(к)) и fv (Еу (к)), описывающие вероятности заселенности для уровней £(к) и £(к) и приведенные в (5.38) раздела 5.6:
1 + Е, <7.16»)
/* = _____ 1_____
] + Р(Е-Е'.)'*Т
ЕРс и ЕРу есть квазиуровни Ферми для электронов и дырок (заметьте, что в данном случае/у отличается от (5.44), поскольку здесь мы используем вероятность того, что состояние валентной зоны занято электроном). В этом случае бесконечно малую разность плотности ТУ — ТУ в (7.14) для элемента с!3к можно заменить на:
N - N ~ ^к[/Д£(к)]{1-/Д£(к)]} ~/с [£(к)]{1 -/Д£(к)]}] =
(7.16 б)
Таким образом, оптическая восприимчивость получается интегрированием (7.14) по первой зоне Бриллюэна или:
*(«) = [ла3к{дК(к)]- /еК(к)]} - й>ге(к)]г - / (7Л7)
£0Й [®-^(к)]2Г22 +1
Мы предполагаем, что теории Кейна (смотрите дополнение 5.В) матричный элемент не зависит от к. Требование сохранения энергии может быть записано с использованием (7.4), (7.12) и (7.13) в виде:
Ьсо„=Ес{Ъ)-Еу(Ъ) = ^ + Ее 1тг
Ес(к) = Ее+^£- (7.18)
П2к2
Ад = -
2т„
Поскольку волновые векторы к и энергии фотонов Н су^ связаны, мы можем проинтегрировать (7.17) по частотному интервалу падающих фотонов с использованием выражений (5.19) и (5.20):
Р'М = = - Ц^У /ь)'ПМ' (7.19л)
2я >
Или вновь:
|
Л(^)=-Л 2 л |
![]() Щс- (Е - )|/2 (7.19й)
Щс- (Е - )|/2 (7.19й)
А ,
Комбинированная плотность состояний (Дж-1 см-3)
Выражение (7.19) описывает комбинированную плотность состояний, связанную через энергию фотона Нсо. Подставляя последнее выражение в интеграл (7.17), мы получаем основное соотношение настоящего раздела:
^=13^ ?рХа^свЖЕ*)- 1 (7.20)
(со-а)КУТ2 +1
Оптическая восприимчивость, связанная с межзонным переходом в полупроводнике
В этом выражении связанные энергии £ и Ес являются функциями Н со посредством соотношений в (7.18). Коэффициент поглощения связан с мнимой частью оптической восприимчивости через (3.36), т. е.:
А(а>)=— Хы (7-21)
Ся„Р
ИЛИ
,2 v2
«И= Щ *'*(° х Г Р](юк)юк/, (£„)- /С{ЕС%--------------------------------- —уТ Ттг (7'22)
Е0Ьпорс ^ {а-о)кУ+ /Т2
Последнюю формулу легко упростить, если заметить, что лоренциан ведет себя как функция Дирака в сравнении с более медленно меняющимися функциями под знаком интеграла. В результате мы получаем коэффициент поглощения (в см-1) в виде:
А(а>)= ру(а>)|/,(Ла>) - /,(»®)] (7.23)
£0ЙИорС
Или вновь:
А{со)= - у(са)= а0(й) )(/„(/гй))- /Дйю)] (7.24)
Поглощение и усиление в полупроводнике (см-1)
Где у(со) есть усиление полупроводниковой среды, а а0(со) есть поглощение опустошенной зоны проводимости, при этом:
3/2
АМ-^кхг) ,7'2So)
Поглощение опустошенной зоны проводимости (см-1)
Функции/Хй со) и fv(hco) являются функциями Ферми—Дирака:
1 + ехр §Е с (hco)- Е F / кТ }
(7.256)
E'(f><»)= Eg+^(h<o-Eg)
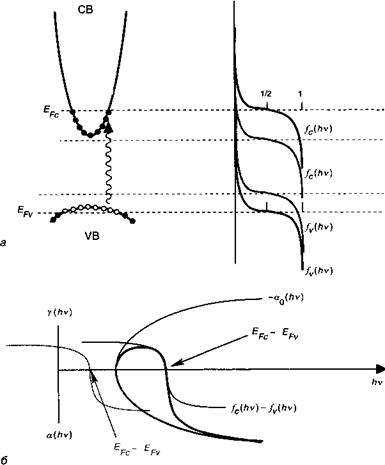
Уравнение (7.24) показывает, что поглощение в прямозонных полупроводниках для фотонов с энергией, большей ширины запрещенной зоны, возрастает как ^1(Нсо — £) (смотрите рис. 7.2). Уравнения (7.23)—(7.24) позволяют описать оптические характеристики полупроводника в условиях отклонения от термодинамического равновесия.
Условие оптического усиления (т. е. а(со) < 0) дается соотношением:
/с(Псо)-/у(Псо)> 0 (7.26а)
Или иначе с учетом (7.256) и (7.25<?):
ЕРс - ЕР>Ь с* (7.26 б)
Условие Бертрана—Дюррафура
|
Рис. 7.2. Представленные рисунки показывают эволюцию кривых поглощения и усиления в функции положения квазиуровня Ферми. Тонированные (жирные) линии соответствуют слабому (сильному) отклонению от равновесия. В этом случае среда поглощает все фотоны с энергией, превышающей ширину запрещенной зоны. Как только энергетический интервал между квазиуровнями Ферми превышает ширину запрещенной зоны, все фотоны, обладающие энергией в диапазоне между Е& и ЕР - ЕРу, начинают усиливаться (условие Бернара—Дюррафура) . |
Это последнее уравнение утверждает, что усиливаться будут лишь те фотоны, которые обладают энергией, меньшей энергетического зазора между квазиуровнями Ферми. Эти квазиуровни связаны с неравновесной заселенностью N условием, полученным в разделе 5.6:
N = рс{Е)------------- г-!--------------- ЛЕ (7.27)
Ъ 1 +ехр[(£- ЕР)/кТ
Это выражение относится к квазиуровню Ферми для электронов ЕРс, и аналогичная формула имеет место для квазиуровня дырок. В условиях положительного усиления кривая, описываемая (7.23), называется кривой усиления в полупроводнике. Рисунок 7.2 иллюстрирует эволюцию кривой усиления в функции возрастающего отклонения от термодинамического равновесия.