Оптоэлектроника

Фрелиховское взаимодействие

Фононы представляют собой нестационарное возмущение периодического потенциала кристалла, определяющего электронные состояния в зонах. Такое возмущение естествен­но приводит к возможности рассеяния электронов из одного состояния в другое в соот­ветствии с золотым правилом Ферми. В неполярном полупроводнике (таком, как 81) по­тенциал взаимодействия, связывающий электроны с фононами, в своей основе имеет тот факт, что искажения решетки изменяют зонную структуру пропорционально амплитуде относительного смещения атомов. Например, локальное сжатие из-за акустической вол­ны приводит к локальному увеличению ширины запрещенной зоны и возрастанию энер­гии состояний в зоне проводимости (смотрите рис. 6.Б.4). В адиабатическом приближе­нии электрон в этом случае подвергается воздействию потенциала, пропорционального амплитуде деформации а этот потенциал может затем индуцировать переходы, т. е. элекг - ро-фононные столкновения.

Естественно, что такие процессы (называемые рассеянием на деформационном потенциале) имеют место также и в полярных полупроводниках (например, в СаАБ),

6. Б. Оптические фононы и фрелиховское взаимодействие 239 Зона проводимости

Валентная зона

Х

Рис. 6.Б.4. Индуцированное фононами изменение запрещенной зоны (называемое де­формационным потенциалом) действует на электроны как потенциал рассеи­вающего центра.

Но в этом случае проявляются дополнительные взаимодействия из-за того факта, что фононы создают поляризационные и электростатические поля, следующие за фононом. В случае акустических фононов мы говорим о пьезоэлектрическом эффек­те. В случае оптических фононов электростатическое поле приводит к электрон - фононному взаимодействию, называемому взаимодействием Фрелиха. Фрелиховс­кое взаимодействие оказывает более сильное влияние по сравнению с деформаци­онным потенциалом, поэтому оно и обсуждается в этом разделе как иллюстрация электрон-фононного взаимодействия.

Поскольку кристалл является полярным, в этом случае осуществляется перенос заря­да е от атомов х к атомам у. Таким образом, деформация, вызванная фононом, приводит к поляризации:

Р = г*(х-У)у (6.Б.23)

При этом величина заряда составляет р = — V • Р. Для оптического фонона с волновым вектором q мы имеем:

Р(г, 0 = - е* у гц • (X - У) ехрОч • г - ш,0 (6.Б.24)

Из этого выражения мы видим, что ЬО-фононы могут индуцировать заряд. В этом после­днем случае уравнение Пуассона дает нам электростатический потенциал:

Кпа(г> 0 = ~ У)ехР('Ч г - (6.Б.25)

Это и есть тот потенциал, с которым электрон может взаимодействовать. Матричный эле­мент, который описывает взаимодействие между начальным электронным состоянием к и конечным состоянием к' есть:

(к|-*К,(г)|к'> = ‘ [М*(Г)Мь(Г)е"- + к-к’'с1г =

£ £п V а V ) ,

(6.Б.26)

— ее* N X — У 1 Г, ч.

—4'*-‘ТГ1 1

При этом квадрат его модуля дается выражением:

|(к|- ^Ик')|2 = Ю (6-Б-27>

Здесь А есть символ Кронеккера, а интеграл перекрытия тот же самый, что был введен ранее при обсуждении примесного рассеяния (уравнение (6.33)). Перед тем,

Как мы сможем использовать золотое правило Ферми, нам необходимо определить еиХ - У

Для определения е* мы используем следующий аргумент: в нашей модели Т0- фононы обладают частотой ахто = >/(2к/тк6), амплитуда колебаний (как реакция на воздействие осциллирующего поля с частотой со) вблизи саТО дается соотношением:

-<у2 (X - У) = —тп6со2то(Х — У) + е Е (6.Б.28)

Это, в свою очередь, определяет поляризацию:

Р = Е-------------------------------------------------------- (6.Б.29)

(®г0 - а2)

При этом проницаемость дается выражением:

Е(со)= е0е„ + -——------------------------------------------------------ ^ (6.Б.30)

"•^У (®ТО - (О1)

В частности, «статическая» проницаемость при со« сото составляет:

£0£я = £0С_ + ^ ^ 2 (6.Б.31)

Т„,Усо20

В случае ЬО-фононов поле возрастает в результате поля наведенной поляризации —е (X— У)(М/У)/е^ что приводит к дополнительной восстанавливающей силы:

- со2 (X - Г )= - т^о{X - ¥)+ {Х-¥)+е*Е (6.Б.32)

При этом реакция системы определяется соотношением:

Р_ = е*2 N / т„ЛУ = е*2 N /т^У (6.Б. ЗЗ)

Е + (е*2 N / е0е_т„. У)-а2] (р10 - т2)

Частота соио превышает <уто. Таким образом, мы можем определить эффективный заряд е:

В ^ = «то £ о (*« ~ е - ) = (е0е, - ®то ) (6.Б.34)

К4

В то же самое время мы получаем соотношение Лиддейна—Закса— Теллера:

(6.Б.35)

Так, что:

Л*2 Г ( ~

(6.Б.36)

И наконец, амплитуда моды может быть определена из принципа соответствия, делая классическую энергию моды эквивалентной числу фононов в моде (Уравнения (6.Б.20) и (6.Б.21)):

|* - У|2Л^ = я,»®«. (6.Б.37)

В этом случае результат для скорости перехода, близкий к окончательному, прини­мает вид:

2я}< ■ ■ V'2

А

* е2Йй.о „(і 1

Д,.1* Ч

Этот результат относится к столкновению, при котором ЬО-фонон поглощает­ся, а его энергия передается электрону. Ранее мы говорили об использовании уравнения (6.Б.37). В действительности, при корректной квантово-механичес­кой трактовке этой проблемы мы должны были бы выразить оператор Х—¥ че­рез операторы рождения и уничтожения, соответствующие гамильтониану в (6.Б.20). После чего процедура становится полностью аналогичной электрон - фотонному взаимодействию, рассмотренному в разделе 3.5.1. Таким образом неудивительно обнаружить, что выражение (6. Б.38) остается действительным для поглощения фононов. В случае эмиссии фононов мы должны заменить пч на пя + 1, что соответствует сумме стимулированного и спонтанного излучения фонона:

/(к, к')<Я£(к) + К1 (6.Б.39)

'Л

Интересно отметить, что включение стимулированного излучения обеспечивает деталь­ный баланс при термодинамическом равновесии:

■и* -> к')/еч(к)[ 1 - /чт = 5аЫ(к к')/еч(к')[ 1 - /„(к)] (6.Б.40)

При этом удается распределением Бозе—Эйнштейна (6.Б.22), а^ч определяет­ся распределением Ферми—Дирака (5.38). В этом случае разностный поток частиц между этими двумя состояниями равен нулю.

Исходя из уравнений (6.Б.38) и (6.Б.39), мы можем рассчитать полную скорость рассеяния из-за фрелиховского взаимодействия с участием оптических фононов.

*(*)=£-» к'> + £^т(к к')

Используя аппроксимацию, что /(к, к') = 1, мы находим:

2 л

К + к' - 2кк'ц

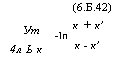При этом к'2 = к2 ± 2 тН(оор/Ь2, что, в конце концов, дает:

-Л? + ^Е - Иа)01

Е Лсо^т

■{Ё - ^Е - Лсо01

АяєпєЛ2 л/2тЕ

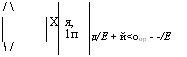(6.Б.43)

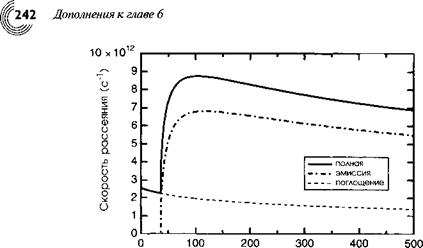
Рисунок (6.Б.5) демонстрирует зависимость Л от £для ваЛз. Естественно, что эмиссия фононов имеет место только выше определенного энергетического порога Е> Нсо из-за того факта, что после излучения фонона электрон обязательно дол­жен обладать только положительной остаточной энергией. Таким образом, мы ви­дим, что электрон-фононное взаимодействие является чрезвычайно эффективным в рассеянии избыточной энергии электрона (на временной шкале процесс проис­ходит в течение временного интервала порядка 100 фс). Таким образом, это взаи­модействие играет фундаментальную роль в механизмах оптической релаксации.

Важно также отметить, что для рассеяния (неупругого и анизотропного), про­исходящего через фрелиховское взаимодействие, в общем случае мы не можем оп­ределить время релаксации. Таким образом, расчет подвижности требует более слож­ного решения (по сравнению с (6.22)) уравнения Больцмана.