Предел Шавлова—Таунса и сила ланжевеновского шума
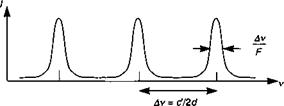
Одной из наиболее упоминаемой особенностей лазерного излучения (помимо его яркости) является его высоко монохроматический характер. Может возникнуть вопрос: «Что же ограничивает спектральную ширину лазерного излучения?» В качестве причин мы могли бы подумать с достаточной долей основательности о зеркальности резонатора или ширине атомных переходов, участвующих в стимулированном излучении. Однако оба эти предположения в действительности неправильны! В действительности, учет этих факторов приводит к выражениям на несколько порядков величины большим того, что наблюдается! Например, для резонатора Фабри—Перо (с длиной d и коэффициентом отражения зеркал г, смотрите рис. 4.Г.1) зеркальность резонатора F и ширина резонанса Фабри—Перо Avc даются выражениями (прочитайте дополнение 9. Г):
|
Рис. 4.Г.1. Ширина полосы пиков пропускания в резонаторе Фабри—Перо равна меж- модовому интервалу &у= с /2с1, деленному на зеркальность резонатора. |
2К
|
1 - г |
![]()
|
(4.Г.1) |
А = 1 С = 1
V° F 2d 2ктс
Где г — время жизни фотонов в резонаторе, определяемое (4.24б). Для резонатора длиной 10 см и коэффициентом пропускания 10-2 мы получаем зеркальность 628 и ширину полосы 2,4 х 106 Гц, что ярко контрастирует с экспериментальными значениями ширины полосы лазерного излучения порядка 1 Гц для определенных лазеров. Возможные вклады из-за ширины атомных переходов, а также их частот, имеют порядок ГГц (смотрите таблицу 4.1). Для понимания чрезвычайно малых значений ширины полосы, связанной с лазерным излучением, нам необходимо возвратиться назад и до определенной степени модифицировать динамические уравнения, приведенные для фотонов в резонаторе (4.А.12). Для начала напомним, что электрическое поле Е(х, /) в любой точке лазера дается выражением Дх, /) = Яе(Дх, /)еНй"), где временная зависимость огибающей функции Е(х, /) описывает временную эволюцию электромагнитного поля вследствие лазерного усиления. Эта зависимость намного слабее, чем колебания электромагнитного поля, даваемые е_1й". Заменим в (4.А.12) число фотонов в резонаторе Р на огибающую функцию электрического поля £(/), определенную в любой точке резонатора, предполагая, что входное зеркало находится в точке х = 0, и напомним, что связь между двумя величинами дается соотношением (см. (2.77):
|
Р = |
![]() (4.Г.2)
(4.Г.2)
2hco
Где є —диэлектрическая постоянная среды (є= £0п2ор)- Отметим, что член спонтанной эмиссии (член + 1 в (4.А.12)) ничего не говорит нам о моменте спонтанного освобождения фотона. Таким образом, заменим его силой F(/), которая будет использоваться для описания хаотического характера этого излучения. В этом случае мы получаем:
D Е 1 dt + 2
(4.Г. З)
Уравнение Ланжевена
Где f{t) — сила Ланжевена, которая обладает следующими характеристиками:
• F{t) является стохастическим процессом случайной переменной с нестационарным характером. Рис. 4.Г.2 описывает такой стохастический процесс. Функция Дг, в) случайно выбирается в момент t = — а 9 — событие, принадлежащее
Рис. 4.Г.2. Стохастический процесс является стохастической функцией /(/, в), каждая реализация 0 которой приводит к функции /(/). При заданном времени tf(t, в) есть произвольная переменная.
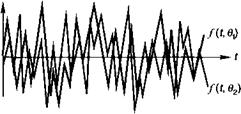 Ансамблю возможных результатов Q. Для каждого толчка (т. е. для каждой величины в) F(t, в) является функцией времени t и для каждого значения времени t F(t, 9) является случайной переменной.
Ансамблю возможных результатов Q. Для каждого толчка (т. е. для каждой величины в) F(t, в) является функцией времени t и для каждого значения времени t F(t, 9) является случайной переменной.
F{t) является эргодическим процессом (смотрите дополнение З. А), что означает идентичность временных и статистических средних в любой момент времени t
|
F = pM)d0 = liml JVM)!/ |
![]() Т /2
Т /2
(4.Г.4)
£2 “ - f/2 Процесс не обладает памятью, т. е. случайные переменные F(t) и /*(/ + t) не скоррелированы для любого тф 0:
F(t)F*(t + r)= AS(t) (4.Г.5 a)
Где A — константа, которую еще надо определить. Далее предположим, что:
F(t)F(t + T)= 0. (4.Г.5 б)
Это не является абсолютно необходимым (это может быть записано в виде BS(t)), но это сильно упрощает расчеты.
Наконец, F(t) — процесс с нулевым средним:
|
(4.Г.6) |
![]() F(t) = 0.
F(t) = 0.
Запишем теперь решение (4.Г. З). Можно легко показать, что решение дается выражением:
T
|
(4.Г.7) |
![]() E(t)= J
E(t)= J
Где мы временно положили, что:
|
V - |
![]() (4.Г.8)
(4.Г.8)
Решение (4. Г.7) может быть интерпретировано как отклик системы с линейным усилением (когда отклик на импульс изменяется как е"') на случайное возбуждение вида /(/). Это является классической проблемой электроники (смотрите рис. 4.Г. З). Сначала мы рассчитаем среднюю величину электрического поля Д/) из (4.Г.6):
(4.Г.9)
Дисперсия поля E(t) дается выражением:
|£(/]2 = Jр*(ГУ('~г)At’ = Jdt'jdҐР(ґ)Р*(ґУ^-''-ґ) (4.Г.10)
E(t)
|
S(a>) |
![]() |SMl20e(w>
|SMl20e(w>
Рис. 4.Г. З. Система с линейным усилением $(со) преобразует стохастический процесс со спектром gc(co) в стохастиченский процесс с gs(c0) = 5(со)\(со).
С учетом того факта, что система не обладает памятью (4.Г.5) это последнее выражение принимает вид:
|Ј(r)|2 = = Ajdt'e2*'-') (4.Г.11)
Или, заменяя v на ее величину в виде (4.Г.8):
|
... |
![]() А
А
1 light
Или вновь, вводя число фотонов и с помощью (4.Г.2):
|
(4.Г.126) |
![]() EVA 1 _[g(G/4*,-t/O _ iJ
EVA 1 _[g(G/4*,-t/O _ iJ
P =
2hco (G /rligh, — 1/rJ
Сравнивая этот результат с аналогичным результатом, полученным в рамках Дополнения 4.А (смотрите (4.А. 13)), мы видим, что два подхода приводят к идентичному результату при идентификации А в виде:
SHAPE \* MERGEFORMAT ![]()
|
А = |
![]()
|
(4.Г.13) |
![]() 2Gb со light ^
2Gb со light ^
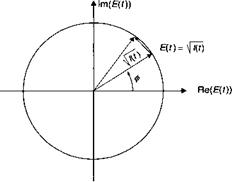
Подход, основанный на уравнении Ланжевена лучше, чем подход «избыточного фотона», введенный в дополнении 4.А., в том смысле, что он описывает хаотичную динамику, связанную с лазерным излучением. Теперь мы введем амплитуду /(Г) и фазу ф{{) электрического поля (смотрите рис. 4.Г.4):
|
(4.Г.14) |
![]() E(t) = V7(0e"
E(t) = V7(0e"
Очевидно, что /(/) и Д/) представляют стохатические процессы. Подставляя (4.Г.14) в (4.Г. З), получаем следующую систему дифференциальных уравнений:
|
(4.Г.15а) (4.Г.156) |
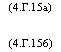 ^- + 2vl = 41 Re[/XOe"] d /
^- + 2vl = 41 Re[/XOe"] d /
 D Ф _ 1 dt ~ iV7
D Ф _ 1 dt ~ iV7
Рис. 4.Г.4. Френелевское представление амплитуды и фазы электрического поля. Под влиянием силы Ланжевена вектор £(/) вращается в плоскости (говорят, что фаза имеет диффузный характер), в то время как амплитудуа остается, в основном, неизменной.
Мы видим, что в (4.Г.15я) / демпфируется членом 2VI. Как следствие, амплитудные флуктуации лазеров очень малы и ими часто пренебрегают. Мы проведем этот расчет в дополнении 13.Г применительно к полупроводниковым лазерам. Однако, уравнение (4. Г. 156) не содержит такого демпфирующего члена по фазе. Таким образом, фазовые флуктуации будут значительны. Этот эффект возникает из - за хаотичных временных характеристик, связанных со спонтанным излучением. Мы перепишем (4.Г.156) в следующем виде:
^[/■(/)е-Г*(/)е **] (4.Г. 16)
Где с учетом слабых флуктуаций по амплитуде / мы заменили / на ее среднюю величину. Уравнение (4.Г.16) формально может быть проинтегрировано следующим образом:
Г
-*(0= (4.Г.17)
Ясно, что средняя величина ф равна нулю. В то же время ее дисперсия дается выражением:
(4.Г.18д)
Это последнее выражение может быть существенно упрощено, если мы используем (4.Г.5) и, кроме того, предположим, что:
/•('У* = Е((У'* (4. Г. 186)
Это последнее выражение обычно выполняется несмотря на то, что процессы Риф являются явно коррелированными. В этом случае уравнение (4. Г. 18) принимает вид:
__ / / _______________ _________________________
Дф1 =~ Г ё/' Гс1/'[/г(/')^’*(г')+ =
4 / J J
'* (4.Г.19)
/0 г0 г0
В этом выражении мы видим, что стандартная дисперсия фазы изменяется со временем в соответствии с соотношением:
Д0 = 7л7 = ^('-О (4.Г.20)
Мы видим, что уравнение (4.Г.20) принимает вид диффузионного уравнения, где константа диффузии О дается О = А /21 или выражением для А в (4. Г. 13) и для / в (4.Г.2) и (4.Г.24в):
Р = ± = ^,1.11 (4.Г.21)
21 2 еттУ гПсоР 2 г|18„, Р К }
Выше лазерного порога усиление (7 фиксируется на своем пороговом значении, определяемом = 1/т. Более того, (4.Г.1) устанавливает, что ширина полосы
Холодного резонатора (т. е. ширина полосы резонанса Фабри—Перо) дается соотношением: Ду = 1/2ят. В окончательном виде коэффициент диффузии для фазы записывается в виде:
£> = (4.Г.22)
Коэффициент диффузии по фазе
Теперь нам остается только рассчитать ширину полосы излучения лазера. Для этого запишем электрическое поле, соответствующее лазерному излучению, в каноническом виде, описанном в начале этого раздела:
£(,)= И^йе-“'] - * £'(/)е"''] (4.Г.23)
Где со0 — частота излучения лазера. Из дополнения З. А мы знаем, что спектральное распределение сигнала дается Фурье-образом автокорреляционной функции (уравнение (З. А. 13)). Это есть теорема Винера—Хинчина (смотрите рис. 4.Г. З). Эта автокорреляционная функция может быть рассчитана с использованием записи:
|
(4.Г.24 а) |
![]() Е(г)Е(г + т)= + г)е 1<ч>(г+г) + £*(/ + г)е'^(г+г^ ^(/)е 1<ч/ + Е*^)ъщ'
Е(г)Е(г + т)= + г)е 1<ч>(г+г) + £*(/ + г)е'^(г+г^ ^(/)е 1<ч/ + Е*^)ъщ'
Или вновь:
£(/ + г)£(/)=^[£(/ + т)£*(/)е 1<ч> + к. с.] (4.Г.24 б)
Заменим электрическое поле £(/) на его выражение в (4.Г.14) и вспомним, что амплитуда флуктуаций / достаточно мала, чтобы гарантировать нам ее замену на среднее значение:
Е(г)Е(г + т)= + т)1^У'(ф('*г)-т (4.Г.25)
Мы уже встречали среднюю величину ек*'+г) _ в (З. А. 16) в предположении, что процесс имеет пуассоновский вид. Делая то же самое допущение в отношении 0(О> находим:
Е!<,(»«)-,(О) = е~т*! = е4/>г (4.Г.26)
Где 8ф2 есть дисперсия фазовых флуктуаций. И, как следствие, выражение для автокорреляционной функции (4.Г.24) принимает вид:
Ох{т)= Е({)Е({ + т) = — /е + к. с. = -~е 2°г соб(со0т) (4.Г.27)
|
2 |
![]() 4
4
Спектральное распределение для Е(со) в этом случае дается теоремой Винера— Хинчина (З. А. 13), т. е. с использованием Фурье-образа (4.Г.27) или:
{со)=ЁЩ = !~ ------- Ц2*г/А <4Г28>
Л (о)-о)0) + О1 /4
Используя выражение для коэффициента диффузии в (4. Г.22), мы находим, что ширина полосы спектрального распределения лазерного излучения (которая может быть измерена, например, с использованием дисперсионного спектрометра) дается выражением:
Ду5Т = Цл - (4.Г.29)
Ширина линии Шавлова—Таунса
Таким образом, мы заключаем, что ширина линии лазерного излучения есть ширина полосы резонатора Д ус, деленная на число фотонов в резонаторе (довольно значительное число). Таким образом, теоретически ширина полосы лазерного из-
|
|
Лучения может быть крайне малой. Уравнение (4.29) может быть представлено в более доступном для расчетов виде за счет использования (4.Г.1) для Дк, а также соотношения (4.30), связывающего число фотонов в резонаторе Р с мощностью лазерного излучения
Р, Я=Р— (4.Г.30)
В этом случае уравнение Шавлова—Таунса принимает вид:
|
Д VsT = ~2лгТр1 <4-Г'31> |
![]() H V
H V
>
Ext
Уравнение Шавлова—Таунса
Пример----------------------------------------------------------------------------------------------------------------------------------------------------
А) Ширина линии излучения лазерного резонатора на основе №3+:УАС (Иу = 1,17 эВ, пор = 1,82) длиной 1 см, с прозрачностью зеркала 0,5% (или фотонным временем жизни 24 не) и мощностью излучения 1мВт составляет Дк8Т = 1,17 х х 1,6 х 10-19 Дж/(2я-х (24 хЮ-9 з)2 х 10_3 Вт) или 5 х 10“2 Гц.
Б) Ширина линии излучения полупроводникового лазера (Иу = 1,4 эВ, пор = 3) длиной 100 мкм, имеющего зеркала с прозрачностью 30% (что соответствует фотонному времени жизни 6 пс), а также мощность излучения 1 мВт составляет Дк8Т = 1,4 х 1,6 х 10“19 Дж/(2;гх (6 х 10-12 8) х 10_3 Вт) или 1 М Гц.