ФИЗИКА ПЛАЗМЫ

АЛЬФВЕНОВСКАЯ НЕУСТОЙЧИВОСТЬ В ПЛАЗМЕ С ПЛЕЩУЩИМИСЯ ИОНАМИ

Отмечается, что в плазме с плещущимися ионами альфвеновская неу­стойчивость принимает характер пучковой. Определены границы абсо­лютной неустойчивости, рассчитан коэффициент усиления колебаний прп сносовой неустойчивости, сделана оценка критической длины ловушки, при которой рассеяние ионов на колебаниях сравнивается с кулоповскпм рассеянием.

Введение

Неравновесность функции распределения ионов по скоростям в откры­тых ловушках может приводить к развитию микронеустойчивостей. Наибо­лее опасной из них в настояще время считается неустойчивость альфве - новских колебаний, которая развивается на частотах, близких к ионной, циклотронной частоте а)г с инкрементом где р=8лр/#2, Р — давле­

Ние ионов. Колебания с характеристиками, похожими на данную неустой­чивость, наблюдались на установке ТМХ [1]. Возможно, что именно они ограничивали время жизни плазмы в этой системе. В то же время в экспе­риментах на установке ТМХ-11, где для создания термобарьеров исполь­зовались так называемые плещущиеся ионы, плазма оказывалась устой­чивой [2]. Расчеты, подтверждающие возможность стабилизации плазмы в условиях [2], были проведены в [3, 4]. В этих работах, как и в преды­дущих теоретических исследованиях, основные усилия были направлены на определение границ абсолютной неустойчивости, представляющей наи­большую опасность удержанию плазмы в открытых ловушках. Если рас­пределение ионов по питч-углу 0 монотонно в интервале О<0<л/2, т. е. плещущиеся ионы отсутствуют, то условие абсолютной неустойчивости можно представить в виде (ен/е^)2 [5, 6]. Оно отражает анизотроп­ный характер неустойчивости — в соответствии с этим условием уменьше­ние отношения средней энергии продольного движения к поперечной приводит к расширению области неустойчивости. Распределения плещу­щихся ионов немонотонны по углу 0 и характеризуются средним значе­нием этого угла 0 и разбросом 60. Распределение ионов с тем большим основанием может быть названо плещущимся, чем меньше значения 0 (больше амплитуда осцилляций ионов вдоль ловушки) и 60 (острее пик плотности в области остановки ионов). Вполне естественно, что умень­шение 0, приводящее к уменьшению анизотропии распределения (росту отношения вц/вх) Ч способствует стабилизации неустойчивости. В то же время обострение распределения по питч-утлу (уменьшение 60) оказы­вает дестабилизирующее воздействие [3]. Какой из этих эффектов будет преобладать, зависит от конкретных условий экспериментов.

В [3, 4] главным образом анализировалась устойчивость распределе­ний, монотонно меняющихся по модулю скорости V. Между тем на прак­тике популяция плещущихся ионов часто создается посредством моно - энергетической инжекции. Из-за замедления на электронах моноэнергети - ческое распределение имеет тенденцию трансформироваться в монотонное.

Одпако этому процессу может помешать раскачка альфвеновских колеба­ний, способствующая росту 60 и, следовательно, ведущая к устранению популяции плещущихся ионов. Действительно, в [3] отмечено, что рас­пределения, суженные по у, в большей степени подвержены неустойчи­вости, чем размытые.

Настоящая работа имеет целью более детальное изучение неустойчи­вости альфвеновских колебаний для достаточно узких распределений как по питч-углу; так и по модулю скорости. В предельном случае 6У, 60-^0 плещущиеся ионы представляют собой два моноскоростных потока, дви­жущихся навстречу друг другу. Неустойчивость альфвеновских колеба­ний в такой плазме может быть названа скорее пучковой, чем анизотроп­ной. Действительно, как показано в настоящей работе, при 6 У, 60->-О фактор «пучковости» оказывает более существенное дестабилизирующее воздействие, чем фактор анизотропии функции распределения — условие абсолютной неустойчивости приобретает вид рх>0,7* 10~3(ец/ех)г (ср. - с приведенным выше).

Хотя последнее условие является весьма мягким, тем не менее оно может не выполняться в ловушках с большим пробочным отношением, например в газодинамических, где возможно удержание ионов с вц/е ^10*. В этом случае пучковая альфвеновская неустойчивость распадается на две ветви, каждая из которых находится в резонансе с одним из пото­ков, составляющих популяцию плещущихся ионов, (о«(о<±Л||Уц. В систе­мах отсчета, связанных с соответствующими потоками, эти колебания мо­гут развиваться как абсолютные неустойчивости. Однако в лабораторной системе они будут «сноситься» со скоростями ±1>„. Развитие сносовой неустойчивости повышает уровень электромагнитных флуктуаций в плаз­ме, что может привести к усиленному рассеянию частиц и более быстрому разрушению функции распределения, характерной для плещущихся ионов. В настоящей работе произведены оценки уровня электромагнитных флук­туаций и коэффициента диффузии ионов по скоростям, возникающей из-за рассеяния на колебаниях. Показано, что в достаточно длинных ловушках рассеяние на колебаниях превышает кулоновское и может разрушить функцию распределения, характерную для плещущихся частиц.

1. Основные уравнения

При движении ионов по открытой ловушке сохраняются энергия е - —тиг12 И магнитный момент Ц—тш^ Sin2 Q/2B (5), где « — Координата, от­считываемая вдоль магнитного поля. Поэтому в функцию распределения ионов F(V, 0, S) Переменные 0, S Должны входить в сочетании Sin2 0/В (5). Используя это обстоятельство, можно найти функцию распределения ионов в любой точке ловушки.

Принимая во внимание сказанное во Введении, функцию распределения ионов по скоростям в центре ловушки выберем в виде

Если бво<во, то в большей части ловушки вид функции распределе­ния по питч-углу остается гауссовым

+Ep(.(IЈS)-))Ifc!1,

Где 0=aгcsin(Ь,/, Sin 0О), 66=6606'’ Cos 0О(1—B Sin2 0О) B=B0(S)/B0(0)г Ns) =7I0B,/,ц6/66O.

С приближением к точке остановки основной массы ионов (где B(s,) = = 1/sin2 60) разброс по углу и плотность ионов возрастают, а в небольшой окрестности точки остановки (цs//<660 ctg 60,1 — характерный масштаб из­менения магнитного поля в окрестности точки остановки) распределение отличается от гауссова:

"о Ъ* I (0—л/2)4 Т7Ч

/(М)= ,Wsin9 "Pi“ 466/ Ctg2 В» )6{V-V)-

Из этой функции распределения находим два важных параметра — макси­мальную плотность ионов П =ЧгП0Т{Чк) (cos 6O/(2Jiц6O sin3 6О))'А и макси­мальный угловой разброс 66*~(2660 Ctg60)' Которые понадобятся в даль­нейшем для оценок.

Рассмотрим электромагнитные колебания, распространяющиеся вдоль магнитного поля ловушки (Дx=0, Кл>0). В плазме с функцией распре­деления ионов (2) они описываются следующим дисперсионным уравне­нием:

■ -КГ-ТпИ-5Г (l+lW2(>.№.+,->r_» +

(IP++W-)-—}-0, (3)

M.- J

6 Skv± d

Где ^±=^(2±), W — Интеграл Вероятности От Комплексного Аргумента, Z±e((D—G)<±fcv„)/66Fcv_L, VW=v cos 6, V±=v sin 6. В гидродинамическом при­ближении (|Z±|»L) Дисперсионное уравнение принимает вид

А

2 (Д2-Л2РИ2)2 &2Рп2(Д2—&2Р,|2) ’ К }

Где Рі|=У||/(0І, Pj., И = (0рі2Ух,2||/(0<2С2, Д=(а)і—(O)/(Dt.

2. Абсолютная неустойчивость

По характеру развития различают абсолютные и сносовые неустойчи­вости. При выяснении характера неустойчивости альфвеновских колеба­ний будем по отдельности рассматривать область, далекую от точки оста­новки плещущихся ионов, и ее малую окрестность. Первая область харак­теризуется малым разбросом ионов по продольным скоростям. Выяснение характера неустойчивости в этой области можно проводить в гидродина­мическом приближении, используя дисперсионное уравнение (4). Это уравнение удобно представить в виде

2) =Р’+Р‘ (1-2^) +Р (*» (*4-1) +*о) -**о=0, (5)

Где Р=2(кр„П$±, *=Д (2/рх)*, о=М2/рх)*-

Для анализа характера неустойчивости следует найти точки ветвления решений соответствующего дисперсионного уравнения Л (со) и на плоскости комплексных значений со определить их положение относительно контура 1шЛ(о))=*0. Согласно [7] неустойчивость будет абсолютной, если выпол­няются следующие условия: 1) найдется точка ветвления <ов, расположен­ная в верхней полуплоскости и лежащая между контуром 1Т&(а>)в0 и осью 1Та)=0; 2) корни дисперсионного уравнения, совпадающие при. (о=©., приобретают различные знаки 1Т К, если 1Т со-**<*.

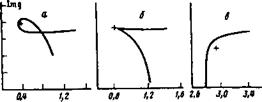
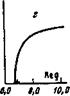
Результаты численного исследования изображены на рисунка. Точка ветвления корней (5), определяемая системой <2>=0, 5>р'=0, отмечена крестиком. Из рисунка следует, что, как и требуется условием 1, точка ветвления располагается между контуром 1Т £=0 и действительной осью. Однак« в момент стягивания петли на этом контуре она попадает на него. При соответствующем значении о абсолютная неустойчивость раскачивает­ся на колебаниях с 1т&=0 [7]. Численное исследование показало, что выполняется и второе условие абсолютное неустойчивости (см. выше).

Критическое значение параметра о, при котором точка ветвления вы­ходит в верхнюю полуплоскость, оказалось равным оег~404,6. Соответ­ственно условие раскачки абсолютной неустойчивости приобретает вид Рх>8/овг1(ей/ех)1«0,725*10-3(е11/ех)2.

Критическое значение о может быть получено аналитически. В силу того, что коэффициенты уравнения (5) действительны, точка ветвления

Зсожет сойти с действительной оси на плоскости комплексных значений G Только через слияние с комплексно-сопряженной точкой ветвления. Для определения оег, при котором осуществляется слияние, необходимо к двум уравнениям £Ю=0, 2)Р'=0 добавить третье 2)РР"=0. Совместное решение этой системы приводит к значению Оег = 7+2У58 Cos (1/3 Arccos (433/58*)). Следует отметить, что в исходном уравнении (5) отсутствуют как боль­шие, так и малые параметры, и поэтому сравнительно большое значе­ние Оег является результатом «игры чисел».

При малых значениях о неустойчивость теряет «пучковый» характер, переходя в «анизотропную». В этом случае для частоты колебаний, раска­чивающихся как абсолютная неустойчивость, имеется простое приближен­ное выражение A. s«(Я_L/2),/*Јe, Где Ga^i—Еы/к(3а)ч>.

Оценим, применим ли результат расчета границы области абсолютной неустойчивости по гидродинамическому уравнению для распределений вида (2). При о<1 характеристики абсолютно неустойчивых колебаний, найденные из (5), таковы (g*^i, Рл~(—1О/З)7*)» что условие гидродина­мического приближения выполняется автоматически z±'^vja'*6v^i. Если параметр о лежит в интервале 1<о<оСг то, как показывают числен­ные расчеты, величина |z±|~i>„/6I>n Также велика по сравнению с единицей.

Параметр о уменьшается при движении от центра ловушки к точке остановки плещущихся ионов. Поэтому по отношению к раскачке абсо­лютной неустойчивости наиболее опасна область, в которой скорость про­дольного движения мала по сравнению со скоростью в центре ловушки рпо, но еще значительно превышает разброс 6Уц. Заменяя в выражении для о величину у,, на 6Уц, приходим к следующему условию раскачки абсолютной неустойчивости:

Я*»10“366*

Или в другом виде:

Яo>4O“360ol/t cos^Oo/sin'7*©#. (6)

В малой окрестности точки остановки плещущихся ионов, где ув^6Уц, наличие средней скорости у потоков плещущихся ионов несущественно, и в качестве приближенного условия абсолютной неустойчивости можно использовать полученное в [5, 6] Яj_^ (вн/вJ_)*. Его можно представить в

Виде р*^60* т. е. оно является более жестким по сравнению с полу­ченным выше (см. (6)).

3. Сносовая неустойчивость

При отсутствии абсолютной неустойчивости в плазме с плещущимися ионами может развиваться сносовая. Она существует вблизи резонансов А=±Лрц (см. Введение). Полагая Д=±/:р„-Ьб, |б|<Лр„ из (4) для б по­лучаем выражение

. ... Р„*(Р„2-4Р„АТ’

4Д2

Неустойчивыми оказываются колебания IA|>Am<N=,((V/4P_L)V Максималь­ный ИНКреМеНТ Max A)IVPj_/2 В У2 раз меньше, чем в плазме без направ­ленных потоков плещущихся частиц, так как здесь в резонансном взаимо­действии с волной участвуют лишь ионы, движущиеся в ту же сторону, что и колебания; их плотность составляет половину от общей плотности ионов.

При увеличении расстройки А перестает выполняться условие гидро­динамического приближения и неустойчивость стабилизируется. Условие стабилизации можно найти, приравнивая нулю по отдельности действи­тельную и мнимую части (3). Например, для колебаний, находящихся в резонансе с потоком, движущимся направо, из мнимой части (3) имеем ——б©(о/&у_|_. Учитывая, что |Z+|»L, Из действительной части получаем А«о)р,/У2сб0 и, следовательно, Дта*да(P„/2)V,/60. Сравнивая полученные условия неустойчивости Am,N<A<Am«, Приходим к выводу, что неустой­чивость существует при выполнении условия P_L>664. Это условие можно также представить в виде

В >ЛЙ * С08’е° Ь*

Р° ’ sin20о (l-ism2©,,)*

(ср. с (6)).

Сносовые неустойчивости характеризуются коэффициентом усиления

А =ехр г. Г - 1(7/^)*,,,. |2 — границы зоны усиления.

*T

В открытых ловушках магнитное поле нарастает от центра к пробкам. Наибольший коэффициент усиления будут иметь колебания, для которых условие |A|=Amtn Выполняется в центре ловушки. Если магнитное поле зависит от продольной координаты по параболическому закону B(S) = E2?0(L+S*/.Ј2), То величина Г дается выражением

L В,,Соз*е.

2Р0 Н° Sin2 0О ’

Где ^=| Dhh(L—H)'!'(H—Л0)“7 Ло = зт20О, Л=6Зт20О;

N.

Р0 — ларморовский радиус ионов, рассчитанный по полной скорости, Hmax Определяется из уравнения

■ H ^ = (Ро/2) 4l sin2 0o/60o cos'/j 00. (7)

(1—Л)

Если зависимость магнитного поля от продольной координаты близка к прямоугольной с резкпм возрастанием магнитного поля в области про­бок, то для величины Г имеем следующую приближенную оценку:

Г » — Ро7’ Tg 00,

Ро

Где L — теперь длина ловушки.

2 Физика плазмы, вып. 5 545

В настоящей работе не рассматривались явления, развивающиеся в окрестности точки циклотронного резонанса. При приближении к этой точке К-+ 0. Однако точка циклотронного резонанса не яиляется простой точкой отражения, так как в ней сливаются две ветви колебаний, соот­ветствующие двум решениям дисперсионного уравнения (4). Ситуация еще более усложняется, если, как это обычно бывает, в ловушке наряду с плещущимися присутствуют холодные ионы. Резонансное взаимодействие с холодными ионами приводит к поглощению колебаний. Тем не менее и в этом случае коэффициент отражения колебаний от точки циклотронно­го резонанса может быть отличен от нуля. Если он достаточно велик, то неустойчивые колебания Ь)>ь)<t mm, Для которых имеются две точки цикло­тронного резонанса, могут стать собственными. Развитие же неустойчивых собственных колебаний эквивалентно абсолютной неустойчивости. Остав­ляя изучение этой возможности на дальнейшее, в настоящей работе огра­ничимся колебаниями Ь)<ь),, m,„ Для которых точки циклотронного резо­нанса отсутствуют.

4. Коэффициент квазилинейной диффузии

Оценим коэффициент диффузии ионов по скоростям, вызываемой рас­сеянием на колебаниях. Для этого сначала найдем уровень электромаг­нитных флуктуаций в плазме. Источником колебаний являются левопо­ляризованные микротоки; их спектральная плотность равна [8]

<|/+|г>>.. = - * 1 Dv 1 (v)V±b(ш—й)(—ЛцРц), (8>.

Здесь считается, что К±Р±<1. Используя (8) и уравнения Максвелла, на­ходим спектральную плотность затравочных альфвеновских колебаний

<|Е+1^|г JDvv±‘j(v) |;

Здесь ЗЬ — левая часть дисперсионного уравнения (3) или (4), определяю­щего собственные колебания. Коэффициент усиления колебаний при про­хождении ловушки был рассчитан выше. По усиленному уровню флук­туаций найдем квазилпнейный коэффициент диффузии

D (wii) — J <Яс Da> {е/т) 2< | Е+1 Г>»,„6 (со—АгцУ,) = F Л 4n*W Лг(1С) F

APa/(v)‘

Интеграл по Кп можно оценить, разлагая ЗЬ по W Вблизи частоты собственных колебаний:

Dk>> 1 F Dkw 2Д&„

&2 (Я)»')2'’ (Иесо-с(ъФш’УК

О'/, о '/.

-1.

(а)^)«/)2М0 ’

Отсюда же следует, что

Интеграл по К± оценим из следующих соображений. При распростра­нении колебаний под углом к магнитному полю (к±¥= 0) неустойчивость ослабляется: 1т&ц-*1т &ц(1—(Лх1;х/2С1>)а). Ввиду экспоненциальной за­висимости А от 1т &ц величина А резко спадает с ростом К±. Характерный масштаб ДК± (ширина спектра) определяется условием IТкпгтахСк±У±/ /2А))2<1, откуда находим ДЛ^_2—б©‘/я (р,,/^) Таким образом,,

Получаем оценку коэффициента диффузии

В у ^ ..Лг Ь* 6д у. С08*6« (9ч

П1 Ь^' пЛ ро';' " СО8,/!0 '

Амплитуда колебаний зависит от расстояния вдоль магнитного поля. Усреднение коэффициента диффузии по этой координате дает дополни­тельный множитель (1т ^2««*)"'. В результате находим

В -.<» М’р° ае.*008*6.

" Р.»віпЄ.(1-Л. м.),/‘ ’ < '

Где величина Лт*. определяется соотношением (7).

Выражения (9), (10) получены в предположении параболической за­висимости магнитного поля от продольной координаты. Если данная за­висимость имеет вид прямоугольной ямы длиной Ь, то

_0^р 69»

D-A

Rilf Яsin0

Эффективный коэффициент диффузии под действием кулоновских - столкновений можно приближенно представить в виде Z)c~a)P,4/rti;602. Вви­ду экспоненциальной зависимости Dav От параметра ЫР в достаточно длин­ных ловушках рассеяние на флуктуациях будет преобладать над кулонов - ским. Например, при Я—0,01, 60о—0,01, Ь)p,/ь)~10, Sin0~O, l В ловушке с профилем магнитного поля вида прямоугольной ямы условие £)«*>/)* вы­полняется при L/p^2 103.