ФИЗИКА ПЛАЗМЫ

ЛУЧЕВЫЕ ТРАЕКТОРИИ ЭЦ КОЛЕБАНИЙ В ОТКРЫТЫХ ЛОВУШКАХ

ЗВОНКОВ А. В«, ТИМОФЕЕВ А. В.

1. Распространение электронных циклотронных колебаний, как пра­вило, с хорошей точностью описывается лучевым приближением. Иссле­дование лучевых траекторий высокочастотных волн в магнитных ловуш­ках позволяет дать ответ на ряд вопросов, в частности о реализуемости того или иного резонанса и о месте выделения энергии при нагреве. Из­вестно, что электромагнитные электронно-циклотронные колебания испы­тывают циклотронный резонанс (их волновой вектор обращается в беско­нечность) лишь в том случае, если они подходят к поверхности о, (г) — й> (а), — электронная циклотронная частота) с волновым вектором К||В0. Д. т этого необходимо, чтобы в точке пересечения лучевой траектории с резо­нансной поверхностью выполнялось условие VBo||Bo [1]. В открытых ло­вушках оно выполняется лишь на их оси. В остальных случаях волновой вектор на резонансной поверхности остается конечным, а правополяризо­ванная составляющая электрического поля волны падает до величины порядка (VTJc)E, где ут. — тепловая скорость электронов, £ —полное электрическое поле волны. Это ведет к ослаблению резонансного цикло­тронного взаимодействия. Однако при VB0 JT В0 Колебания могут испытать плазменный резонанс вблизи поверхности А),(г)=а). Действительно, усло­вие плазменного резонанса имеет вид

Е, sin* 0+е* cos2 0=0, (1)

Где со2), е3=1—о)*.2/«2, о)Р, — электронная плазменная

Частота, 0=кВо. Разрешая (1) относительно ои, можно убедиться, что одна из двух резонансных частот стремится к ои, при 0->-О. Поэтому на первый взгляд кажется, что циклотронный резонанс может рассматриваться как частный случай плазменного. Оказывается, что исследование лучевых траекторий проясняет и этот вопрос.

Траектории электронных циклотронных колебаний в открытых ловуш­ках изучались численно в [2—4]. Ниже наряду с численным анализом используем также аналитический подход работ [5, 6], где рассматрива­лись лучевые траектории верхнегибридных колебаний в неоднородной плазме.

Из результатов упомянутых работ следует, что для того, чтобы соста­вить обще^ представление о ходе лучевых траекторий, достаточно рас­смотреть их поведение вблизи особых точек. В нашем случае такой точкой является пересечение поверхности со* (г) “СО с осью ловушки.

2. Дисперсионное уравнение высокочастотных (а)~а),) колебаний хо­лодной плазмы имеет вид (см., например, [7])

Бж(в! sin20+e, cos2 0)iV4-h ((е,2г—в!2) sin2 0—

—tits (l+cos2 0) )N2+ (e,2—ei22) е3в0, (2)

Где е,2**а)р.2а)*/(1)(а)2—со,2), N — показатель преломления. Так как ниже Оудут рассматриваться лучевые траектории вблизи особой точки — точки пересечения поверхности 0).(г)**0) с осью ловушки, возможны некоторые упрощения.

Во-первых, вблизи особой точки сильно возрастает iV„ (в этом убедим­ся ниже), поэтому в дисперсионном уравнении (2) оставим лишь наи -

Большие слагаемые и приведем его к виду

/)«^2(е1^хг+е, Л^112-2е1ез)=0. (3)

Во-вторых, для упрощения анализа вместо системы с цилиндрической симметрией рассмотрим плоскую, силовые линии магнитного поля будем считать прямыми, параллельными Ог. Неоднородность магнитного поля учтем лишь в зависимости величины магнитного поля от координат, которую, очевидно, можно выбрать в виде

В(хч г)=Вов(+г/Ьц+гх21Ьлг).

Здесь начало координат выбрано в особой точке, а)=еВ0в1тсч е—=Н. При е=1 координатная зависимость магнитного поля вблизи особой точки со­ответствует открытой ловушке с пппВ, а при е=—1 — центральной части аксиально-симметричной ловушки.

Положим теперь в (3) е1«о)Ре2/2а)(а)е(г)--а)), а)Р,«соп81 и введем без­размерные переменные |=х/р, гДе р=£„а)Р«2/

У2а)2е3. Умножив (3) на резонансный знаменатель а)в(г)—ои, приведем дисперсионное уравнение к виду

Л=/)С(а).(г)-а)) = (^а§2)^2+^2-9=0, (4)

Где

А=е (£ц/Ь±) 2а)ре2/2а)2е3, д= (а)1/„/с)2а)Р.4/2а)4е3,

€ — несущественная константа.

Лучевые траектории, определяемые уравнением (4), при д=0 совпа­дают с характеристиками уравнения Пилия — Федорова [5, 6]. В [5, 6] анализировались также и лучевые траектории, описываемые дисперсион­ным уравнением вида (3). Приведем упрощенный вариант анализа.

Рассматривая Л как гамильтониан, РС — как компоненты импульса,

?, 5 ~ как координаты, а также переопределяя время в соответствии с со­отношением -рьг(т;)с11с1т-+с11с1т, где т=(о£, получаем

1—2 р{/р:г,

2а%,

(5)

6—2(5+а6*)/л,

А—1-

Эту систему можно получить из (2), (3) и стандартным способом, если учитывать лишь наибольшие — резонансные — слагаемые.

Последнее уравнение системы дает Рц=т. Из двух первых легко полу­чить

4а Р» + -^гЛ-0.

Решения этого уравнения имеют вид

^=Л+тт*+Л_тт-,

1/1 *

Где А± — произвольные постоянные, К* в "2~^ “]£—^а/ » При

А>‘/1в решение удобно представить в виде

Р1—АоТ!* соз (Ф (т)),

Где Ф (т)*61п т+Фо, б—(4а—1/*),/', А0, Ф0 — произвольные постоянные. Величину | находим из второго уравнения:

£ - |чЛ+‘г+тт-,+Л_'г-тт-1) при а<*/„,

5=Л0(ат)"'лсоз (Ф(т)Н-фо), ф0=агс1826 при а>71в -

4А+А-Х, A<‘/,.F

/ 1 Mfia—IV*

Іяждт-*—А9гі1+-^саа2Ф-------------------------------- зіп2Ф, a>f/ie.

Из полученных выражений следует, что вне зависимости от значения па­раметра А существует выделенная траектория, идущая вдоль оси |=0 в точку £=0 (Л±=0 при a<Vie, Л0=0 при a>7ie). На этой траектории осуществляется циклотронный резонанс. Однако данная траектория не­устойчива. Поведение траектории общего вида (А±¥*0 или А0¥*0) сущест­венно зависит от значения А (рис. 1). Если а>0 (магнитное поле подобно полю открытой ловушки с min В), то лучевые траектории при стя­

Гиваются к особой точке (0,0). Причем при a<‘/ie зависимости §(т), £(т)г начиная с некоторого момента времени, становятся монотонными. При а>7іб процесс приближения к особой точке имеет колебательный харак­тер. В [5, 6] такие особенности были названы узлом и фокусом соответ­ственно. При а>0 траектории подходят к особой точке со стороны £<0, Т. е. ДОЛЖНЫ пересечь поверхность 0)е (г) =0). При подходе к особой точке К-*-Оо, 0—*0, а групповая скорость перпендикулярна основному магнитно­му полю. Последнее обстоятельство свидетельствует о потенциальности колебаний. Действительно, из (1) получаем kV, rcokdZ)/dk=2Z)=0. Таким образом, на траекториях общего вида (А±Ф0) осуществляется плазмен­ный резонанс, и в силу потенциальности колебаний в малой окрестности особой точки вектор электрического поля колебаний направлен вдоль ос­новного магнитного поля (Е||к||В0).

Таким образом, в магнитном поле ловушек с min В циклотронные колебания испытывают плазменный резонанс в особой точке (0,0), лежа­щей на поверхности циклотронного резонанса со* (г) =со. Однако этот резо­нанс отличается от обычного циклотронного. Последний реализуется для лучей, распространяющихся вдоль оси (Л±=0). Такие колебания сущест­венно непотенциальны (E-Lk) и в противоположность потенциальным приближаются к особой точке со стороны большего магнитного поля.

Если а<0 (центральная часть аксиально-симметричной ловушки) г то лучевые траектории общего вида (Л±=Иї0) при т-><» уходят на беско­нечность, асимптотически приближаясь к параболе £=— (а/ч+)|2. По тер­минологии [5, 6] особая точка в этом случае является седлом.

В проведенном анализе* считалось, что (о>(оР, (е3>0). Это предполо­жение соответствует условиям большинства современных экспериментов по ЭЦР нагреву плазмы в открытых ловушках. При (i)pe>co знак величи­ны А меняется. Поэтому при высокой плотности плазмы в ловушках с min В лучевые траектории отталкиваются от особой точки (0,0), а в ак­сиально-симметричных ловушках притягиваются к этой точке.

3. Нами проводился также численный анализ лучевых траекторий в ловушке с min В на основе уравнения (2). Магнитное поле определя­лось потенциалом (B0=V%) х(г) = ^(2)~(7*2/^) V”(Z)+R*G Cos 20, где F(z)=z-bЈ7iz3, G—Сг, зависимость плотности от координат бралась в виде N0(R)=No ехр ( — (г2+гг)/1г). Параметры задачи соответствовала экспери­ментам по созданию и нагреву плазмы в установке ОГРА-4: =0,503-10~3 см“2, С2=0,103 см”2, /=10 см, a>/w.(0)-l, 2, ь)p.(0)/(o=0,302, (0=2,35* 10і* рад/с. Расчеты лучевых траекторий в холодной плазме под­твердили проведенный выше анализ (рис. 2). Однако учет затухания ко­лебаний, обусловленного конечностью температуры электронов, показал,, что если Т,^ 10 эВ, п^Ю12 см'3, то колебания практически полностью поглощаются уже при первом пересечении поверхности циклотронного резонанса. Таким образом, довольно сложная часть траектории, располо­женная в области 0>,(г)<(|>, может быть реализована лишь на начальной стадии создания плазмы.

Подводя итоги настоящей работы, отметим, что она основана на ис -

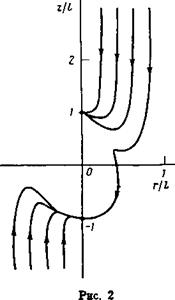Рис. 2. Лучевые траектории в ло­вушке с min В при 0=0. Траек­тории стягиваются к точкам цик­лотронного резонанса на оси ло­вушки (резкий поворот одной из траекторий происходит на по­верхности верхнегибридного ре­зонанса ь)=((i),2 + (ьp,2),/>)

Пользовании аналогии между лучевыми траекториями электронных цик­лотронных колебаний в холодной плазме, помещенной в магнитное поле адиабатической ловушки, и траекториями верхнегибридных колебаний в неоднородной плазме, исследованными в [5, 6]. Показано, что цикло­тронный резонанс (&-><», E-Lk) осуществляется лишь на выделенной, не­устойчивой траектории, идущей вдоль оси ловушки. При распространении по траекториям общего вида колебания превращаются в потенциальные (к-+оО, ЕЦк). В ловушках с min# траектории потенциальных колебаний стягиваются к точке циклотронного резонанса на оси ловушки. При этом осуществляется плазменный резонанс колебаний с В аксиаль­

Но-симметричных системах траектории «отталкиваются» от этой точки.