Явление авторезонанса при электронном ЦИКЛОТРОННОМ НАГРЕВЕ ПЛАЗМЫ
А. И. Нейштадт, А. В. Тимофеев
Показано, что явление авторезонансного ускорения может играть важную роль в электронном циклотронном нагреве плазмы. По-видимому, оно ответственно за образование кольца высокоэнергичных электронов при электронном циклотронном резонансном нагреве плазмы в открытых ловушках и бампи-торах. Найдено также, что авторезонанс - ные эффекты могут ослабить нагрев основной массы электронов, удерживаемых в магнитных ловушках.
Введение
Действие ряда ускорителей заряженных частиц основано на явлении авторезонанса (автофазировки), т. е. автоматического поддержания условия циклотронного резонанса при медленном изменении параметров системы. Так увеличение магнитного поля или уменьшение частоты ускоряющего ВЧ поля влекут за собой рост энергии частицы в соответствии с резонансным условием (й—<йе°тс2/г. Здесь е — энергия частицы (для определенности рассматриваются электроны), ю — частота ускоряющего ВЧ поля, <йв°=еВ01тс — циклотронная частота, рассчитанная по массе покоя электрона, Во — индукция магнитного поля.
В большинстве плазменных ловушек магнитное поле стационарно а для ВЧ нагрева плазмы используются колебания фиксированной частоты. В этих условиях авторезонансное ускорение становится возможным вследствие неоднородности магнитного поля ловушек, при движении заряженных частиц в сторону возрастания магнитного поля.
По нашему мнению, с авторезонансным ускорением связано появление^ группы высокоэнергичных электронов (е—Тс2^100 кэВ) при электронном циклотронном резонансном (ЭЦР) нагреве плазмы в магнитных ловушках. В исследованиях, проведенных на открытых ловушках и бампи-торах, обнаружено, что эти электроны образуют кольцевой слой, расположенный вблизи пересечения резонансной поверхности ((0 = Й)в(г)) с Поверхностью минимумов магнитного поля на силовых линиях ((В0У)В0= =0), см., например, [2—4].
В настоящей работе показано, что если условие циклотронного резонанса выполняется в точке минимума магнитного поля на некоторой силовой линии, то электроны, движущиеся вдоль этой силовой линии с достаточно малой скоростью, особенно легко «захватываются» в авторезонанс. При этом они локализуются в окрестности точки минимума магнитного поля. Под действием низкочастотных колебаний, которые практически всегда самопроизвольно возбуждаются в магнитных ловушках, авто - резонансные электроны должны дрейфовать поперек магнитного поля. Дрейф в сторону большего поля сопровождается ростом их энергии. В результате вблизи той части поверхности (В0У)В0=0, где й)е°>(о, образуется слой высокоэнергичных электронов. Геометрия магнитного поля открытых ловушек и бампи-торов такова, что этот слой должен быть кольцевым.
•> Плазменная ловушка с нарастающим во времени магнитным полем, помещенная в электромагнитное ВЧ поле — плазмепнып сиыхротрон,— исследовалась В [1].
При достаточно большой амплитуде ВЧ поля явление авторезонанса влияет и на ЭЦР нагрев основной массы электронов, свободно осциллирующих вдоль неоднородного магнитного поля ловушки. Если такой электрон, движется в сторону большего поля, то при прохождении зоны электронного циклотронного резонанса он может «захватиться» в авторезонанс. Однако процесс авторезонансного ускорения обратим и электрон будет отдавать энергию ВЧ полю при обратном движении в сторону меньшего магнитного поля. Результирующее изменение энергии равно нулю с той точностью, с которой сохраняется адиабатический инвариант, характеризующий состояние авторезонанса (см. ниже основной текст статьи). Существенно, что захват электрона в авторезонанс сопровождается на фазовой плоскости переходом траектории через сепаратрису, разделяющую области финитных и инфпнитных траекторий. Такие переходы приводят к изменению адиабатического инварианта (см. [5—7]). Согласно [6—8], при многократных - прохождениях через зону циклотронного резонанса изменения адиабатического инварианта, а вместе с ними п изменения энергии движения электрона поперек магнитного поля, е^ц, оказываются некоррелированными. (Здесь 1=р±212ть}е° — величина, являющаяся адиабатическим инвариантом в отсутствие ВЧ поля.) Следовательно, должна возникать диффузия по ц. Коэффициент диффузии уменьшается с ростом амплитуды ВЧ поля[82]: Д
В случае слабого ВЧ поля, когда новый адиабатический инвариант не возникает, (см., например, [11]). Таким образом, должно сущест
Вовать оптимальное значение амплитуды ВЧ поля, при котором коэффициент диффузии максимален и, следовательно, ЭЦР нагрев происходит с наибольшей эффективностью. В настоящей работе дается оценка оптимального значения Е.
1. Поперечный адиабатический инвариант в присутствии ВЧ поля
Движение электрона в стационарном магнитном поле в присутствии ВЧ колебаний описывается гамильтонианом (см., например, [12])
Я=е —цй)+*(2ес50]и),/,(еЛ/е)со8 Ф. (1)
Здесь пспользованы обозначения
Е = [ (тс2)2+2есв0х+{рцс)2]'11
— энергия электрона, А — амплитуда вектор-потенциала ВЧ поля, Ф=* =0—й)£, 0 — фаза ларморовского вращения электрона. Рассматривается простейший случай колебаний с й)«й)е, правой поляризацией вектора электрического поля и длиной волны в направлении поперек магнитного поля, значительно превышающей ларморовский радиус электронов, эффект Доплера не учитывается. В (1) канонически сопряженными переменными являются ц, Ф и Рь ъ, Где 2 —Координата вдоль стационарного магнитного поля. Каноническое преобразование фазы 0-*-Ф=0—ю* привело к появлению в (1) второго слагаемого.
Обычно за время прохождения электрона вдоль ловушки фаза Ф успевает измениться на величину, много большую л, поэтому переменные ц, Ф можно считать быстрыми, а р(|, Г — медленными.
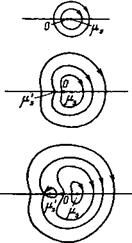
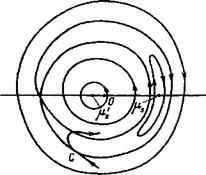
Картина фазовых траекторий на плоскости быстрых переменных при заданных значениях медленных изображена на рис. 1. При ©/<© фазовые траектории близки к окружностям с центром в точке (ця«(еЛ)2й)/
|
Быстрое движение по фазовой плоскости (ц, Ф) характеризуется адиабатическим инвариантом I— фц^Ф - В области используя выражения Для адиабатического инварианта нелинейного маятника (см., например, [5]), получаем /=2л^,±8у1,,х^(х“'1), (4) /=16у,,*[£(х)+(х2-1)А'(х) ], Где К, Е — полные эллиптические интегралы, К=(1и12и)1'*, ш=(Я0—Я+р)/ /2а, 1;=вР/2а. Верхнее выражение (4) следует использовать для траекторий, охватывающих начало координат, на которых фаза Ф меняется неограниченно, нижнее — для траекторий с ограниченным изменением Ф. По аналогии с нелинейным маятником первый режим движения будем называть вращательным, второй — колебательным. Соотношения (4) выражают I в виде функции от со,0(г), Рь х(со,°, рв, И). Если с помощью (4) найти обратную зависимость //[со/(г), рп, *(со/(г), /)], то получим гамильтониан, описывающий медленное дви Жение вдоль магнитного поля, усредненное по быстрым (поперечным) осцилляциям, Я-Я.(г, Л)+р[ 1-2х2(г, Ръ /)]. (5) |
|
72е* (со/—со)2, О), см. рис. 1 ,а. Здесь ^ со/=со.(е‘), е*=[(тс2)2+(р11с)2],/а. С увеличением со/ фазовые траектории «поджимаются» слева, и при со/= всо[1+3(е4/е*)*/2] рождается новая стационарная точка (ц/«(е*/ /2ш) {еА/г*)Чг, л) см. рис. 1,6. Придаль- А нейшем увеличении со/ область, заня Тая траекториями, окружающими точку (ц/, л), расширяется, а сама эта точка приближается к началу координат. Одновременно стационарная точка 6 (ц„ 0) смещается в область больших Значении ц (см. рис. 1,в, Г). Так, при ©/—со>со (еА/е*У* имеем |
|
2е‘ (й)/ со)2 Авторезонансное ускорение испытывают электроны, движущиеся по орбитам, окружающим точку (ц„ 0). Если со/—со>со (еА1ъ*У то в области ц&цв гамильтониан (1) принимает вид //«#0(р|„ 2)-а(ц-ц.)2+Рсо8Ф, (2) |
|
(еАУ И. *-------------- |
|
Яо(р,„2) |
|
Тг Т" |
|
2т со,0 ’ (3) А=со3/2со,°тс2, Р=(есоЛ/с) (2цв/тсов°)'л. |
|
(—+А-) 'со (де ' |
|
Г' 2со/ |
|
И« |
|
Тг-'1 |
|
|
|
|
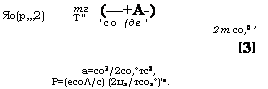 |
|
|
Установим условия, при которых существует адиабатический инвариант /, т. е. продольное движение является медленным по сравнению с поперечным. Электрон осциллирует вдоль магнитной ловушки с так называемой баунс-частотой (&ь~р\1тЬ0, £0 — характерный масштаб изменения магнитного поля. Когда электрон находится вдали от точки циклотронного резонанса Г, (<о.(2«)=й)), условие адиабатичности имеет вид |шв—о)|>шах(|оэв|,/1| |со«|1/1). (Величина ю, обращается в нуль, если электрон останавливается в точке циклотронного резонанса или если последняя совпадает с точкой минимума зависимости юДг).) Приведенное условие очевидным образом нарушается при попадании электрона в резонансную зону, где о),«©. Однако движение остается адиабатичным и в этом случае, если частота поперечных осцилляций под действием ВЧ поля Q значительно превышает тах(|<Ь«|у>, |о).|7*). Используя (1), (2), находим
(Ер±/В0тс)'и. Ебли точка 2« смещена достаточно далеко от точки минимума магнитного поля (й),(г,)— м., ТО<„^Й), то условие адиабатичности имеет вид
В о I Ья(о р± ' Ь,(й' ' Тс’ >
Здесь оценка величин ю«., ю, проведена с помощью гамильтониана П^Н0 (см. (5), (3)):
|Й'1<й~ръ/тЬ,(й, |ше/ш|~(р±/тЬ,(д)г1
Где
£«=| (^й)/^г)/й) |х-1хв.
При й)в(г8)— (ав, движение аднабатично, если
С у/» Р*
В0 ' Ь0(й' р±(тс)ъ ’
Здесь использована оценка |со«/со| — {рц/тЬою)1, где
£,=» | ((Ра>/<1гг) /2<о |
2. Нагрев при движении вдоль магнитного поля
А) Рассмотрим движение электрона, поперечная компонента начального импульса которого достаточно мала: Р±о1тс<.(Е1В0)"*. Предположим, что в начальный момент Электрон находился в области, где ю>©,. В силу сохранения адиабатического инварианта рассматриваемые электроны будут всегда двигаться в малой окрестности стационарной точки (ц„ 0), см. рис. 1. Поэтому их движение может быть описано гамильтонианом
(Рн» «е,-ц, й)+ (2ЕсВ01,)еА/е„ (8)
Где
Е,=[ (/ис^+ЗесВои.+^с)2]1'.
А ц, определяется условием (дН/дц) фа_о=0.
Продвижение электрона в область большего поля сопровождается ростом а следовательно, и диамагнитной силы, выталкивающей элек
Трон в область слабого магнитного поля Р=—1ЕсВ0'/е. Максимальное значение (4 зависит от продольной компоненты начального импульса.
В слаборелятивистском случае из (8) получаются простые выражения для Цта*- Так, если Ро\1тс<(Е1ВоУ то электрон отражается от области большего магнитного поля (магнитной пробки), не доходя до точки циклотронного резонанса, при этом Цтвг® (/?,|о72то3с2(й){Во/Е)г (р±Т«/Тс~(о/ !тс)гВ01Е). Если р,]0/тс> (£/£<>)"*, то Цт^Рнос/а (р^п, ах1тс&(2рЛ0!тс)Чг, Схтпв*«(2е||0тс2),/1). Однако рассматриваемые процессы обратимы — после отражения от магнитной пробки они протекают в обратном порядке. В результате ц возвращается к своему первоначальному значению ц0.
Таким образом, если в случае слабого ВЧ поля электрон, проходя через область циклотронного резонанса, получал конечное приращение энергии ДГ<*>Е (см., например, [11]), то при выполнении условий (7), обеспечивающих существование поперечного адиабатического инварианта, результирующее приращение энергии оказывается равным нулю.
Предположим теперь, что электрон с Р±1тс<&(Е1В0У1* в начальный момент находился в области сильного магнитного поля (©/—©>©(еЛ/©/)*). Такие электроны на фазовой плоскости располагаются в окрестности стационарной точки (1*/, л). При смещении электрона в область слабого поля точка (ц/, л) сближается с гиперболической (см. рис. 1). После их слияния рассматриваемые электроны оказываются на фазовой плоскости на некоторой орбите, охватывающей точку при этом Р±~тс(Е1В0)ч‘. Когда электрон возвращается в область сильного поля, то вероятность оказаться в месте рождения новой стационарной точки, т. е. иметь Ф=лг пренебрежимо мала. Поэтому с вероятностью Р« 1 электрон останется на орбите, охватывающей точку (ц,, 0), и соответственно будет иметь Р±~ ~тс(Е1В0Уи.
Б) Рассмотрим электроны с Р±/тс^(Е/Во)41 и предположим, что при движении вдоль неоднородного магнитного поля они заходят в область, где выполняется условие (©/—©)>3/а©(вЛ/ев)*. Фазовые траектории таких электронов на плоскости (ц, Ф) могут пересечь сепаратрисы, разделяющие области вращательного и колебательного движения. В соответствии с [5—7] переходы фазовой траектории через сепаратрису должны приводить к изменению адиабатического инварианта на Д/</. В настоящее время развиты методы, позволяющие рассчитать ДI при линейном во времени изменении параметров системы. В рассматриваемой задаче определяющей является временная зависимость величины ©.[2(0]~ ©. Ее можно считать линейной, если точка циклотронного резонанса удалена как от точки минимума ©.(г), так и от точки остановки электрона (рц=0).
Величина ДI существенно зависит от значения фазы Ф, при котором происходит переход через сепаратрису. По этой причине при неоднократных переходах процесс изменения I принимает случайный характер [6-8].
Простое выражение для ДI удается получить в области и>(тпсг/ /©) (Е/Во)* ((р±1тс)^>(Е/Во)'и), где картина фазовых траекторий на плоскости (ц, Ф) близка к фазовому портрету нелинейного маятника (см. рис. 1). В этой области не все электроны захватываются в колебания при прохождении через точку циклотронного резонанса. В предположении равномерного распределения по фазам вероятность захвата равна
Где
Зо^лц., 51«в16(р/2а),д,=16(есЛ),ь(2^вт©.0) */©
— площадь колебательной области.
Рассчитывая Л, ^1 по гамильтониану Е~Н0 (см. (3), (5)), получаем
Таким образом, при прохождении через резонанс высокоэнергичных электронов вероятность захвата мала и основная часть электронов переходит из области обратного вращения (Ф*=©,—©<0) в область прямого (Ф = =©,—©>0) по траекториям типа траектории С на рис. 1.
При расчете Д/ используем результаты [6]. Для электрона, дважды прошедшего через резонанс (при движении в сторону большего поля и
Где величины зависят от значений фазы Ф в моменты перехода через
Сепаратрису, разделяющую области финитных и инфцнитных движений
|
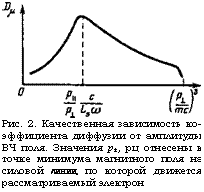
Рис. 2. Качественная зависимость коэффициента диффузии от амплитуды ВЧ поля. Значения Р±, рц отнесены к точке минимума магнитного поля на силовой линии, по которой движется рассматриваемый электрон |
 На рис. 1. В соответствии с [6—8] величины можно считать слу
На рис. 1. В соответствии с [6—8] величины можно считать слу
Чайными, независимыми, равномерно распределенными на отрезке (0, 1).
Тогда величину Д/ также можно считать случайной, имеющей нулевое среднее и дисперсию
„2 ( Р|1с* У ТС В,
* ' £.ш2 ' р± Е
' Р\ В0 с /
При этом коэффициент диффузии равен О»—(0Ь0Ц2.
Как известно (см., например, [ 11]), при достаточно низких амплитудах ВЧ поля, когда условия адиабатичности не выполняются,
В^(ср±Е/В0)2(лЬвт/рц(о)(Оь.
Таким образом, своего максимума коэффициент диффузии достигает на границе области адиабатичности, определяемой условиями (6), (7) (см. рис. 2). Отметим, что при (р\/р±) (с/Ьл(й)>{р±1тс)[83] коэффициент диффузии обращается в нуль, если Е/В0>(р\/р±) (с/Ь^ы).
Диффузию можно существенно усилить, если для нагрева использовать колебания с более сложным спектром, например, совокупность двух монохроматических колебаний с частотами, разделенными на Д©<©. Амплитуда результирующего ВЧ поля будет меняться из-за биений. Если электрон, двигаясь в сторону большего магнитного поля, проходит через резонансную область в период возрастания амплитуды ВЧ поля, то вероятность захвата повышается. Захваченный электрон увеличивает свою энергию в соответствии с условием авторезонанса е—тс2©е0/©. Уменьшение амплитуды ВЧ поля приводит к прекращению авторезонансного ускорения. За время пребывания в состоянии авторезонанса энергия электрона возрастает на Де=тс2(й)е>02—ю*")/со, где й)е°1 (ю^г) — значение циклотронной частоты в момент «входа» («выхода») в авторезонанс. Предполагается, что ©Д>©»°,1. Поскольку возможны также переходы с ю.*2<© *1,
То нагрев электронов имеет характер диффузии по е. Шаг диффузии максимален 3) при Д©~й)6.
Возможно, что описанный механизм нагрева проявился в экспериментах [4], где наблюдалось повышение эффективности нагрева при усложнении спектра ВЧ колебаний.
В заключение найдем максимальную энергию, которой может достичь электрон при ЭЦР нагреве. В гамильтониане (1) за нагрев ответственно последнее (малое) слагаемое ~ср±еА/г. В силу того что оно является резонансным — секулярным, с ним связаны изменения энергии Ье^>ср±еА/г. При их определении можно приближенно считать, что движение происходит ПО поверхности //(0,=е — Цй)=СОП81. Комбинируя это
Ц=[(Я(0))2-(тс2)2-(р„с)2],/‘/а).
Величина ц, а вместе с ней и энергия электрона е=Я(0,+ц(о будут максимальны, если резонансное условие выполняется в момент остановки при движении вдоль магнитного поля (рц=0):
Ц™={ 2ц. — [^=- - (1 + ^Р-)] +Цо2} ' , (9)
*• о) *- аз ' Тс ’ л *
Где ц0 — начальное значение магнитного момента, (дв,°тах — максимальное значение циклотронной частоты, достигаемое при движении по ловушке, до включения ВЧ поля.
В слаборелятивистском случае (9) удобно представить в виде Цтвхда
* (2ец.Тс2) 7,/о), соответственно е«««—тс2« (2 6 ц. гас2)’'ч Отметим, что то же самое выражение для ето* было получено в [12], где рассматривалось ДВИЖеНИе ЭЛеКТрОНОВ В СЛабоМ ВЧ ПОЛе. В ВЫражеНИЯХ ДЛЯ Цта*, втох вц, — начальная энергия продольного движения электронов в момент прохождения через резонансную точку. Если считать 8 ц* равной энергии электронов, рождающихся при ионизации (ец,~10 эВ), что соответствует условиям [2—4], то получим Гтах—тсг~ 1 кэВ.
3. Нагрев при движении поперек магнитного поля
При движении, описываемом гамильтонианом (1), электрон не может достичь энергий ~100 кэВ, наблюдавшихся в экспериментах [2—4]. Поэтому расширим рамки задачи, учтя новый фактор — движение поперек магнитного поля.
Предположим, что на некоторой силовой линии магнитного поля резонансное условие ь)=ь),(z) выполняется в точке минимума зависимости <ц,(z). Электрон с достаточно малой продольной компонентой импульса P\<^P±(ElBo)'lt{p±/mc)l, движущийся вблизи минимума магнитного поля, является авторезонансным. Практически во всех магнитных ловушках самопроизвольно возбуждаются НЧ колебания, вызывающие дрейф электронов поперек магнитного поля. Если скорость дрейфа направлена в сторону увеличения В0, а движение достаточно медленно (max(|<b,|Vl, |©«Г/,)<0)» то энергия авторезонансных электронов будет возрастать в соответствии С Условием Е = тс*й),°/й).
Дрейфовое движение в НЧ колебаниях, как правило, имеет случайный характер. В силу авторезонансного условия с пространственной диффузией должна быть связана диффузия по jr.
D^D(e/(oL±)
Где D — коэффициент пространственной диффузии, L± — характерный масштаб поперечной неоднородности магнитного поля.
Рассмотрим продольное движение авторезонансных электронов. Они локализованы в окрестности минимума магнитного поля, где d),°(z)« д(Oe,°min [14-(z/L0)a]. Предполагая, что ь),,0m*n=(je/тс*, из (3) получаем
Считая, что при дрейфе поперек магнитного поля наряду с поперечным сохраняется и продольный адиабатический инвариант /ц= $ P\dzy С помощью (10) находим Zmьx=(I\LJnp±)'h. Это выражение показывает, что по мере роста Р± размах осцилляций электрона вдоль магнитного поля уменьшается. Таким образом, авторезонансный нагрев должен приводить к образованию тонкого слоя высокоэнергичных электронов, локализованных вблизи поверхности (BoV)Bo=»0.
В экспериментах [2—4], где изучалось пространственное распределение высокоэнергичных электронов, поверхность циклотронного резонанса пересекалась с поверхностью (В0У)В0=0 по окружности. В этом случае высокоэнергичные электроны должны образовать кольцевой слой, что и наблюдалось в [2—4]. В силу существенной поперечной неоднородности магнитного поля в [2—4] дрейф авторезонансных электронов вполне позволял им достичь энергий —100 кэВ.
Авторы благодарны А. В. Звонкову за обсуждение работы.