ВЛИЯНИЕ РЕЛЯТИВИЗМА НА ОБРАЗОВАНИЕ ПЛЕЩУЩИХСЯ ЭЛЕКТРОНОВ ПРИ ЦИКЛОТРОННОМ НАГРЕВЕ
ЗВОНКОВ А. в., ТИМОФЕЕВ А. В.
1. В неоднородном магнитном поле область интенсивного взаимодействия между заряженными частицами и электромагнитными колебаниями ограничена малой окрестностью резонансной точки, в которой частота колебаний совпадает с циклотронной частотой. При прохождении частиц через эту область меняются их энергия и магнитный момент, что приводит к изменению траектории движения вдоль магнитного поля. Влияние резонансного взаимодействия на траектории электронов, удерживаемых в адиабатических ловушках, рассматривалось в [1—4]. В этих работах было показано, что увеличение энергии электрона при резонансном циклотронном взаимодействии имеет следствием приближение точки отражения электрона от области возрастающего магнитного поля к резонансной точке. Отсюда следует, чтр нагрев электронов должен сопровождаться появлением группы так называемых плещущихся частиц, движущихся по одной и той же траектории и отражающихся от магнитной пробки в точке циклотронного резонанса *. Плещущиеся электроны были зафиксированы в экспериментах [5, 6].
Появление плещущихся электронов может существенно изменить динамику плазмы при электронном циклотронном нагреве. Так, например* ожидается, что нагрев электронов в запирающихся частях амбиполярных ловушек приведет к росту амбиполярного потенциала. Однако плещущиеся электроны удерживаются магнитным полем, поэтому их появление должно сопровождаться падением потенциала и, следовательно, ухудшением удержания плазмы. Вместе с тем плещущиеся электроны, как и плещущиеся ионы [7], могут играть положительную роль, обеспечивая устойчивость аксиально-симметричных открытых ловушек по отношению к желобковым колебаниям.
В настоящей работе учтено влияние релятивизма на явление, рассмотренное в [1—4]. Показано, что если начальная энергия электронов <£ и величина амбиполярного потенциала <р0т* достаточно малы (<£ |еф0т|< <тс[72]), то циклотронный нагрев будет приводить к образованию группы плещущихся электронов. Определено максимальное значение энергии,, до которой могут быть нагреты электроны. Ограничение энергии при нагреве обусловлено релятивистским эффектом зависимости циклотронной частоты от энергии.
2. Движение электрона в адиабатической ловушке в присутствии электромагнитных колебаний описывается гамильтонианом
Я=-ефо(г)+с [(тс)Ч-(р + -^-А»(г) + -1-А1(г><) ) ] . (1)
Интересующий нас процесс резонансного взаимодействия между электронами и колебаниями разыгрывается в малой окрестности резонансной точки гс, где частота колебаний со кратна циклотронной частоте й)е(г)=^
=сеВ0(т)/(#+еф0(г)). В этой области удобно ввести локальную декартову систему координат, направив ось Z вдоль магнитного поля. Будем считать, что характерный масштаб изменения Фо(г), А0(г) велик по сравнению с ларморовским радиусом электронов. В этом приближения для фо(г), А0(г) можно использовать следующие выражения: ф0(г)=ф0(2), А0(г) =
*=(—#0(z)y; 0; 0). Примем, что электромагнитные колебания, распространяющиеся по плазме, имеют вид плоской волны: Ли(г, f) =^4lm - sin(kr— —.
Рассмотрим сначала движение электронов в отсутствии колебаний, положив в (1) А,=0. При помощи производящей функции (см., например, [8])
----- (у—JTctgO-arY^ +zPx (2)
Введем переменные, описывающие ларморовское вращение (0 — фаза лар - моровского вращения, I — поперечный адиабатический инвариант) и движение ведущего центра (Х=—сРг/еВ0, Y). В новых переменных невозмущенный гамильтониан Я0 принимает вид:
Яо=-ефо(Z) +с [ (тс)Ч-(2еВ0(z)I/с) +PS] Ч'=&. (3)
Теперь учтем влияние электромагнитных колебаний. Разложим (1) в ряд по Ai и оставим лишь линейное слагаемое. Используя новые переменные, легко выделить резонансную часть гамильтониана
+Jn+l(k±p.)At,+) (2efi.(z)//c)'<■+/„(*хР. МмР,], (4)
Где Jn — функция Бесселя; AT>^=(1/2) (Л^ sin Ф«*^^ cos Фпу) “ составляющие вектор-потенциала, вращающиеся в электронную (ионную) сторону; Ait\=An sin ФП1; Фп<=л0+А:||2—wf+an<; р.= (2СЦеВй)Чл.
Весьма существенно, что НХЫ) зависит от переменных 0 и T лишь через фазы Фп<. Учитывая это обстоятельство, находим
Dl ДН^П ЭЯ,"”
Dt д0 со Dt '
В дальнейшем нам понадобится также выражение для изменения величины которую мы будем называть энергией
Если 2Г—2С>р.%1»,#*, То электрон в процессе отражения от магнитной пробки дважды проходит через состояние резонанса с колебаниями (двигаясь туда и обратно). При 2Г—2с<рдва акта резонансного взаимодействия сливаются в один. Если время отсчитывать от момента остановки электрона (і7ц (г (0)) =0), то при вычислении полных изменений Гп <8 за одно отражение от пробки пределы интегрирования можно взять бесконечными:
|
(6) |
![]() Дгг=-яГ’ |Л + { л Ди["т,
Дгг=-яГ’ |Л + { л Ди["т,
Если электрическое поле колебаний обращается в нуль на достаточно большом расстоянии от точки поворота, то из (6), (7) следует
Где
— 00
Соотношение (8), по-видимому, справедливо при произвольной пространственной зависимости электрического поля колебаний, если его амплитуда достаточно велика. Действительно, известно (см., например, [4]), что при Е>Ес(Ес~В0(ср±/&)л/*(с/(йЬУ/*1 // — характерный масштаб изменения магнитного поля) движение электрона в адиабатической ловушке становится стохастическим. В данном случае стохастичность проявляется в хаотиза - ции фазы ларморовского вращения электрона за один акт резонансного циклотронного взаимодействия. Поскольку возмущенная часть гамильтониана Н 1(п) — гармоническая функция фазы 0, то хаотизация фазы ведет к эффективному уничтожению возмущения.
Знание величин & и ЪТ достаточно для описания движения электрона по ловушке. Однако в некоторых случаях состояние электрона удобнее - характеризовать величинами Р±г и рц1, отнесенными к минимуму магнитного поля Р±О2, ^ио2. Их изменения в результате резонансного циклотронного взаимодействия можно выразить через Д<2Г, используя постоянство - энергии и поперечного адиабатического инварианта на траектории электрона вне резонансной зоны. Простые вычисления дают
А_ , пш.(О) 2#Д«У
ДРх. —--------------------- :---- , (9)
Ш с
“V1—[73]
4. В стохастическом режиме движения электронов по ловушке их функция распределения по & и I будет расплываться диффузионным образом. Очевидно, что в среднем энергия электронов должна возрастать. Используя (9), (10) находим, что на плоскости Р±02 0Р\0г (рисунок) электроны движутся вдоль кривых, образующих однопараметрическое семейство
На плоскости Р±0[74] Ор^ частицы, останавливающиеся в точке 2С, располагаются на кривой, описываемой уравнением
#=-ефо(2.)+с[ (тс)г+р±О2 — 1 (12)
И Па, о Тс2 -*
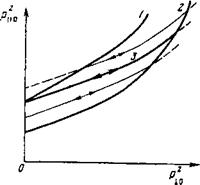 Приближенно (с точностью до размера резонансной зоны) можно считать, что наибольшая энергия, которой может достичь данный электрон, определяется пересечением кривых (11), (12). Электроны, лежащие на кривых (11), пересекающих конус потерь, будут выброшены из ловушки в
Приближенно (с точностью до размера резонансной зоны) можно считать, что наибольшая энергия, которой может достичь данный электрон, определяется пересечением кривых (11), (12). Электроны, лежащие на кривых (11), пересекающих конус потерь, будут выброшены из ловушки в
Движение электронов на плоскости Рхо2Орцо* при циклотронном нагреве. Под действием циклотронных колебаний электроны движутся по тонким кривым, которые описываются уравнением (8); 1 — граница конуса потерь; 2 — кривая, на которой располагаются электроны, останавливающиеся в точке циклотронного резонанса 2г=*2с; 3 — кривая, описываемая уравнением (11) при const— =*—<?фоТ+тсг
Процессе диффузии. Поэтому максимальная энергия достигается электронами, лежащими на плоскости Р±02 Ори1 на кривой 3 (const*—Еуйт+тсг, Фот - значение потенциала в пробке ловушки). При нерелятивистском потенциале |сф0т|<тс*, используя (И), (12), находим
Saux^Mc2 [1+ (2с| фот—фос|/тс*),/ш],
Где фас — потенциал в точке циклотронного резонанса Zc нерелятивистских электронов B0(Zc) ЖТтс/пе.
Ограничение энергии при циклотронном нагреве обусловлено релятивистской зависимостью циклотронной частоты от энергии электрона. Уменьшение циклотронной частоты с ростом энергии вызывает смещение резонансной точки Zc $ область большего магнитного поля. В результате на траектории электрона условие циклотронного резонанса перестает выполняться.
В области малых нерелятивистских энергий кривые (11), (12) вырождаются в параллельные прямые. Удаление электронов вдоль них от начала координат при циклотронном нагреве приводит к сжатию функции распределения по питч-углу x=arctg(/?xo/piio)- Этому процессу соответствует концентрация точек отражения Zr к точке циклотронного резонанса (см. (8)). Таким образом, нерелятивистские электроны стремятся стать плещущимися. Релятивизм ограничивает этот процесс. Однако поскольку приращение энергии при циклотронном нагреве Ал#* оказывается малым по сравнению с тс2(ДЛ^Г<^Гтах—mc2<mc2), то соответственно небольшим будет и разброс в значениях Zr для наиболее энергичных электронов (электронов, расположенных на плоскости Р±ог0рц* на кривой 2). Следовательно, при циклотронном нагреве наиболее энергичные электроны могут образовать группу плещущихся. Возникновение плещущихся частиц при циклотронном нагреве еще более характерно для ионов, так как релятивистские эффекты для них очень слабы.
Предположим, что точка циклотронного резонанса Хс находится в области возрастающего поля, где Fn(z)<0. Если электрон при своем движении вдоль магнитного поля заходит за точку ze(<M*r)><i>/n), то из (8) следует, что увеличение энергии электрона (Д2Г>0) ведет к уменьшению размаха продольных колебаний (Azr<0). Этот результат вполне естествен, поскольку при циклотронном резонансном взаимодействии меняется преимущественно поперечная энергия электрона (см., например, К]). Ее рост ведет к увеличению 1, а следовательно, и силы fg(z), направленной к
Центру ловушки. Так, например, в простейшем случае, логда электрическое поле колебании направлено поперек основного магнитного поля (£Г=&±), а электроны нерелятивистские (1=&±/СоР), из (5) получаем
TOC o "1-5" h z
|
417 |
![]() 1 / (д'(гг)
1 / (д'(гг)
6-г =----------- I---------------- 1 63 (П.1)
^|| (-г) V ©.(^ '
Поскольку на траектории электрона то (бгг/б<У)<0.
Однако в резонансном взаимодействии участвуют также электроны, не доходящие до резонансной точки (гс>гг), но останавливающиеся в пределах зоны резонансного циклотронного взаимодействия (~с—~r^p;/,L,/,). Увеличение энергии таких электронов, как следует из (8). ведет к удалению точки Гт от центра ловушки, что на первый взгляд противоречит (П.1). По-видимому, в этом случае полные изменения Л^г и Д# за одно отражение от пробки определяются различными участками траектории. Действительно, при 2Г<2С энергия электрона меняется наиболее быстро в малой окрестности точки отражения (:*гг), где он подходит наиболее близко к точке Гс. Предположим для определенности, что в этой области энергия электрона возрастает (О1^>0). Соответствующее изменение отрицательно и в силу условия
2«гг мало по величине (см. (П.1)). Когда электрон удаляется от точки Гг, электрическое поле колебании меняет знак. Вклад «второй» области в Д# отрицателен (б;# <0) и мал по величине, так как электрон теперь находится на большем расстоянии от точки циклотронного резонанса сс. Однако в силу увеличения множителя ((<й,(*г)/ /(|)г(г))—1) может оказаться, что 6ггг превзойдет по величине 1612Г|. В этом случае полные изменения Д&^б^+бг# п Дсг=б1Гг+б;сг будут одного знака (положительны). Именно это следует ИЗ (8) при Сг<2с.