К ТЕОРИИ АДИАБАТИЧНОСТИ ДВИЖЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ЛОВУШКАХ
ЗВОНКОВ А. В., ТИМОФЕЕВ А. В.
Заряженные частицы удерживаются в адиабатических ловушках лишь в той мере, в какой сохраняется поперечный адиабатический инвариант. Поэтому вопрос о его постоянстве имеет для адиабатических ловушек принципиальное значение. До сих пор при его аналитическом рассмотрении предполагалось, что профиль магнитного поля на оси ловушки параболический или слабо отличается от такового [1, 2]. В реальных системах зависимость магнитного поля от продольной координаты близка к параболической лишь у «дна» ловушки, где удерживаются частицы с малой продольной скоростью. Между тем известно, что неадиабатические эффекты особенно сильны для частиц с большой продольной скоростью, которые близко подходят к пробкам магнитной ловушки. Чтобы включить в рассмотрение такие частицы, в настоящей работе принимается, что магнитное поле на оси ловушки изменяется по закону косинуса (см. ниже). Такая зависимость довольно хорошо аппроксимирует реальные поля, характерные для многих открытых ловушек.
Согласно [3—5], к разрушению поперечного адиабатического инварианта приводит резонансное взаимодействие ларморовского вращения заряженной частицы с ее колебаниями между пробками ловушки. Процесс разрушения можно исследовать двумя способами: посредством прямого интегрирования уравнений движения и в рамках гамильтонова формализма. Первый способ, ведущий свое начало от работ [6, 7], применялся в [1, 2]. Мы использовали второй ввиду его методических преимуществ. Получен аналитический критерий разрушения адиабатического инварианта. С его помощью показано, что при P/L-*-0 область неадиабатично - сти на плоскости прилегает к конусу потерь. (Здесь р — ларморов-
Ский радиус заряженных частиц, L — характерный масштаб изменения магнитного поля). Причем как бы ни была мала величина р/£, всегда найдутся частицы, движущиеся неадиабатически. (Однако при р/£-*-0 их доля экспоненциально мала ~ехр(— Lip).)
В Приложении 1 показано, что аксиальная асимметрия магнитного поля, характерная для ловушек с min-5, практически не влияет на критерий адиабатичности. Влияние столкновений на движение заряженных частиц в адиабатических ловушках обсуждается в Приложении 2.
1. Примем, что магнитное поле на оси аксиально-симметричной ловушки изменяется по следующему закону:
B(z) = ±B'( (Я+i) - (Д-1) cos ( ™ ) ),
Где R — пробочное отношение, L — половина длины ловушки. Координата Z Отсчитывается вдоль оси системы.
Будем считать магнитное поле потенциальным. В приосевой области (r<L) магнитный потенциал имеет вид
Ф(г, г)=В0( V(Z)-±-T*V”(Z)) , V'(Z)=B(Z)/B* V(0)-1.
Я.7(т1)-Ф(г,*)-В.( 7(2)--^г*Г'(2)) ,
Где А в — азимутальная компонента векторного потенциала. Разрешая эти уравнения относительно гиг, получаем формулы, связывающие старые координаты с новыми
Г=§(V(л))_/* (1+^ (Г”(П) У (ч)-2 V*(л)) (Г (I,))-•) , (1)
*-П+-7-6*У"(ч)
4
Согласно определению, поверхности £=сопз1 представляют собой поверхности постоянного потока, а поверхности л=соп81 эквипотенциальны. Следовательно, силовые линии в новых координатах прямые, параллельные оси Оц:
В ={ 0;0;ЯУ( 1 -^.г(2У’"У'-2Уп) (П-*)} •
Нетрудно убедиться, что координаты 5, 9, Л ортогональны.
2. Движение заряженной частицы (для определенности рассматриваем ионы) в постоянном магнитном поле, как известно, описывается гамильтонианом
2пг х С
В новых координатах (£, 6, л) гамильтониан принимает вид
Я~^{р1гГ(1-£ЧЗГ''Г-4Г'г)/8У'а)+?-2(р.-та)(0£72)2Х
2т
ХГ'(1-1г(Р','Г'-27"*)/87'3)+р, г(1-1г(2Г,,Г-ЗГ, г)/47'5'}.
Теперь, следуя [8], введем координаты Ply gt, РГ, д2, которые в случае однородного магнитного поля были бы каноническими:
V * —(Pi+Pi+21/PiPi sin(gt+g2)), Та) Io
PiҐ=bptpz cosг (?,+g2),
Pe=p2—pl,
Tg0= (У2/?t cos Qi+V2p2 sin Qz) (V2sin gi+V2p2 cos g2)~
Где d)i0 — значение ионной циклотронной частоты при £=11=0.
Несколько упрощая, можно сказать, что переменные Ри Qi описывают ларморовское вращение, а переменные Рг> Q% — дрейфовое движение. Если рх/г-»-0, R/L-*0, то |1=ли;х2/2(1)<, gi переходит в фазу ларморовского вращения, Pt-*M(Df*L2Y Qt-+Q. Здесьр±в1;±/(1)< —ларморовский радиус ионов. При конечных, но малых величинах рJry R/L переменную Р{ можно представить в виде
/>,*|a(1+6*(V'*--F'"F)/8F'3).
Из этого выражения получаем
. ., 0>,'р.)* (Т'г-г"г) , , ч
Р Ц —2m----------------------------------------------------- V7*- 008 Я‘ 4 ’
Отношение второго слагаемого в правой части последнего выражения к
Следует, что вклад второго слагаемого в изменения Рх оказывается в (L/P±),T раз меньшим. Можно показать (см. также [1, 2]), что основные изменения Pi и 1* обусловлены центробежным дрейфом /ПУУцд/оїі,
Где Уцд=(У||7(0<) [ВV]B/B
В новых переменных Pi, Q{ гамильтониан приобретает вид
Я=Я0+Ь, |Л|«Я0,
Где Ho=(OiopiVу (л) +рпг12т,
Л=-2 — Ур^(<о1,р, Г+ —р, г)(2Г''Г-ЗГ"г)-^зт(?1+9г). mw<e х Т ' 4V
Здесь в Л оставлены лишь наиболее важные члены. Перейдем теперь к каноническим переменным для продольного движения, определив их формулами
Р, = (Д-1)) (Е- (1 -кг) К),
Л
?, = ^(arcsm(^sm^-), К),
Где /'Чф, К) — эллиптический интеграл первого рода, К, Е — полные эллиптические интегралы, а величина К определяется соотношением К= = ( (Я0—й)»оРі)/(0,0^1 (Д—1)) ‘/’. При этом преобразовании координата Qx переходит в Jil
Qi=Qi-(2M(XiioLi(R-I)Lpiy,IZ(2Kq3Ln)Y
Где Z — дзета-функция Якоби [9].
Как известно, разрушение поперечного адиабатического инварианта вызывается резонансным взаимодействием ларморовского вращения с продольными колебаниями частицы [ 3—5]. Чтобы выделить резонансные члены в гамильтониане, нужно H разложить в ряд Фурье по Q3. Для нахождения I-того члена ряда требуется вычислить интеграл
,_J «Г-Г-
Где
Ч?=g1+^3+g2- (2ML2Toi0 (R-L) Lpl)4TZ(2KqJn).
Интегрирование удобно проводить, смещая контур интегрирования в комплексную плоскость так, чтобы он проходил около полюса подынтегрального выражения, где F'=0. Положение полюса определяется уравнением
Dn2(2Kq3/N)=R/(R-I)Y
Где dn — эллиптическая функция. При выполнении резонансного условия ДН0 дНа
Qt—Lq3S=------- 1---- = 0 оказывается, что полюс является и точкой ста
Дії Др3
Ционарной фазы, т. е. в этой точке —;— = 0. В этом случае асимптотиче-
Dq3
Ское значение интеграла J при £^Рх (Рх*®^/®*) выражается через Г-функцию.
Проводя все вычисления, получаем
«•
Я—Н,+ Xjfta, cos (g,+g»-2ng,), (2)
•■»в
Где Нож(діоРі(1+кг(R—1)), H,N= (Злг/6К)(йі0Рх(2РгІтЬг(йі0)Чі(R-L)4T exp {-(2MLi(X>Io(R-I)ІзїрУ'Х 322
Ф0=*агс5т((Я—1)/Л) а штрих указывает на то, что модуль эллиптических интегралов равен (1—Кг)ч
Условие резонанса можно привести к следующему виду:
(1/я2) (2ТЬгацо(Н—)1Р1)ъ(КН/(И—1)—Е) =п. (3)
3. Под влиянием возмущения А частица совершает колебания на плоскости РЛр*. Особенно велики эти колебания вблизи резонансных кривых, определяемых (3). Согласно [3—5], движение становится стохастическим, когда резонансы перекрываются, т. е. амплитуда колебаний частиц, расположенных вблизи резонансных кривых, перекрывает расстояние между соседними резонансными кривыми.
Чтобы найти ширину резонанса, предположим, что изменения величин Ри рз достаточно малы (Ьр^рх, бРз^Рг-Х- Переходя к переменным Р, описывающим отклонения от резонансных значений,
/>1—РГ*+Р, р,=р,(л>—2пР, ^=д,-2пд3
И разлагая Н0 в ряд по Ру получаем гамильтониан в виде
1
Н =—Рг-Ь2п сое (?,
2М
Где
ДгН дгН дгН
М-'« —7 -4П-—+ 4л2 —— (й)<о/2/>1(Д-1)Кг(—кГ))X Ор * Др1 др3 др3г
Х{(-кг(-к2) (Н-1)г+(+к*(Н-1))г)Е/К-(-(Н-)гкг) (1 - А1)}.
Теперь можно определить ширину резонанса [ 5 ]
6Р=А(к2пМ)', (4)
Условие перекрытия имеет вид
(6Р'-1Ч)^Д Р, (5)
Где 6Р'=(1, — 2п)6Р, единичная нормаль к резонансной кривой на
Плоскости Р10рзУ а Др — расстояние между соседними резонансными кривыми, которое находится из (3).
Условие (5) можно также представить в виде 2й)нл>й)3, где ювл= = (И/М)7* — характерная частота нелинейных осцилляций резонансных
ДН. я* / о,0(я-1)/?1 V'*
Частиц, (оЗ = —г—д, „I ------------- I — частота продольных коле-
Др з 2 ЬКХ 2т '
Баний.
Условие перекрытия приобретает простой вид для частиц, движущихся у дна ловушки (&-*■0), а также для частиц, отражающихся у пробок (&-*-1). Чтобы получить случай параболического магнитного поля, следует перейти к пределу при &2Д^1. Тогда получаем условие пере
Крытия резонансов
4 рх.2 ' Я2 ' I 2р±0 Я 1 2 Ч-Л /
Где £0=2£/лУЛ— 1, Ь—и±о/и. Это условие вполне согласуется с результатом работы [2].
В другом предельном случае при 1—&2<1 условие перекрытия выглядит следующим образом:
— ~~ехр{------ —( -1+——Arcsin—)} >1—А2. (7)
Я* (д-i)’1 рх»1 1 ярх. гя-1 Тп
Из (7) следует, что вблизи конуса потерь (&-»-1) движение неадиабатично при любых значениях ЫР. Причина этого ясна. Для частиц, достаточно близко подходящих к пробкам ловушки, период движения неограниченно
|
|
|
|
|
|
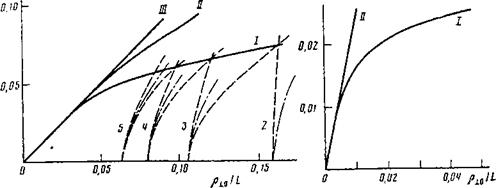
2 — 1, граница конуса |
![]() Рис. 2. Граница области адиабатичности при й=7 и ^ ~£~)
Рис. 2. Граница области адиабатичности при й=7 и ^ ~£~)
Потерь - II
Возрастает. Поэтому даже малые изменения магнитного момента имеют следствием значительные изменения фазы ларморовского вращения, что, согласно [3—5], и ведет к неадиабатичности.
Условие перекрытия резонансов исследовалось также численно. На рис. 1 штрихпунктиром изображены резонансные кривые на плоскости (Рхо/£, РноД») для ловушки с пробочным отношением Д=2. В окрестности каждого резонанса частицы колеблются в пределах области, ограниченной пунктирными линиями, положение которых находилось в соответствии с формулой (4). Пересечение пунктирных линий, принадлежащих соседним резонансам, определяет границу области стохастичности (кривые I, И). Следует отметить, что в окрестности первых резонансов гс**1, 2, 3,... амплитуды колебаний брхо, брцо, вычисленные формально по (4), оказываются сравнимыми с самими величинами рхв, рно. Поэтому использование формулы (4), полученной в предположении брхо^Рхо, бРно^Рио, становится, строго говоря, неправомерным и, следовательно, граница области стохастичности приобретает условный характер.
На рис. 2 приведена граница области стохастичности для ловушки с большим пробочным отношением Я—1.
4. Критерий адиабатичности движения заряженных частиц может быть также получен непосредственным анализом уравнений движения [1, 2]. Этот метод основан на вычислении приращения Дц за одно прохождение по ловушке (см. также [6, 7]). При интерпретации результатов расчета иногда используется представление о «скачках» — Дц, которые привязываются к моменту прохождения частицы через минимум магнитного поля.
В гамильтоновом формализме операцией, эквивалентной подсчету Дц. является выделение из возмущенной части гамильтониана резонансной фурье-гармоники. Именно эта операция определяет показатель экспоненты в условии адиабатичности (см. (5) —(7)).
Из (2) следует, что показатель экспоненты — довольно сложная функция пробочного отношения И и параметра &, характеризующего амплитуду колебаний частицы вдоль магнитного поля. Уже отсюда можно сделать
ВЫВОД, ЧТО Изменение Ц, Вообще говори, Иирс^«»-------------- -
Частицы, а не только той ее частью, которая лежит в окрестности минимума магнитного поля. Соответственно и часто используемое приближение параболического магнитного поля, которое безусловно справедливо в окрестности минимума, можно использовать при подсчетах Дц лишь для частиц, удерживаемых на «дне» ловушки.
Что касается представления о скачках ц, то оно, на наш взгляд, более адекватно при описании резонансного взаимодействия заряженных частиц, движущихся в неоднородном магнитном поле, с электромагнитными циклотронными колебаниями (см., например, [10]). В этом случае магнитный момент испытывает резкое изменение (скачок) при прохождении через резонансную зону, где частота электромагнитных колебаний близка к локальной циклотронной частоте. Если резонансное условие ©=(0,(2) нигде на траектории частицы не выполняется, например ш<тш <0.(2), то резонансная точка «выходит» в комплексную плоскость. Однако при со. о— область изменения ц остается привязанной к «дну» ловушки. В нашем случае резонансная составляющая возмущения гамильтониана играет ту же роль, что и внешнее электрическое поле. (Частоту эквивалентного электрического поля следует считать равной нулю.) Нетрудно сообразить, что область минимума магнитного поля будет определять скачок Ац лишь при Д>1, когда в основной части ловушки ©,>1шп ©<(2).
В заключение заметим, что в настоящей работе, как и в [1, 2], рассматривалась лишь приосевая (параксиальная) часть ловушки. (В [1], как следует из анализа, проведенного в [2], приближение па - раксиальности использовалось неявно.) Условие параксиальности оказывается довольно жестким. Действительно, из (1) следует, что параметр параксиальности равен (г/Ь)2(Во/В(г))3. Приращение Дц за одно прохождение по ловушке или эквивалентная ей величина — амплитуда резонансной фурье-гармоники — определяются малой окрестностью точки комплексного переменного 2, в которой магнитное поле обращается в нуль. Это обстоятельство приводит к эффективному возрастанию последующих членов разложения по (г/!»)2. В результате условие параксиальности принима-
Ет вид r2<Lv, p^*.
ПРИЛОЖЕНИЕ 1
|
Учет аксиальной неоднородности магнитного поля. Проанализируем движение ионов в приосевой части адиабатической ловушки с квадрупольным тш-£. В этом случае магнитное поле описывается скалярным потенциалом вида
Где величину G, характеризующую квадрупольную составляющую магнитного поля, полагаем постоянной. Движение заряженных частиц удобно исследовать в «естественных» координатах, определяемых таким образом, чтобы координатные поверхности совпадали с магнитными. Потребуем также, чтобы в пределе однородного магнитного поля (V"жg=0) координатные поверхности совпадали с координатными поверхностями цилиндрической системы координат. Для таких координат получаем следующие выражения [11]: |
А=(г2/2) V' (z) (sin2 0 exp (C(Z)) + cos2 0 ехр(-с(г))). P=arctg(exp (c(z)) tg0.
X
Где с (2)— 2G J DzfV'(Z). Третью координату tj удобно определить равенством
0
B*V(Т|) = Ф(г) [6].
В новых переменных гамильтониан иона принимает вид
Я*(1/2т){(Уо)2ра2+2(Уо. Ур)ра(рр-(вВ0/с)о) + (УР)2(рр-(<?Во/с)о)2+(Ул),Рл2},
Где (Va)2^2ar(chc-cos2&shc), Va-Vp*7' sin 20 sh с, (Vfl)2* (V72a) (ch c+ +cos2(Jshc), (Vi))t=B1/Bo2Vtz. Последнее равенство следует из соотношения В= — УФ. используя которое, также находим
В»В,<*"+ <a/4V'*)[ (4?*+3V"*-2K"'Г) (ch с+соз 2? sh с) -8GV" (sh c+cos 2p ch c) ]}. Чтобы отделить ларморовское вращение от дрейфового движения, произведем
То же каноническое преобразование, что и в разд. 2 настоящей работы, заменив при этом £2/2—а, Рг+12ара, 0-*{J, ре-*рр. В новых переменных имеем
1
Tf=<Di0V'(ch с—cos 2gishc)pi + — (BIB0V')2Pn2.
2 Т
Магнитный момент ц и фаза ларморовского вращения Q вводятся посредством еле* дующего канонического преобразования:
H=pi(ch с-cos 2qi sh с),
Q=arctg (ectGqt),
H=H0+h, Я0=й)<0цУ'(Л) + (1/2т)р|,2,
Л=(рл72/п)(р2ц)’МГ)-3-[(^-»-зГ'2_2Г"Г)(сЬ (c/2) sin «?+<?2) +
+sh (c/2) sin (<?-<?j))-8gV'(ch (c/2) sin (<?-?2)+sh (c/2) sin (<?+«2))]-
Последнее преобразование изменяет также продольный импульс. При этой в гамиль - тониане появляются малые слагаемые ~(Pr^.FmL)F(Q), где функции F(Q) содержат гармоники ~cos KQ, sin KQ с K^2. Для анализа сохранения адиабатического инварианта такие слагаемые несущественны, и мы их опустили.
Переход к каноническим переменным для продольного движения и выделение резонансных членов в возмущении H производится так же, как и в аксиально-симметричном случае. В результате получим
Оо
Л—(1/2) ^JhZnexv(I(Q-2Nq3 + Q2))+К. с. (П1.1)
П—О
Hm^hzn* (ReD+exp (-2ig2)lmD),
Где Hzn* - соответствующее выражение для симметричного поля (см. (2)), а
0=(1+(4|/3)х-х*/3)Г“1 (2-x/4i) [Я2(1+Л*(Я—1))/44 (Я—1) (Я+£2(Я—1)) ]*/4<, х=2GL/NiR, A={L/N) • (2/пйх0(Д-1)/ц)Ч
В аксиально-симметричном случае х=0, D=1 и А271=Л2«*.
При наличии асимметрии в гамильтониане H наряду со слагаемыми ~ехр {I(Q—2Nq3+Q2)) появляются слагаемые ~ехр (I{Q—2Nq3—Qz)). Соответственно получаем две системы резонансов Q-2Nq3±Qz=0, где Q3~ (p/L)d>i, Q2~ (p/L)2©«.
На плоскости ji, P3 расстояние между резонансными кривыми с разными номерами П Намного превышает расщепление, вызванное аксиальной асимметрией. Поэтому наличие асимметрии практически не влияет на условие «перекрытия резонансов». Оно выполняется, если I Hzn | превышает некоторое критическое значение. В Hzn можно выделить экспоненциальную часть с показателем ~L/р и предэкспоненту. Последняя весьма слабо (логарифмически) влияет на критическое значение р. Из (П1.1) следует, что параметр х, характеризующий аксиальную асимметрию системы, не входит в показатель экспоненты. Магнитная яма обеспечивается уже при х~1, поэтому для реальных систем с min-fi порядок предэкспоненты останется таким же, как в аксиально-симметричном случае. Эти соображения показывают, что аксиальная асимметрия вблизи оси ловушки должна слабо влиять на критические значения р. определенные выше. Действительно, в приосевой области ловушки с min-fi отличаются от простых пробочных ловушек лишь зависимостью В от поперечных координат, что не сказывается на анализе адиабатичности.
ПРИЛОЖЕНИЕ 2
Учет столкновений. Выше была определена граница области неадиабатичности. в которой движение ионов в фазовом пространстве хаотическое - диффузионное, даже без случайных воздействий. В области адиабатичности резонансные частицы совершают регулярные осцилляции по фазовой плоскости. При этом существует опасность, что слабые случайные воздействия (кулоновские соударения) приведут к возникновению усиленной диффузии, аналогичной неоклассической.
Эту возможность проанализируем с помощью следующей системы уравнений, описывающей движение ионов вблизи л-го резонанса:
X-anSin QN,
Фп=Рп (X~X") (П2.1)
X»t=fc(0-
Здесь учтено, что возмущение H меняет питч-угол иона но не его энергию; впж *=**»,/ (2р |А (Я—1)v*), P„“2/>ifc(fl-l)v, Av, Qn’AKQi—2Nq3+Q2, где величина М определена в разд. 3 настоящей работы, fc (T) — случайная функция, 6-коррелированная во времени, посредством которой учитывается влияние кулоновских соударений '£(*1)£(*2)>вогб(Г1—12). Величина а* по порядку равна частоте кулоновских соуда
рений. Случайные воздействия помимо изменения питч-угла приводят также к непосредственному изменению резонансной фазы @п, однако это влияние оказывается слабым, и здесь не учтено.
Из (П2.1) находим следующее выражение для коэффициента диффузии по углу X в окрестности л-го резонанса:
|
О |
Где Ксо» Q„ (х) - корреляционная функция
А’со. Q„ (X) — (1/2) (cos (Мх-Х»)т+<?п.
Qn. $t(x) - приращение фазы, обусловленное случайными воздействиями. В силу центральной предельной теоремы величина Qn,»T(т) имеет нормальное распределение, и следовательно, справедливо соотношение
А’со» <?п(т) = (1/2) cos фп(Х“Х»)т) ехР Dis(T)b
Где Dis (т) = (1/3)ря*о*т3 - дисперсия фазы Qn.
Для коэффициента диффузии Dn можно получить аналитические выражения в двух предельных случаях:
|
(П2.2) (П2.3) |
![]() Dn * Г( 1/3)Gtr»2/(6Я„a)z/a, |x-Xn|ЯN о*
Dn * Г( 1/3)Gtr»2/(6Я„a)z/a, |x-Xn|ЯN о*
Dn * 2аN2a2/(Яn*(x-X")4), ІХ”ЗС»ІР» > <**•
Коэффициент диффузии определяемый выражениями (П2.2), (П2.3), является резко меняющейся функцией питч-угла х - Для нахождения усредненного (эффективного) коэффициента диффузии следует использовать формулу [10]
|
Xn+AX/t
Хд-Дх/t |
|
Откуда получаем |
![]()
|
(П2.4) |
![]() 0Ef~2Ean*o7(Яn2(Ax)4).
0Ef~2Ean*o7(Яn2(Ax)4).
Нас интересует режим, в котором соседние резонансы ве «перекрываются» ((МАх)2^®«* ?». - расстояние между резонансами). В этом режиме, как следует из (П2.4), добавочная диффузия всегда меньше чисто столкновительной О9п^ог~у.
Отметим, что выражение (П2.2) справедливо лишь при о4/,Рп1/,3*<Хп когда столкновения препятствуют «захвату» частиц при значениях х**Хп - Однако поскольку соответствующая область имеет малый размер, а коэффициент диффузии здесь резко возрастает, она не влияет на величину Лвгг, в этой области оказывается несущественным, ср. с [101.
Осцилляции адиабатического инварианта резонансных частиц могут оказаться существенными в том случае, когда динамика ионной функции распределения определяется столкновениями с электронами. При уменьшении И из-за трения ион пересекает резонансные кривые на рис. 1. В окрестности п-го резонанса ион испытывает скачкообразное приращение питч-угла х - Изменения х зависят от фазы Qn, значения которой в окрестности соседних резонансов нескоррелированы. Поэтому изменения х будут иметь диффузионный характер. Рассматриваемое явление описывается системой уравнений (ср. с. (П2.1))
|
(П2.5) |
![]() X=on sin QN, Qn=P/M,
X=on sin QN, Qn=P/M,
|
|
Здесь последнее уравнение учитывает замедление ионов на электронах с характерным временем V.“*. В нем не учтено действие секулярного возмущения, а в уравнении для - действие трения. Это справедливо при р/L» (ve/(i>i)Vi и »(г/L) exp (-CL/Р), С - константа порядка единицы.
Из (П2.5) находим скачок Ах при прохождении резонанса
Поскольку расстояние между резонансами &Pi**Pip/L ион проходит за время AЈ»p/(Lv,), то коэффициент диффузии по питч-углу равен
D*>4AnLM/(Npip)~ (to^/pL) exp (-2СХ/р)«шіп {VetL/(IО, р); w, (p/L)3}.
Если (R/L) exp {—CL/P), то правую часть последнего уравнения в (П2.5) не
Обходимо дополнить резонансным слагаемым Л2п cos Qn- В этом случае скачок Ах ра -
D»an[67]LeM/(hinp)~ (ver/p) exp (-CL/p) <vep/L.
Рассматриваемый механизм рассеяния по питч-углу может оказаться более существенным, чем классический, обусловленный ион-ионными соударениями при достаточно больших значениях ve и р.
В заключение заметим, что в аксиально-асимметричных системах кулоновские столкновения могут приводить к радиальной диффузии резонансных частиц. Однако рассмотрение показывает, что в простых адиабатических ловушках этот механизм диффузии, родственный неоклассическому, будет незаметен на фоне более быстрого ухода через пробки.