МОДУЛИРОВАННЫЕ ПУЧКИ В ЦИКЛОТРОННЫХ КОЛЕБАНИЯХ НА УСТАНОВКЕ АС
В. Г. ЖУКОВСКИЙ, А. В. ТИМОФЕЕВ
Первоначально считалось (см., например, [4]), что при циклотронном резонансе в неоднородном магнитном поле энергия колебаний тратится на работу против сил трения, вызванных кулоновскими соударениями. Причем, как бы ни была разрежена плазма, кулоновские соударения должны обязательно проявиться в окрестности резонансной точки.
Дальнейшее развитие теории, однако, показало, что если выполняется
|
(г) |
![]()
|
Условие |
![]() А оно выполняется практически во всех системах,
А оно выполняется практически во всех системах,
|
Юогм |
![]()
 Предназначенных для магнитного удержания плазмы, то обмен энергией между коллективной степенью свободы (самосогласованные циклотронные колебания) и индивидуальными (вращение заряженных частиц по ларморов - А(71Х°) ским окружностям) происходит по-иному. А именно, в окрестности резонансной точки возбуждаются модулированные пучки, образованные сгустками наряда, упорядоченно расположенными на циклотронных окружностях. Такие пучки свободно распространяются вдоль магнитного поля и в определенном смысле аналогичны хорошо известным волнам Ван-Кампена [*]. Эксперименты, проведенные на установке АС, дают, по-видимому, первое подтверждение теоретических воззрений.
Предназначенных для магнитного удержания плазмы, то обмен энергией между коллективной степенью свободы (самосогласованные циклотронные колебания) и индивидуальными (вращение заряженных частиц по ларморов - А(71Х°) ским окружностям) происходит по-иному. А именно, в окрестности резонансной точки возбуждаются модулированные пучки, образованные сгустками наряда, упорядоченно расположенными на циклотронных окружностях. Такие пучки свободно распространяются вдоль магнитного поля и в определенном смысле аналогичны хорошо известным волнам Ван-Кампена [*]. Эксперименты, проведенные на установке АС, дают, по-видимому, первое подтверждение теоретических воззрений.
Нами использованы обозначения:
|
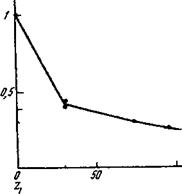
Корреляция циклотронных колебаний вдоль установки АС. Опорная точка расположена у самого края |
![]() V* — частота соударений частиц сорта /®*в, і, со* — циклотронная частота, г* — ларморовский радиус, Ь — характерный масштаб изменения магнитного поля, показатель степени а меняется от */з при резонансе в экстремуме магнитного поля до 7г при резонансе вдали от него.
V* — частота соударений частиц сорта /®*в, і, со* — циклотронная частота, г* — ларморовский радиус, Ь — характерный масштаб изменения магнитного поля, показатель степени а меняется от */з при резонансе в экстремуме магнитного поля до 7г при резонансе вдали от него.
1. Установка АС представляет собой открытую магнитную ловушку с простым пробочным полем. В ней, так же как и во многих других подобных системах, самопроизвольно возбуждались ионные циклотронные колебания. Исследования (см. [*]) показали, что в установке АС мы имеем дело с несколькими типами неустойчивых циклотронных колебаний, которые различаются по своим характеристикам и условиям возбуждения. Одна из неустойчивостей, которая в работе [1 ] была названа первой, раскачивается на ветке замагниченных электронных ленгмюровских колебаний за счет анизотропии в распределении ионов по скоростям. Детальное обсуждение этой неустойчивости будет дано в другой работе, здесь же мы
проанализируем результаты исследования пространственной структуры колебаний. Измерения показали, что в результате неустойчивости возбуждаются хаотические электрические поля, пространственная корреляция которых ослабевает довольно причудливым образом (см. рисунок). На графике выделяются два масштаба [40] корреляции: больший ах«200 см и меньший а2<0,1 а1г Наличие двух корреляционных масштабов свидетельствует о присутствии двух волновых процессов. Они имеют одну и ту же частоту, но различаются по своим пространственным свойствам. Очевидно, что длина волны не может превышать характерного корреляционного масштаба. Поэтому мы вынуждены считать, что плохо скоррелированный в пространстве процесс обязан коротковолновым колебаниям с длиной волны Х*<15-т-20 см.
В то же время непосредственные измерения показали, что в плазме имеются и длинноволновые колебания с А-^130 см, которые естественно сопоставить с большим масштабом корреляции. Заметим, что в силу низкой разрешающей способности аппаратуры (зонды были разнесены на расстояние ^30 см) колебания с ^*<30 см не могли быть обнаружены в измерениях. По этой же причине значение аг=20 см — верхняя граница для меньшего корреляционного масштаба.
Таким образом мы приходим к необычной ситуации: одной и той же частоте соответствуют два типа колебаний с различной длиной волны и различным образом скоррелированные в пространстве. Трудность усугубляется еще' и тем, что среди обширного набора циклотронных неустойчивостей (например, [[41]]) не оказалось такой, которая в условиях установки АС имела бы длину волны, равную или меньшую 20 см.
2. Чтобы разрешить эти затруднения, мы обратились к теории циклотронных колебаний в неоднородном магнитном поле, которая к настоящему времени развита достаточно подробно (см., например, обзорную работу [а]). Неоднородность магнитного поля должна сильно влиять на интересующие нас колебания, поскольку как их инкремент, так и ширина спектра меньше изменения циклотронной частоты в пределах области, занятой плазмой. В соответствии с [*] в неоднородном магнитном поле обмен энергией между частицами плазмы и циклотронными колебаниями обязательно сопровождается возбуждением модулированных пучков. Колебания, вызываемые модулированными пучками, аналогичны известным волнам Ван-Кампена. Различие лишь в том, что из-за наличия магнитного поля сгустки заряда, образующие пучок, движутся не по прямым, а по спиралям. Частота колебаний, связанных с пучками (мы их будем называть вторичными), равна частоте основной волны. Они представляют собой волны, убегающие от резонансной точки.
Если распределение ионов по скоростям в направлении вдоль магнитного поля имеет вид б - функции, то пространственная зависимость вторичных колебаний дается выражением
Ф(г) ~ ехр|{| А|,и((2)—п<о,(*)|. (1)
Здесь ось ОХ направлена вдоль магнитного поля, 2, — резонансная точка, о)*=Л(1)<(2,), ©<(г) —циклотронная частота ионов, кц — продольная компонента волнового вектора первичных колебании, л — целое число.
3. Рассмотрим теперь, как влияют модулированные пучки на корреляционные свойства колебаний. Фаза модулированного пучка однозначно связана с фазой циклотронных (первичных) колебаний в момент образования пучка, т. е. прохождения потока ионов через точку циклотронного резонанса. Если фаза первичных колебаний скоррелирована на интервалах времени порядка Af, то за это время вторичная волна уйдет от резонансной точки на расстояние Az=i;,|Af. Именно этой величине и будет равен пространственный интервал корреляции вторичных колебаний аг. Характерное время корреляции рассматриваемых колебаний «10“в сек (ширина спектра Асо«10в рад/сек) [*]. Оно примерно на порядок величины меньше
Периода колебаний иона по ловушке ------------- »10~ьсек, £«200 см, и±9«
V±o
«1,3-10® см/сек. Таким образом, в условиях установки АС должен действительно наблюдаться эффект пространственной расфазировки модулированных пучков и самосогласованных колебаний.
Прп измерениях опорная точка (начало координат на рисунке) была расположена у самого края плазмы. В этой области частица движется по
Закону z« .^r10^10 t2, здесь Уц0«5-Ю7 см! сек — продольная скорость иона
В минимуме магнитного поля. За характерное время изменения фазы колебаний ион сместится примерно на 20 см, что хорошо согласуется с экспериментальной величиной малого масштаба корреляции а2« 15—20 см.
Больший корреляционный масштаб естественно связать с распространением первичной волны (самосогласованных колебаний) a, i~v*kt, здесь
Р* = _ групповая (фазовая) скорость замагниченных электронных
Ленгмюровских колебаний, к раскачке которых приводит анизотропная циклотронная неустойчивость. Вычисленное таким образом значение at«3,3- •10* см примерно в два раза превышает найденное в эксперименте. Расхождение, по-видимому, связано с резким-замедлением волны у границы плазмы (ее длина примерно равна 200 см).
Институт атомной энергии