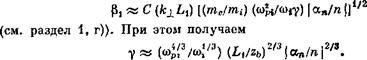НЕРАВНОВЕСНАЯ ПЛАЗМА
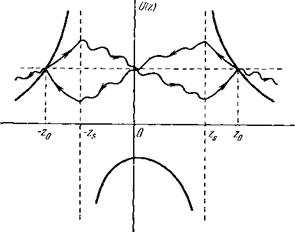
1. Резонансное циклотронное взаимодействие в неравновесной плазме, а) Однородное магнитное поле. В реальных условиях распределение частиц плазмы по скоростям часто отличается от равновесного, максвелловского. Неравновесность может быть связана с наличием пучков, анизотропией функции распределения (неравенство средних энергий в направлении поперек и вдоль магнитного поля), отсутствием в распределении по поперечным скоростям частиц с малыми скоростями и т. д. Как уже отмечалось, распределения, обедненные частицами с малыми поперечными скоростями, характерны для магнитных ловушек. Такие распределения, называемые конусными, и будут нас интересовать. Для того чтобы выделить эффекты, связанные с наличием конуса потерь, необходимо рассмотреть колебания, обладающие некоторой пространственной структурой в направлении поперек магнитного поля. В простейшем случае — это плоская волна, с волновым вектором, перпендикулярным к магнитному полю: Е = Е (sin (ш£ — кх); 0; 0). Довольно громоздкие расчеты приводят к следующему выражению для скорости изменения энергии заряженной частицы (иона) под действием поля волны [30]):
DWi/dt = W2) (4-i (s)—4+1 (*)) {еЩ2/гт) t; (2.1)
Здесь s = krit гг = у^/о); —ларморовский радиус ионов, рассматривается резонанс на п-й циклотронной гармонике ш та ио);.
Выражение (2.1) отличается от (1.1) множителем
Ап (s) = (п/2) (4-1 (в) -4+1 (в)) - (n2/s) (4 (s))'s.
При s п
Ап (s) « US/2P (п + 1)] (sl2)2‘"-1>,
А при s п имеет колебательную структуру 2в, Ап (s) л* « (—1)п (2n2!ns2) cos 2s. Если Ап (s) < 0, то кинетическая энергия ионов под действием поля волны будет уменьшаться и, следовательно, в силу сохранения энергии волна,— нарастать. В этом случае циклотронное взаимодействие приводит к излучению, а не к поглощению колебаний. Поясним этот результат. Разложим плоскую волну по цилиндрическим
Оо
В соответствии с известной формулой e±ihx = Jn (s) е±,п9; здесь
71 = — ОО
Х = гг sin 0,0 — азимутальный угол, начало координат выбрано в центре
Оо
Ларморовской окружности. В силу равенства 29 У! = 1, всс п-й
71=—.оо
Цилиндрической гармоники в разложении равен J*. В системе координат, связанной с частицей, частоты отдельных цилиндрических гармоник равны
Ауп = (о — пв, где 0 = соf. Очевидно, что слагаемое и0 играет ту же роль, что и допплеровский сдвиг АцУц для волны, периодической вдоль магнитного поля. По аналогии с этим случаем можно говорить о нормальном
И аномальном допплер-эффектах <оп = а> — пв = ч-(ог. При нормальном допплер-эффекте энергия поглощается заряженной частицей и при аномальном излучается. Поскольку 0 = для колебаний с со — пш-, будет поглощаться (п — 1)-я цилиндрическая гармоника и излучаться (п + 1)-я. Эффект излучения преобладает, если вес (п + 1)-й гармоники в разложении плоской волны окажется большим.
Для совокупности частиц с некоторым распределением по поперечным скоростям /о t (wjJ результирующий эффект определяется средним значением Ап (s):
00
Ап — 2л j dv±v±f0 ' (vj Ап (s).
О
Величина ап может стать отрицательной, если распределение обеднено в области малых скоростей vj_ < n<щjk^, так как при этом из интеграла по dvM вырезается область малых значений s, где Ап (s) > 0.
Б) Магнитное поле, монотонно меняющееся в пространстве. В связи с проблемой устойчивости плазмы в адиабатических ловушках интенсивно изучались замагниченные электронные лэнгмюровские колебания в области частот w « n(щ{. Адиабатическое волновое уравнение, описывающее эти колебания, имеет вид (см., например, 13> 14• 30)
5+*1(у2[1-Н=Л&$]»-0; (2.2)
Здесь ф (z) — возмущенный потенциал, ф (г, t) — ф (z) е lь)i+lklr_L) частота колебаний считается близкой к пса,, поэтому из суммы по п, которая, вообще говоря, должна присутствовать в (2.2), оставлено п-е резонансное слагаемое, и зависимость от координаты z учитывается лишь в резонансном знаменателе. Это приближение справедливо при (шР1/ш,) | аП1п | */2 1,
Т. е. при достаточно низкой плотности плазмы или при достаточно больших значениях (Для конусных распределений ап « —2~3/2л~1^п~2(к1г^)~3у
(s>n
Здесь rt — средний ларморовский радиус ионов.)
После ряда переобозначений (2.2) приводится к (1.9), соответственно-
(2.1) — к (1.1). Поэтому резонансное взаимодействие в неравновесной плазме можно описывать выражениями, полученными в разделе 1, г). При ап < 0 удобно ввести
Pi = — p = 2i j &|| dz,
20
Где Агц находим из (2.2):
К„ = к±^L[i------------ ]!'2.
11 (Ope L nwt (w— nCщ, (z)) J
В магнитном поле, меняющемся по линейному закону,
Pi = —л (а„/п) (mjm,)V2 (k±L) ы)pi/ы),.
По аналогии с (1.17), (1.20) имеем (см. 14)
Ti = еР*/2, (2.3)
G, = | Д, |г = (eh - 1)г. (2.4)
При ап < 0 ионы не поглощают, а излучают колебания, и поэтому колебания, проходя через резонансную область, усиливаются (Тх > 1). Если Pi >• 1п 2, то и отраженная волна будет также усилена. В дальнейшем
Нам понадобится отношение амплитуды отраженной волны к падающей
С учетом фазы. В работе 14 эта величина была определена методом Цваана:
Ri = (е* - 1); (2.5)
Здесь фаза отсчитывается от резонансной точки, т. е. падающая и отраженная волны берутся в виде
Z
Ф ~ ехр ( ± г ^ к\ dz j. h
Так же как и в равновесной плазме, отражаются колебания, падающие со стороны меньшего магнитного поля; колебания, распространяющиеся в обратном направлении, проходят через резонанс без отражения. Коэф' фициент усиления не зависит от направления распространения колебаний.
Заметим, что при ап > 0 ионы поглощают энергию колебаний, поэтому потенциальные колебания наряду с непотенциальными можно использовать для нагрева ионной компоненты плазмы31.
|
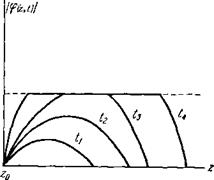
Рис. 6. Усиление колебаний, падающих со стороны меньшего магнитного поля. Обозначения те же, что на рис. 5. |
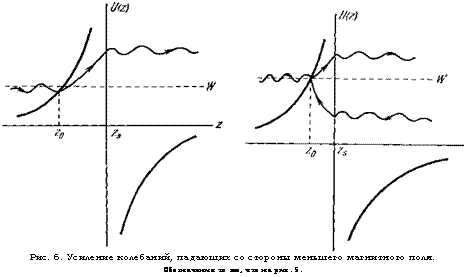 Представляет интерес проследить за процессами, приводящими к усилению прошедшей и отраженной волн. На рис. 5, 6 изображен потенциал.
Представляет интерес проследить за процессами, приводящими к усилению прошедшей и отраженной волн. На рис. 5, 6 изображен потенциал.
Рис. 5. Усиление колебаний, падающих со стороны большего магнитного поля. и и) = (тр/тп-) П2апа/(а — псо( (г)) — потен- циальная энергия в уравнении Шрёдингера, эквивалентном (2.2); — Л^о)2/о)ре — полная
Энергия, остальные обозначения те же, что на рис. 3 и 4.
Входящий в уравнение Шрёдингера, эквивалентное (2.2). Из сопоставления их с рис. 3 следует, что в неравновесной плазме (а„ < 0) потенциал меняет знак (как и ранее, считаем dHjdz < 0). Рассмотрим колебания, падающие на резонансную точку со стороны большего магнитного поля. Такие колебания сначала попадают на обычную точку поворота z0 (см. рис. 5) [31]). В области непрозрачности (z0 •< z < zs) их амплитуда нарастает
Z
Экспоненциально exp (i j k^dz^ , и в точке zs превышает началь
Ную на множитель ~p~1/2ePi/2. Однако поток энергии остается неизменным вплоть до точки zs, где колебания отбирают энергию у ионов. Количество энергии, отданной ионами, оценим с помощью (2.1), положив t да (U||da)j/dz)_1/2. Из очевидного соотношения Т да и0Уц j8WjlSt получаем 71, = е$1/2; здесь бЖ,- — энергия, отданная одним ионом, *51 = = V0EV4я — поток энергии в области слева от zs, Е — амплитуда
колебаний в точке Ув = юре/к± — их групповая скорость при | г — г31 - V —► оо. Рис. 6 иллюстрирует процесс отражения колебаний, падающих со стороны меньшего магнитного поля. Коэффициент отражения можно оценить изложенным выше способом.
В) Немонотонное магнитное поле. С уменьшением градиента магнитного поля в резонансной точке коэффициенты усиления и отражения колебаний возрастают (см. (2.3) — (2.5)). Так как в адиабатических ловушках магнитное поле имеет минимум в центре системы, для колебаний с со « & гшп коэффициенты Т^ 7?! должны быть максимальны. Однако их вычисление в этом случае сопряжено с значительными трудностями. Во-первых, адиабатическое волновое уравнение при немонотонном профиле магнитного поля не сводится к стандартным, во-вторых, при -> —>-гт1П само его использование оказывается незаконным. Действительно, в соответствии с правилом обхода Ландау, в спадающем магнитном поле резонансная точка должна обходиться в комплексной плоскости сверху и в нарастающем снизу. Поэтому при резонансе вблизи экстремума, когда резонансные точки встречаются парами, мы должны обязательно пройти между ними. С приближением к длина затухания модулированных пучков, генерируемых в резонансных точках, может оказаться больше расстояния между и 2т|а. В этом случае при построении решения мы обязательно попадем в область, занятую пучками, где упрощенное адиабатическое волновое уравнение оказывается неприменимым (см. раздел 1, в)).
При больших (термоядерных) плотностях кулоновские соударения должны уширять функцию распределения ионов по скоростям. В такой плазме тепловой разброс продольных скоростей будет довольно большим (би,, ж Уц) и, следовательно, модулированные пучки должны затухать ла расстоянии порядка длины волны модуляции (см. раздел 1, в)). Тот же порядок величины имеет и размер резонансной зоны 6ге. При
I 2[32] — гт|„ | > гуз£2/з б г, « (^/г^1/2 и при | г8 — гт1 п | ^ г^3Ь2/3
8г3 л: г'/:1Ь^3; здесь принято
//(2) = ят|п[1+(--'1>|п )2).
Поэтому мы будем считать, что приближение к 2т1а лишь расширяет резонансную зону, делая резонансное взаимодействие более интенсивным *).
Оценим коэффициент усиления колебаний С СО Ж П(х>1 т1п. Количество энергии, отобранной колебаниями у ионов, пропорционально квадрату амплитуды колебаний в резонансной точке (см. (2.1)). Амплитуда возра-
Г
Стает в области непрозрачности ~ехр (| 1т. В результате пока - гатель экспоненты в выражении для коэффициента усиления оказы-
Вается равным р4 = | 1т ку{ йг (см. (2.3)). При резонансе в минимуме
Магнитного поля приближенные оценки дают р, ж С (к^Ь^ (т^т^1'2; :;десь С — величина порядка единицы. Это приближенное выражение можно использовать при | —2т|„ | Ь1 ап |1/2 со,^/исо(. Если
| 2а — гт1 „ | Э - ^1 I ап |1/2 С0р(/7гс0г, то области, в которых колебания отличаются от плоских волн, разделены. В этом случае каждый из резонансов может рассматриваться по отдельности, как резонанс в монотонно меняющемся магнитном поле.
Г) Колебания, нарастающие во времени. В ограниченной плазме усиление в резонансной области приводит к установлению колебаний, нарастающих во времени (Im со = у > 0). Оказывается, что в простейшем случае линейно меняющегося магнитного поля коэффициенты усиления и отражения (2.3) — (2.5) не зависят от величины инкремента у. Однако, несмотря на это, при у > 0 процесс перекачки энергии от ионов к колебаниям происходит по-иному. Прежде всего при у (6уц dcoildz)1/2 не возбуждаются модулированные пучки. Действительно, частоту нарастающих колебаний нельзя определить с точностью бо), превышающей инкремент. Поэтому, если У Ф 0, можно считать, что в возбуждении пучков одновременно участвует много волн. Из (1.16) следует, что при у (6уц dm,-/dz)1/a интерференция должна гасить модулированные пучки. Соответственно заштрихованная область на рис. 2 опускается ниже действительной оси, л на всей оси можно использовать адиабатическое волновое уравнение, учитывая неоднородность магнитного поля параметрически. (Сравнить с колебаниями в столкновительной плазме; см. гл. I, раздел 2, а)). Этот результат можно также получить, рассмотрев движение отдельного иона. Действительно, при у ^ (биц doij/dz)1/4 ион не «чувствует» неоднородности магнитного поля, так как амплитуда колебаний меняется раньше, чем он уйдет из резонансной зоны.
Оценивая энергию, отдаваемую ионами нарастающим колебаниям, из всей предыстории следует учитывать ближайший интервал бt « у-1, поскольку в более ранние моменты времени амплитуда колебаний экспоненциально мала. В силу неопределенности частоты нарастающих колебаний резонансная зона размывается на расстоянии порядка 6zs л; да у (d(Oi/dz)zLzs• Число частиц, находящихся в ней, »n06zs, а энергия,
Отдаваемая ими в единицу времени, mna8zsWi да пгап(л{ (dwi/dz)~1E2/in. Эта величина не зависит от инкремента (оценка для случая у = 0 была сделана выше). Если в окрестности резонансной точки магнитное поле меняется по нелинейному закону, то с ростом у резонансное взаимодействие ослабляется. Так, например, в предельном случае резонанса в минимуме магнитного поля показатель экспоненты р4 в выражении для коэффициента усиления, определенный в предыдущем разделе, можно использовать лишь при у ((Dpi/a);) | ап/п |. В обратном предельном случае следует сделать замену р4 -v р4 [со/>|/(согу)1'2] | aJn I1'2.
Устойчивость циклотронных колебаний в магнитных ловушках, а) Границы, отражающие колебания. В адиабатических ловушках магнитное поле возрастает от центра к краям системы, что ограничивает движение заряженных частиц вдоль магнитного поля. В ограниченных системах эволюция произвольных возмущений приводит в конце концов к установлению собственных колебаний. Последние можно считать составленными из падающей и отраженной волн. Если система симметрична относительно минимума магнитного поля (z =0), а колебания отражаются как от резонансной области, так и от границы плазмы, то условие согласования падающей и отраженной волн имеет вид
Zs zb
Ri exp 12i j dz) + Rb (2i j k{{ dz^j = ± 1; (2.6)
О a
Здесь - f 1 соответствует симметричным модам, —1 — антисимметричным, - ffi — коэффициент отражения от резонансной области (2.5), Rb — коэффициент отражения от границы плазмы z = zb. Если плотность плазмы на границе меняется достаточно резко, дАгц (zb) 1 (Агц (zb) да к±и>1шре (zb),
2 УФН, т. 110, вып. 3
А. — характерный масштаб изменения плотности), и на расстоянии Ь от границы помещена металлическая стенка, то Иь = е-!Р, где о = = агЫ# [25/(1 —В2)], В = [Агц (гь)/А:^] сЛ (к^Ь). Из этого выражения следует, что отражение от границы плазмы изменяет фазу, но не амплитуду колебаний. Здесь и в дальнейшем поле магнитной ловушки аппроксимируем выражением Н (г) = Н0 [1 + №;)].
В работе 33 указано, что при плавном изменении плотности на границе а&ц 1 колебания, падающие на границу, должны поглощаться без отражения (Я*, = 0). Действительно, вдали от резонансной области в адиабатическом волновом уравнении (2.2) можно не учитывать вклад ионов, при этом колебания переходят в замагниченные электронные лэнгмюровские с &ц (г) да к±(й/шре (г). Волновой пакет, составленный из таких колебаний, двигаясь к границе, т. е. по направлению, в котором плотность плазмы падает, уменьшает фазовую (групповую) скорость ш/Агц да юре/к±. Когда она по порядку величины сравнится с тепловой скоростью электронов, колебания поглотятся резонансными электронами.
С другой стороны, в не слишком длинных системах, гь < Ьи с резкой границей плазмы, можно не учитывать отражения от резонансной области. Дело в том, что, как показано в работе 16, колебания, отраженные от резонансной точки, запаздывают на время / да здесь Ье =
= (Я-1 dHldz)гLгs, Г0 = (йРе/к±. Если выполняется условие уЬ8/У0 <^1, то колебания, отраженные от границ, за это время усилятся в большей степени.
|
О |
 Рассмотрим сначала колебания плазмы с резкой границей, когда отражение от резонансной области (первое слагаемое в (2.6)) можно не учитывать. Из (2.6) находим
Рассмотрим сначала колебания плазмы с резкой границей, когда отражение от резонансной области (первое слагаемое в (2.6)) можно не учитывать. Из (2.6) находим
(2.7>
Здесь р — целое число. Если изменение магнитного поля в пределах системы достаточно мало, 8Н/Н = (zb/Z,,)a (шрг/(ог) | аJn I1'2, то магнитное поле может считаться однородным. При этом из (2.7) получаем Im со = = Yo да (Opi | a. J2n I1/2. В обратном предельном случае (zb/L,)2 ((ьpj/toj) | а jn I1/2 резонансная область занимает малую часть системы 6zs/zb да (yo/zb) (d(ьj/dz)zLzs (см. предыдущий раздел). Поскольку в резонансной области процесс перекачки энергии от ионов к колебаниям происходит с той же интенсивностью, что и в однородном поле, инкремент колебания должен уменьшиться по сравнению с "у0 в отношении б zjzb - Действительно, при (zb! Li)2 ((opi/cot) | а Jn I1/2 из (2.7) находим
(см. 30' **)
У да (я/4) (а Jn) [L!(zs — zb)
Это выражение для инкремента можно получить и иным способом. Рассматриваемые колебания близки к замагниченным электронным лэнгмю - ровским, групповая скорость которых равна = юре/к±. За одно прохождение между границами, т. е. за время 1Ь = 2гь/У0, их амплитуда в соответствии с (2.3) увеличится на множитель Т = е&1 (в параболическом магнитном поле колебания дважды переходят через резонанс). Инкремент находим из условия у% = §1. Он возрастает с уменьшением г8. Предельное значение можно найти, взяв
|
|
Б) Границы, поглощающие колебания. В плазме с плавной границей (Яь = 0) собственные колебания устанавливаются за счет отражения от резонансных точек. Примерный вид колебаний изображен на рис. 7. Между резонансными точками имеются две волны спадающей амплитуды, распространяющиеся навстречу друг другу, за резонансными точками,— убегающие волны. Спадание амплитуды в области | ъ | < связано
|
Рис. 7. Нарастающие собственные колебания в поле магнитной ловушки при диссипативных граничных условиях. Обозначения те же, что на рис. 5 и 6. |
С тем, что собственные колебания, рассматриваемые нами, нарастают во времени. Если выполняется условие 1т Агц = (у/ш) Ие &ц, то в области | г | -< где ионы не взаимодействуют с колебаниями, их амплитуда не меняется п^и распространении, поскольку временное нарастание компенсируется пространственным спаданием. Так как волны, убегающие на границы, уносят энергию, а колебания при этом нарастают, их следует отнести к классу колебаний с отрицательной энергией 35> зв.
Если 01^1» то
Го
7?! « —г ехр ^2г ^ Агц,
Г8
И (2.6) можно привести к виду}
*0
2 TOC o "1-5" h z | Агц с? г = (р + 1/2) л. (2.8)
О
Отсюда»находим, гчто колебания неустойчивы 141
(0 = „а)го___^^1 + 1 |а„|1/2. (2.9)
И п(010 п тог о т 1 '/ ' '
В неустойчивом состоянии параметры плазмы таковы, что у ^ ©рг/шг 0, в то время как при условии отражения колебаний от границ у > ш^/ш,- 0- С уменьшением (увеличением неоднородности) инкремент сначала возрастает, что объясняется сокращением области локализации колебаний. Однако при этом падает и коэффициент отражения, так как р,
< С (тПе/т.^2 (см. раздел 1, в). Если Ь1 /сд1 (т1/те)1/2, т0 Р1 <С ^
2*
При этом колебания проходят через резонансную область практически без отражения (и без усиления), что делает существование собственных колебаний невозможным. Отсюда находим, что неустойчивость существует лишь при Ьх з[33] Aq1 (т^тпе)1!2. Эта оценка критического значения согласуется с результатами исследования (2.6) 14:
Lier = (п/к±) [(р 1/2) In 2-| а„ |-1 (milme)]1!2; (2.10)
Здесь, как и ранее, fcj_ > г^1, | an | < 1. Частота колебаний при L, = Licr
Равна (щ = n(щi D - f (р 1/2) (л2/4) In 2 | а„ | (щ%Jn(щi 0.
Эти результаты относятся к плазме низкой плотности шрг/шг ^ 1.
Численные расчеты показывают, что условие стабилизации циклотронных колебаний слабо меняется вплоть до «термоядерных» плотностей ((шрг/шг)2 « 103) 14. При (щpil(ыi ■у' 1, наряду с циклотронными, появляются колебания, на развитие которых магнитное поле вообще не влияет, так как их инкремент у > шг 33. Хотя циклотронные колебания имеют меньший инкремент, они в некоторых отношениях более опасны, поскольку их, например, труднее стабилизировать примесью холодной плазмы 37. В заключение заметим, что проведенное выше условие стабилизации LJr, (mj/me)1/2 (kd ^ r^1) может оказаться трудно выполнимым в реальных системах, так как уже при 1ц1г1 та 25 должны начаться потери частиц из ловушки из-за несохранения магнитного момента (см., например, 38).
В) Эволюция возмущений во времени. Рассмотрим эволюцию возмущения, которое при t = 0 имело вид б-функции. Такое возмущение будем называть элементарным. В соответствии с 1S, асимптотика коротковолновой, квазиклассической части возмущения имеет вид *)
Г *
Ф;0 (z, t)^C (z, z0, I) exp [—tыrt-f-t sgn (z —z0) J dz’k\ (z', to)J; (2.11)
Здесь С (z, z0, t) — медленно меняющийся предэкспоненциальный множитель, а частота со определяется уравнением
Z •
Ј = sgn(z — z0) j dz [dfc||(z', ш)/д(о], (2.12)
20
Являясь функцией протекшего времени t, точки наблюдения Z И ТОЧКИ возникновения элементарного возмущения z0. Поскольку величина доа/дк определяет скорость распространения квазиклассических возмущений, физический смысл (2.12) очевиден.
Примем для простоты линейный закон изменения магнитного поля H (z) = Но [1 — (z/L)]. С помощью (2.11), (2.12) находим частоту и комплексную фазу колебаний:
(1-т?)+[<“"<2-,3> ® (*.*.<)=—« + ■£• <*—*.) + (2-М)
Здесь учтена та часть элементарного возмущения, которая распространяется направо (z > z ). В области z < z0 возмущение эволюционирует аналогичным образом.
Из (2.14) следует, что колебания нарастают, если выполняется условие
- г0) (Уо* — (г — г0)) < где 1Г = Ь (&)„г/&)г) [ 2ап/п I1/8. При
|
(г |
![]() Нарастание прекращается и вместо одной комплексной частоты с у > О появляются две действительные. При t и одна из этих частот стремится к локальной циклотронной частоте со да пшг (г) (и^/Зл;*), другая —
Нарастание прекращается и вместо одной комплексной частоты с у > О появляются две действительные. При t и одна из этих частот стремится к локальной циклотронной частоте со да пшг (г) (и^/Зл;*), другая —
|
Рис. 8. Траектория частоты ю (г) возмущения, имевшего в начальный момент вид 6-функции. Координата г (г > г„) фиксирована; магнитное поле меняется по линейному закону Н (2) = Но [1 — (г/1.)]. |
![НЕРАВНОВЕСНАЯ ПЛАЗМА подпись:
рис. 8. траектория частоты ю (г) возмущения, имевшего в начальный момент вид 6-функции. координата г (г > г„) фиксирована; магнитное поле меняется по линейному закону н (2) = но [1 — (г/1.)].](/img/556/image278.gif) К циклотронной частоте в точке, где возникло возмущение, со да пшг (г0) —
К циклотронной частоте в точке, где возникло возмущение, со да пшг (г0) —
— (ир4/2л<). Траектория частоты на плоскости комплексной переменной
|
Рис. 9. Эволюция возмущения, имевшего в начальный момент вид 6- функции. Магнитное поле меняется по линейному закону. |
Приведена на рис. 8. Общая картина эволюции элементарного возмущения дается рис. 9.
За время нарастания колебаний их амплитуда увеличивается на множитель = еР1/2. Действительно, к моменту времени Ь ~ Ьт аргумент логарифма в (2.14) получает приращение» —л и затем остается постоянным.
Таким образом, временной коэффициент усиления первоначального возмущения оказался равным пространственному коэффициенту усиления возмущения, периодического во времени, при его прохождении через точку циклотронного резонанса. Это совпадение не случайно. Действительно, при Ь > и частота колебаний в точке ъ лежит в интервале ио); (г0) > со > по}{ (г). Такие колебания, двигаясь из г0 в г, должны обязательно пройти через точку циклотронного резонанса.
Плазма может считаться практически устойчивой, если временной коэффициент усиления близок к единице. С другой стороны, было показано, что при поглощении колебаний на границе плазмы это условие обеспечивает устранение неустойчивых собственных колебаний.
Использованное нами выражение для ср7о (г, 2) учитывает волны, убегающие от точки г0 (см. (2.11)). Если колебания отражаются от границ, то при I да да й должны появиться отраженные волны. В работе 15 показано, что при £ > £/Уо > Iь появляются также волны, отраженные от точки циклотронного резонанса (обычно характерный масштаб изменения магнитного поля Ь больше гь). Фактически за несколько отражений успевают установиться собственные колебания. При этом следует использовать результаты предыдущих разделов. Таким образом, оба подхода
к исследованию устойчивости плазмы (рассмотрение эволюции возмущений во времени и анализ собственных колебаний) согласуются и взаимно дополняют друг друга.
Более подробное исследование эволюции первоначальных возмущений произведено в работе 15. В частности, найдено, что и в немонотонном магнитном поле временной и пространственный коэффициенты усиления совпадают друг с другом. Прослежена эволюция пространственно-периодических возмущений и возмущений в виде волновых пакетов. Показано, что в неустойчивых неоднородных средах волновой пакет может распасться на образования, дальнейшую эволюцию которых нельзя описать в терминах волновых пакетов.
Г) Циклотронные колебания плазмы с горячими электронами. В предшествующем рассмотрении электроны считались холодными (ve/vt
< ((Bpe/msJ/Ar^rj, где к± ^ Гг1). Для того чтобы составить представление о характере неустойчивости в плазме с горячими электронами, полезно сначала рассмотреть более простой случай колебаний в однородном магнитном поле. В однородных средах колебания имеют вид плоских волн g-iiot+ikr Зависимость со (к) определяется дисперсионным уравнением, которое для циклотронных колебаний в плазме с горячими электронами имеет вид (см., например, 36)
Е (to, k) = l — (-^2------- fian ■ +*k;U + iynTr? T - ) =0; (2.15)
' ' V к I пы, (w— пы,) kZvi 1 *ц 1 «в / '
Здесь е (со, к) — диэлектрическая проницаемость плазмы.
В нулевом приближении по | Im e/Re е | 1 из (2.15) находим
, “р> Г / к 2 , I wPe 2
Если ап < 0, то энергия этих колебаний, определяемая по формуле W = = (1/8я) со {де/дю) | Е |2, отрицательна (см., например, 38). Электроны, тепловая скорость которых равна фазовой скорости волны, поглощают энергию (бесстолкновительное поглощение Ландау). Этот эффект, учитываемый малой мнимой частью е, приводит к раскачке колебаний36- w. По существу, рассматриваемая неустойчивость отличается от неустойчивости с диссипативными граничными условиями (см. раздел б)) лишь тем, что поверхностная диссипация у границы плазмы заменяется объемной.
Если магнитное поле неоднородно и его изменение в пределах области, занятой плазмой, достаточно велико,
2-1-1
То для рассматриваемых колебаний будут характерны резонансы с циклотронным вращением ионов. При циклотронном резонансе в неравновесной плазме (ап < 0) энергия излучается, что должно приводить к затуханию колебаний с отрицательной энергией. В силу этого волновой пакет, составленный из колебаний с отрицательной энергией, существует лишь до тех пор, пока не дойдет до точки циклотронного резонанса. Таким образом, следует ожидать (см. 30), что в плазме с горячими электронами неустойчивые собственные колебания будут отсутствовать, а сама неустойчивость будет проявляться в виде нескоррелированных между собой вспышек. В магнитном поле, меняющемся по параболическому закону, Н (г) = = Н0[ 1 + (г2/£®)], время существования вспышки
А, - _1 Ь1 Г. , / шреГ, 2 11/2
Дг<соР1 — [1 + (__) ] .
Заметим, что в окрестности минимума магнитного поля, вообще говоря, ВОЗМОЖНЫ неустойчивые собственные колебания С 0) < ntyi Ш1п, для которых не выполняется условие циклотронного резонанса. Однако достаточно сильная неоднородность магнитного поля *£ гг ((о4/а)рг) |ап [ /и-1/2 устраняет и эти собственные колебания. В математическом отношении задача о колебаниях плазмы с горячими электронами в неоднородном магнитном поле близка к задаче о колебаниях течений сплошной среды, движущейся со скоростью, переменной в направлении поперек течения. Подробное изложение этого вопроса можно найти в обзорной работе 41 (см. также 30> 42).
Д) Анизотропная неустойчивость. Для магнитных ловушек с низкой плотностью плазмы (шрг < а);) характерны анизотропные распределения ионов по скоростям, при которых средняя энергия теплового движения ионон в направлении поперек магнитного поля существенно превышает продольную. Анизотропия распределения, так же как и конусность, может быть причиной раскачки циклотронных колебаний. Для анизотропной неустойчивости характерно, что даже при большой анизотропии неустойчивы лишь колебания с со < пш(, а колебания со > п шг затухают. Это положение иллюстрируется видом мнимой части диэлектрической лроницаемости (см., например, 36):
^2 ^ апР°{щ)а* (ун>)
17ц = ((0 — пю^/кц, (2.16)
Здесь (уц) — функция распределения ионов по продольным скоростям, которая берется при Уц = (со — п(о{)/кц,
Оо
Ащ == 2л | (/с1у^/о)1) (ух),
О
Магнитное поле, как и в (2.15), считается однородным.
Знак 1т е характеризует баланс энергии в колебаниях. Ионы отдают энергию, если 1т е < 0. Первое слагаемое в (2.16) учитывает поперечные смещения ионов в поле волны. Оно может быть отрицательным для конусных распределений, когда а„ < 0. Второе, посредством которого учитываются продольные смещения, преобладает при достаточно малом тепловом разбросе по продольным скоростям. Если распределение по Уц спадает монотонно (отсутствуют пучки), то оно становится отрицательным при со < пм;. В неоднородном магнитном поле могут одновременно присутствовать как область раскачки, так и область затухания. Поэтому неустойчивость за счет анизотропии возможна лишь в том случае, когда влияние области раскачки преобладает.
Если магнитное поле меняется монотонно и его изменение в пределах системы достаточно велико,
То коэффициент усиления (ослабления) циклотронных колебаний при прохождении через резонансную область дается выражением
Оо
Т! = ехр [ | йз (у/у0)] ;
— оо
Здесь у = —1т е,/(д Ие е,/ди>) — локальный инкремент (временной коэффициент усиления), Ие е « 1 — [(а)ре/ю) Агп/А:]2, У0 « соре/к± — групповая скорость колебаний; неоднородность магнитного поля и плотности в этих выражениях учитывается параметрически. Вычисления дают Тх = TnTVi, где Тп — еР‘/2 (см. (2.3)), а для Т1г имеем
R.2 = expfЈ-^*x-^r(—с}. (2.17)
L 2 »ij | (ш,)г | L (щpe (<ыj)z I г Jz=zs)
Из (2.17) следует, что для усиления колебаний за счет анизотропии необходимо выполнение по крайней мере одного из неравенств Н'гН"гг < 0Т H'z (ain)z > 0, Нг (пIq)z < 0. Поясним эти условия.
Амплитуда колебаний меняется внутри резонансной зоны, где Im е ф= Ф 0. Из (2.16) следует, что размер резонансной зоны равен да | |.
Если выполняется первое неравенство, то область усиления колебаний (о) < n(щt (z)) имеет больший размер, чем область ослабления (со > пш,- (z)). Продольное движение ионов в поле колебаний определяется п-й цилиндрической гармоникой в разложении плоской волны (ср. с разделом 1, а). Поэтому второе неравенство обеспечивает большую интенсивность резонансного взаимодействия в области усиления (Im е ~ ащ). Наконец* третье учитывает действие нескольких эффектов, поскольку с увеличением плотности возрастает число резонансных частиц ~и0, сокращается размер резонансной зоны ~Дг ~ Агц ~ «01/2, ослабляется резонансное взаимодействие Im е ~ (и — тш,) АгцУц ~ п-1/2, возрастает продолжительность взаимодействия, так как колебания замедляются, Va ~ л~1/2.
В магнитных ловушках размеры области занятой плазмой, как правило, меньше характерного масштаба изменения магнитного поля L. В этом случае преобладает эффект, связанный со второй производной магнитного ПОЛЯ, причем, поскольку НгНгг > 0, при прохождении через область циклотронного резонанса колебания ослабляются. Исключение представляют колебания с со да пшг mIn, для которых w < тшг (з) и поэтому область поглощения вообще отсутствует. Такие колебания и будут раскачиваться при условии отражения от границ плазмы. Если колебания поглощаются на границах, а распределение ионов хотя и анизотропно, но монотонно по поперечным энергиям, то неустойчивые собственные колебания установиться не могут. Действительно, при диссипативных граничных условиях собственные колебания должны быть локализованы между точками циклотронного резонанса (см. раздел б)). Однако если эти точки разнесены (удалены от центра ловушки), то резонансное взаимодействие должно приводить к ослаблению колебаний. Можно также показать, что неустойчивые собственные колебания невозможны и в плазме с горячими электронами.
Е) Дрейфово-циклотронная неустойчивость. Если плотность плазмы меняется в направлении поперек магнитного поля, то дрейф электронов в скрещенных полях (электрическом поле волны и постоянном магнитном) приводит к разделению электронного и ионного зарядов. Этот эффект можно учесть, если в (2.2) ввести дополнительное слагаемое к±х (со/сое) <р, где х = (k^V«o)/&iwo- Анализ измененного уравнения показывает, что уже при малой неоднородности хгг да 10 "2 — 10-3 появляются неустойчивые колебания, сильно вытянутые вдоль магнитного поля (дрейфовоциклотронная неустойчивость с &ц - v 0) 43. Такие колебания не могут поглощаться у границ плазмы, так как для них любая граница является резкой, аАгц —V 0 (см. раздел б)). По аналогии с результатами, полученными в этом разделе, следует заключить, что неоднородность магнитного поля может лишь уменьшить инкремент дрейфово-циклотронной неустойчивости, не приводя к ее полной стабилизации. В реальных условиях изменение инкремента должно быть небольшим 44.
Основной результат, полученный в разделе 2, можно сформулировать следующим образом. Увеличение неоднородности магнитного поля оказывает стабилизующее воздействие на циклотронную неустойчивость. Будет ли при этом уменьшаться инкремент неустойчивых колебаний или произойдет их полная стабилизация, зависит от конкретных условий.
Обращаясь к экспериментальным данным, характеризующим устойчивость циклотронных колебаний в магнитных ловушках, заметим, что ввиду сложности реальных систем, приводящей к необходимости одновременного учета множества факторов (электрическое поле, влияние торцов, сложная форма силовых линий), эффект влияния неоднородности магнитного поля на устойчивость плазмы к настоящему времени не исследован. В то же время имеются четкие указания на улучшение устойчивости плазмы при увеличении неоднородности магнитного поля (см., напримемер, 45).
ПРИЛОЖЕНИИ
При циклотронном резонансе в неоднородном магнитном поле обмен энергией между колебаниями и заряженными частицами осуществляется посредством нозбуж - дения модулированных пучков. Сходным образом протекают п другие процессы, приводящие к обмену энергией между колебаниями и плазмой, если их область действия ограничена малой областью пространства. Так, например, при взаимодействии колебаний с потоком заряженных частиц, движущихся со скоростью v0 (г), меняющейся в пространстве, модулированные пучки будут возбуждаться в точке rs, где фазовая скорость колебаний w/k совпадает со скоростью потока Vo (rs). В этом случае допплеровское смещение частоты kv0 (г) играет ту же роль, что и сдвиг на пи>, (г) для циклотронных колебаний *.
Остановимся теперь на взаимодействии между колебаниями и заряженными частицами при резком (скачкообразном) изменении скорости частиц. Рассмотрим упрощенную модель. Пусть вдоль OZ распространяется плоская волна Е = Eie~ и в том же направлении со скоростью Vo (z) движется поток заряженных частиц. Предположим, что в окрестности некоторой точки zs скорость потока достаточно резко изменяется на малую величину "С ио (zs)- Из уравнения движения
Vi = (eEJm) e~l(ьt+lh^t'> (П.1)
Находим
T
Vi = (eEJm) J dt'e~l<дi'+lhz<f,); (П.2)
— oo
Здесь z (t) — траектория частицы.
Введем под интеграл 1 =[—+^о(*')]/[—ю + АиоЮ] и проинтегрируем по частям
T
F Dt'{-)-пе-<ш'+»мп ]. (П. з)
Т Lw — kv0(t) J (w— kva (t ))2 J '
— oo
Второе слагаемое в (П. З) учитывает предысторию движения частицы, которая существенна только при наличии ускорения. Если зависимость ускорения от времени имеет вид 6-функциИ, то из (П. З) получаем
V, = .1*1. Г------------------- .---------- g-iat+ikzlt)________________ tjcApg (ts)__ l03ts+lhz(ts) 1 ■ /П
Ui m L a>-ki>0(t) e (co_bo(is))ae J.
Здесь Avt> (ts) — скачок скорости в точке zs = г (ts).
Из (П. 4) следует, что в точке zs частицы получают приращение скорости (второе слагаемое). Это приращение затем переносится со скоростью i>0 (z)- Иными словами, в точке zs возбуждаются модулированные пучки Энергия, необходимая для этого, отбирается у колебаний Таков механизм бесстолкновительного поглощения (аномальный скип-аффект), рассмотренного в работе п. В этой работе исследовалось поглощение на границе плазмы, отражаясь от которой частицы резко изменяют свою скорость (зеркальное отражение, диффузионное отражение).
При наличии теплового разброса по скоростям колебания, связанные с модулированными пучками, затухают в пространстве. По аналогии с (1.9) легко найти, что при максвелловском распределении затухание происходит по закону ~ ехр [—а (г — zs)2/3]. Эта характерная зависимость была впервые] получена в работе 48, где, в частности, рассматривалось распространение колебаний, возбуждаемых на резкой границе плазмы. Она получает естественное объяснение в терминах модулированных пучков. Более подробный анализ явлений, возникающих у резкой границы плазмы, можно найти в работе 1о.