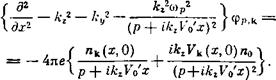ФИЗИКА ПЛАЗМЫ

ОБ УСТОЙЧИВОСТИ ЭЛЕКТРОННОГО ПОТОКА С ГРАДИЕНТОМ СКОРОСТИ

В. М. Костин, А. В. Тимофеев

На простейшем примере электронного потока с линейным профилем скорости в •сильном продольном магнитном поле изучаются явления, возникающие при относи­тельном скольжении слоев плазмы. Показано, что в рассматриваемом случае плазма устойчива, а начальные возмущения затухают во времени по степенному закону /-* (а > 0).

Введение

В работе рассматриваются колебания плоского электронного потока, движущегося вдоль магнитного поля со скоростью, меняющейся линейно в поперечном направлении. Предполагается, что магнитное поле достаточ­но велико и поэтому препятствует поперечным движениям плазмы в коле­баниях. Устойчивость такого наиболее простого течения исследовалась Гаррисоном [*]. Более сложные системы рассматривались в ряде других работ (см., например, [2~4]). Авторы этих работ пришли к заключению, что скольжение слоев плазмы в течениях с переменной скоростью являет­ся дестабилизирующим фактором. Неустойчивость, обнаруженная ими при достаточно большом градиенте скорости, получила название 8Іірріп£-не- устойчивости.

В то же время влияние скольжения слоев сплошной среды на ее коле­бания изучалось в теории плоскопаїраллельньїх течений идеальной жидко­сти (см., например, [5]), а также в связи с желобковымн колебаниями раз­реженной плазмы в электрическом поле [6’7]. В этих случаях было показа­но, что для 'простейших профилей скорости такое скольжение приводит к устранению всех незатухающих колебаний, т. е. к стабилизации потока. (В гидродинамике это утверждение составляет содержание теоремы Ре - лея.) Довольно общее доказательство этого утверждения, данное в [7], может быть перенесено на рассматриваемую систему. Однако оно относит­ся лишь к коротковолновым (квазиклассическнм) колебаниям, локализо­ванным во внутренней части плазмы.

В настоящей работе исследуются колебания с произвольной длиной волны. Найдено, что при каждом значении кт (кг — компонента волнового вектора вдоль магнитного поля) имеется по два нейтральных собственных колебания, фазовая скорость которых совпадает со скоростью потока соответственно на левой и правой его границах, а мнимая часть частоты в гидродинамическом приближении равняется нулю. Заметим, что в слу­чае покоящейся плазмы для каждого значения кг имеется - полный набор собственных колебаний, по которым можно разложить возмущение с про­извольным профилем поперек магнитного поля.

В рассматриваемой задаче собственные функции не составляют полной системы. Поэтому, следуя [6 8,э], где изучались аналогичные ситуации, мы используем метод преобразования Лапласа для того, чтобы непосредствен­но проследить за судьбой первоначальных возмущений. Как и в указанных
выше работах, оказывается, что элементарными возмущениями, образую­щими полную систему, являются так называемые модулированные. пучки (аналог волн ван Камлена), движущиеся с локальной скоростью плазмы, они описываются решениями с разрывной производной. Произвольное возмущение, составленное из таких пучков, с течением времени деформи­руется и расплывается вдоль магнитного поля, что приводит асимптотиче­ски к степенному закону затухания Г41 (0 < а < 3/г)- Таким образом, вы­вод Гаррисона о неустойчивости течения с линейным ирофилем скорости представляется неверным. Нами указываются математические ошибки, которые привели к такому заключению.

При решении временных задач методом преобразования Лапласа пред­полагается, что возмущения возникают мгновенно при £ = 0. Нами пока­зано, что лоток, движущийся с (Переменной скоростью, «резонирует» на резкое включение возмущения. В результате в некоторых случаях изме­няется закон затухания (величина а). Этот эффект не учитывался в пре­дыдущих работах (см. [6,в]).

1. Основные уравнения

Рассмотрим колебания электронного потока, скорость которого меня­ется в поперечном направлении, в простейшем случае. А именно, предпо­ложим, что поток по плотности однороден и движется вдоль однородного и достаточно большого по величине магнитного поля. Нетрудно показать, ЧТО при выполнении условий (Оя 0)р, 0)Н Уо' можно не учитывать смещения электронов поперек магнитного поля. Здесь о)н — электронная циклотронная частота, ыр — плазменная частота, — градиент скорости потока. Будем считать, что поток заключен между двумя проводящими поверхностями, отстоящими на расстоянии 2а, и что его скорость меняется по линейному закону У0(х) = Уо'х (—а < х < а). Ось Ох направим пер­пендикулярно ограничивающим поверхностям, ось 0г вдоль магнитного поля, параллельно им* Очевидно, что с уменьшением градиента скорости потока колебания такой системы переходят в обычные ленгмюровские.

Мы хотим проследить за временной эволюцией произвольного началь­ного возмущения. Для этого, как обычно, применим метод преобразования Лапласа. Поведение системы будем описывать при помощи линеаризован­ного по малым возмущениям кинетического уравнения и уравнения Пуас­сона. Из этих уравнений нетрудно найти

SHAPE \* MERGEFORMAT

(2)

Из этих выражений следует, что эффекты, связанные с конечной величи­ной температуры электронов, существенны не только при |s| ^ 1, но так« же и при |s| 1, если —Зя/4 < arg s < —л/4. В остальном секторе

Комплексного переменного s переход к асимптотике приводит к обычным гидродинамическим выражениям

(3)

Здесь ^к(^О) —соответственно начальные возмущения плотно­

Сти - и скорости плазмы.

Для того чтобы найти решение неоднородных уравнений (1), (3), ис­пользуем функцию Грина в следующем представлении:

/

£р, к (я) &P. V.iд'o) 7 (х Хо)

(*>

?ЈkM? P.k(*o), (X > х0)

Здесь gp, к. (х) — решения однородных уравнений, удовлетворяющие гра-

Ничным условиям соответственно на правом (левом) конце интервала (—а, а). Эти функции выразим через линейно независимые решения одно­родных уравнений

(х) = Ф1. р, к (х) ф2,р. к (±а) — ф2,р, к (х) ф1,р, к (± а). (5>

Через W в уравнении (3) обозначен функциональный определитель

W (Vb, g~)

W = [ф1,р, к(а)ф2.р, к (—а) ф2.р, к(в)ф1,р. к (—в)]-

(6>

Если у однородных уравнений имеются собственные функции, удовлет­воряющие граничным условиям на обеих границах, то XV обращается в - нуль. Для таких значений р функция Грина имеет полюс. С помощью функции Грина запишем решение уравнения (1) в виде

Бри М ш'р> А, 3Дл > аг^5 :> —л/4 из уравнения (7) получаем

/ ч , г / ч/ / М*о,0) 1к2У(х0уО)п0 }

Фр. к(^)— 3 ^ХоСр^хь (х)4ле |' ------ -—— , ^. (8)

_я 4- 0 Хо (р + 1Л:2к0 дг0)2 '

.Зависимость возмущенного потенциала от времени определится, если вы­полнить обратное преобразование Лапласа:

^ а+гоо

Чк(х,<)= — ^ йрер!<Рр, К(х). (9)

Ст—гоо

2. Задача о собственных колебаниях

Рассмотрим сначала вопрос о собственных колебаниях в гидродинами­ческом приближении. Следуя Гаррисону [!], введем в однородное уравне­ние, соответствующее уравнению (3), новую функцию ф(г) = г"1/2фр, к(х), где г = х — гр/ктУъ,

Ч’"+—(1о)

Г Гй

Здесь V2 = 74 - соР2/^'2, к? = кг2 - г ку2. Помножим (10) на п|з* и про­интегрируем по слою, занятому плазмой. Учитывая граничные условия и отделяя действительную и мнимую части полученного интегрального со­отношения, находим

TOC o "1-5" h z $*Вег{|*Т + *121*12+7^1*1г}=0. (11)

—а ’ '

1тл>_( <2.т{ |ф'|2-!-^2|'|)|2-Т^ |Ф|2}= 0. (12)

—а

Если скорость плазмы меняется достаточно медленно соР2 .> 'ЬУо2 (х2 < 0), то (12) может быть удовлетворено лишь для нейтральных ко­лебаний с 1т оз = 0. Нетрудно видеть, что в предельном случае о)р2!^>

IV2 такпе колебания переходят в обычные плазменные с частотой

0)2 = 2 / /с2, к2 = кг2 + ку2 + п2 (я / 2а)2.

Более интересен вопрос о колебаниях плазмы при о)р2 < Ч^Уо2, когда ^2 > 0. (Заметим, что 2 = 4Л — о>Р2 / Уо'2 < 74-) В этом случае (12) допу­скает возможность колебаний с 1т ю ф 0. Однако для того, чтобы дока­зать, что такие колебания действительно существуют, необходимо по­строить собственные функции уравнения (10) с 1т ю ф 0. Такая попытка была сделана в [*]. При этом функции Бесселя выражались в виде 7±г.(г) = Л±г±у/,(г), где функция Р(г) бралась одной и той же для /±У, что неверно. Помимо того, в дисперсионном уравнении использовалась операция возведения в целую степень, что привело к появлению фиктив­ных корней. Все это и явилось причиной ошибочного заключения о не­устойчивости плазмы при о)р2 < 7-|Уо'2.

Ниже будет показано, что при о)Р2 < 74Уо'2 собственные функции Уравнения (10) с 1т о) > 0 отсутствуют. Из (11) следует, что для собст­венных колебаний обязательно найдется такая точка хс (— а < хс < а), в которой фазовая скорость волны совпадает с локальной скоростью плаз­мы Ке(а)/&2) = Уо'эсс. (Кег= 0). Отсюда следует, что собственные функ­ции, если они существуют, не могут обращаться в нуль более чем в двух точках. Для доказательства этого утверждения достаточно в качестве пра-
делов интегрирования в (11) последовательно подставить координаты двух соседних точек, в которых |}(г) по предположению обращается в нуль. Однако в силу монотонности профиля скорости соотношение Ие(о)/А:1) = Уц Ха а с ним и ураівпение (11) может быть удовлетворено» лишь один раз.

Рассмотрим теперь положение нулей функции г|? более детально. Про-» издольное решение (10) можно записать в виде

Ф = СД(21) + /-у(2і), (13)

Где 2і = ікі(х — ір/кгУ0'). Оно имеет точку ветвления 2і = 0. Следует за-' дать правило обхода этой точки или, что то же самое, положение разреза на плоскости комплексного переменного Для этого заметим, что, как следует из (2), гидродинамические уравнения (3), (10) даже при |з| 1

Не справедливы в секторе

— Зл /4 < аг£ 5 < — л /4 (|а^2і| > Зл / 4).

Этот сектор на рисунке заштрихован. Поэтому, если мы хотим использо-

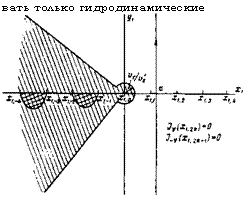Уравнения, то точку z = 0' следует обходить со стороны положитель­ных значений Re zi.

Положение нулей функции г|) на комтлексной плоскости пере­менного z 1 определяется констан­той С в уравнении (13). Траекто­рия нулей при изменении С дает­ся уравнениями

C]v(zi) +/^v(zi) =0, (14)

Dzi л

-177- = ;—, -Т *./v2(Zi). (15) dC 2sin(vn)

Если С = 0, то нули функции ф совпадают с нулями /_v(zi) и все они расположены на действитель­ной оси. Нули /v(zi) также лежат на действительной оси, причем нули функций Jv(z) и /-v(zi) чередуются

[и]. Поскольку при Imzi = 0, Rt zt > 0 имеем Im/±v(zi) = С, то нулям функции yjp, лежащим на действительной положительной полуоси, соот­ветствуют действительные значения константы С. Функции Бесселя удов­летворяют равенству J±у(21 *) =/±v*(zi), поэтому комплексно сопряжен­ным значениям С из (14) соответствуют Zi*, следовательно, достаточно рассмотреть случай Im С > 0. Уравнение (15) показывает, что при d Im С > 0 все нули с действительной полуоси Re zi > 0 смещаются в верхнюю полуплоскость. На действительную ось они возвращаются лишь прл Im С = 0. Таким образом, при ImC ^ 0 все нули, выходящие с по­луоси Im Zi = 0, Re Zi > 0, лежат в верхней полуплоскости. Однако, что­бы удовлетворить граничным условиям, два нуля функции г|? должны рас­полагаться на линии Re zt = Re k{(ix + p / kzV0') = const и, как показа­но выше, по разные стороны от действительной оси.

Проследим теперь за траекторией нулей, которые при С = 0 находятся на нижнем берегу разреза Imz, = 0, Rezi.<0. Эти нули при Im С > 0 не могут перейти в правую полуплоскость. Действительно, для этого им необходимо пересечь мнимую полуось Imzi < 0, однако на оси (14) мож­но записать С = — eivJT/_v (г/1) //v (г/1), откуда следует т. С < 0. Более де­тальное исследование показывает, что при Im С > 0 траектории нулей, выходящих с нижнего берега разреза, располагаются внутри заштрихован-

Ного сектора (на рисунке эта область нанесена двойной штриховкой), т. е. находятся в области, где неприменимы сами гидродинамические урав­нения.

Таким образом, мы показали, что в правой полуплоскости Re zt все нули лежат по одну сторону от действительной оси и, следовательно, у уравнения (10) отсутствуют собственные функции, соответствующие нарастающим и нейтральным колебаниям (Rep^O). Теперь вспомним, что уравнение (10) было получено из (3) заменой <р = г^г^г), где г = = х — ip I kzV0 Если р = —ikzV0'a, то при х = а, когда г = 0, <р обра­щается в нуль, даже если = CJV + /-v ¥= 0. Если р = ikzV0'а, то при х= —а ситуация аналогична. Для того чтобы при р = —ikzVora функ­ция ф из (13) была собственной, достаточно положить константу С = - J~v(—2iaki) / Jv(2iaki).

Таким образом, для каждого значения кг мы нашли по две собствен­ные частоты (t> = dzkzVo'a с соответствующими собственными функциями Обычно, например, в задаче о ленгмюровоких колебаниях в покоящейся плазме каждому значению кг соответствует счетное множество собствен­ных функций, по которым можно разложить (возмущение с данным кгл произвольным образом зависящее от остальных координат. Заметим, что при kia^$>i найденные нами собственные функции спадают от границы плазмы по экспоненциальному закону <р « зто выражение получе­

Но с использованием асимптотических выражений для функций Бесселя, (см., например, [и]).

Из рисунка следует, что при р = ±ikzV0'a граничные точки попадают в заштрихованную область, где необходимо учитывать эффекты, связан­ные с конечной (величиной температуры электронов (см. уравнение (1)), Под влиянием этих эффектов нули собственных функций могут сместить­ся в комплексной плоскости на расстояния порядка vT/Vo Этому смеще­нию соответствует изменение собственных частот на величины порядка кгит. Поэтому возможно, что найденные нами собственные колебания на самом деле являются нарастающими (затухающими) с малым инкремен­том (декрементом) | Im w | ^ kzvT.

Точное использование (1) в заштрихованной области затруднительно, так как внутри нее «потенциал» v2/^2, входящий в (3), заменяется на весь­ма сложное выражение (ьpzvt~2(1 + i)fnsW(s)). В глубине заштрихован­ной области W(5) имеет асимптотику 2е_а2^>1 (5= (ip — kzVох) Ikzvr)• В этой области решение очень быстро осциллирует и, возможно, обращается в нуль. В этом случае появляются затухающие колебания с такими значениями Re а) и Im о) <С 0 (| Im со | ^>kzvT), для которых, по крайней мере, одна из граничных точек попадает в заштрихованную об­ласть. Это условие является необходимым, так как выше было показано, что, если обе точки х = dt а лежат вне заштрихованного сектора, то зату­хающие колебания также невозможны. Однако затухающие колебания с | Im со | даже если они и существуют, должны давать малый

Вклад во временную асимптотику начальных возмущений (см. следующий раздел).

3. Эволюция начальных возмущений

Эволюция возмущений во времени определяется уравнениями (7) — (9). Нас будет интересовать асимптотическое значение фк(я, t) при t-+- 00, которое, как известно, определяется особенностями подынтеграль - пого выражения в (9). Обычно это полюса функции Грина, соответствую­щие собственным значениям частоты. В нашем случае, как и в ряде дру­гих задач о колебаниях плазмы (жидкости) с переменной скоростью, соб­ственные функции не составляют полной системы, при этом появляется

Новый тип элементарных решении — аналог волт ван Кампена, которые и определяют эволюцию начальных возмущен^ [6> 8-9].

Подынтегральное выражение в (9) зависит от комбина|рй р + 1кгУ0'х, р + ЬкгУо'хо, р ± 1кгУо а (ом. уравнения (4) —(6)). Поэтому при исследо­вании (9) удобно использовать рисунок, на котором изображена плоскость комплексного переменного Ькух + кф/кгУ(!. В частности, контур интегри­рования изобразится на этом рисунке линией, параллельной оси ординат и лежащей в правой полуплоскости. Функция Грина, в (7), (8) составлена лз решений однородных уравнений. Гидродинамическое уравнение (3) имеет особенность при х = 1р/кгУо. Поэтому при заданных х, х0 особен - - ности функции Грина расположены в точках р = —1кгУо'х, —1кгУо'х^ =FiA:гFo/a. Эти особенности устраняются учетом теплового разброса, однако при этом оказывается, что гидродинамическое приближение справедливо лишь вне заштрихованных секторов

Iаг%(р + ъкгУо’х) | < Зл/4',

1аг£(Р + 1кгУо'хо) | < Зя/4

И т. д. Несложные соображения показывают, что при не слишком большом времени, копда кги^<^, для подынтегрального выражения можно ис­пользовать гидродинамическое приближение, учитывая правило обхода точек ветвления разрезом, проведенным в левой полуплоскости.

Полное 'вычисление асимптотических выражений довольно громоздко. Мы продемонстрируем технику вычисления, оценив вклад в асимптотику сингулярностей при р = —1кгУо'х и р = —1кгУ0'х0. Будем считать также, что при £ = 0 возмущена лишь плотность плазмы в области х0 < х. В си­лу линейности задачи вклады в асимптотику от различных возмущений можно вычислить по отдельности. В рассматриваемом случае имеем

(1,г)= ио 5 ареР1£Е±(^-^}_. (16)

V ' - и/ 2л* у р + 1кгУ0'х0 у 1

—п а—гею “ 1

Здесь, используя абсолютную сходимость интегралов для достаточно боль­ших <т, мы поменяли порядок интегрирования. Функции g± составлены из решений однородного уравнения (см. (5)), которые выбраны в виде

2*у/>

<Ри(д) = — ,|,^(9) » з,,2±'’.

Г(± V + 1) <7-*-0

Из последнего выражения следует, что наибольший вклад в асимптотику внесут функции <$г(к1р/кгУъ + 1кх) и ^2(кр/кгУ0' + 1к1х0). При х —

— х0| <^;а имеем (см., например, [12])

(X, 0 = х

2л I р + 1кгУ0х0

~ ~2Г(~^Г7.)'(кгУо’— г°) )^+1 ехр 4 к*У°'(х + 1о)г|-

• |/у-1 у^-кгУо(х — *оН к. у„'(х — х0)г Л. (17)

Если кг\'(х — Х о) ^ | <С 1, то особенности можно считать слившимися и при вычислении асимптотики положить х = хо. Действительно, в этом

Случае из (17) имеем

Уравнения (17) —(19) справедливы при |х0 —х|<^а, очевидно, что вы­ражение типа (19) должно получиться и при х — х0| ~ а.

Таким образом, асимптотика <Рк(я, 0 в точке х складывается из возму­щений двух типов, соответственно, с частотами а) = кгУ0'хо ию = кгУ0'х. Здесь, как и раньше, х0 — точка нахождения «источника» (см. (3), (8)) и х — точка наблюдения. Вклады этих возмущений разделены при кгУо (х — х0)£|5> 1. Возмущение первого типа вызывается плоским слоем электронов, локализованным в точке хо. Этот слой модулирован с волно­вым вектором к= {0, ку, кг) и движется со скоростью Уог(хо) — Уо'хо. Он возбуждает волну, частота которой в лабораторной системе координат равна о = кгУо'хо. Поле такого слоя описывается функцией Грина СТр, к, х, (х) .

Возмущения второго типа с частотой а> = кгУ^х в определенной сте­пени связаны с использованием преобразования Лапласа. Действительно, решая задачу с начальными данными с помощью преобразования Лапла­са, мы предполагаем, что возмущения возникают мгновенно при I = 0. Разложение разрывной функции (времени в интеграл Фурье содержит все частоты, (поэтому при внезапном возникновении модулированного слоя электронов с координатой х =■ х0, - вообще говоря, должен (возбуждаться весь спектр частот, а не только частота, соответствующая локальной ско­рости дрейфа о = кгУ0'х0. В соответствии с этим даже при возмущении, локализованном в точке х0, правая часть (3) отлична от нуля для произ­вольных значений р, хотя возмущения с р = —1кгУо'хо и входят с наи­большим весом. В точке х Ф хо взаимная интерференция полей с ю Ф кгУо'х приводит к их уничтожению через «ремя £ » (кгУо'(х —

— х0))-1. Однако возмущения с частотой о ж кгУо'х резонируют с движе­нием плазмы в точке х, в результате для поля возмущения с ю = кгУо'х эта точка является точкой ветвления (см. (10), (13)). Точка ветвления и дает вклад в асимптотику (19).

Заметим, что в работах [в,8.|, где рассматривались сходные вопросы, учитывались только возмущения первого типа. Однако возмущения второ­го типа, вообще говоря, дают сравнимый, а в некоторых случаях и преоб­ладающий вклад в асимптотику. Его точная величина, в силу сказанного выше, должна определяться конкретными деталями процесса включения начального возмущения. Следовательно, точное вычисление асимптотиче­ских выражений в настоящем случае было бы нецелесообразным.

Возмущения первого типа входят в асимптотику чёрез интеграл Фурье типа

14 /КЭТФ. .V* П

В соответствии с [13] при кгУо'аЬ 2$> 1 его асимптотика также опреде­ляется ТОЧКОЙ ветвления функции }(х, Хо) при х = х0 (см. (19)). Вычис­ляя интеграл Фурье, находим, что вклад возмущений первого типа зату­хает со временем как г2''-2, где 0 < V < Уг (см. предыдущий раздел). Вклад возмущений второго типа также легко оценивается. Оказывается, что в данном случае именно он определяет асимптотику фк(х, I):

Фк(х,0«-р-лк(0)(^-Уо'<) ехр){— 1к, У„'х1). (20)

Аналогичным образом находится часть асимптотики фк(х, £), связанная с возмущением скорости Ук(х0, 0). В этом случае вклад возмущений пер­вого и второго типа по порядку величины одинаков:

Фк (д. I) & у Л ) ехр{— Ис^о’хг). (21)

В выражениях (20), (21) через Гск(0), ^к(О) обозначены некоторые сред­ние значения начальных возмущений плотности плазмы и ее скорости.

В предыдущем разделе мы нашли, что каждому значению к соответ­ствуют две собственные функции с частотами о) = 1ккгУ0'а. Для таких ча­стот функциональный определитель IV обращается в нуль, а функция Грина — в бесконечность. Однако если обычно собственным частотам соот­ветствуют полюса функции Грина, то здесь мы имеем точку ветвления. Эта особенность также дает вклад в асимптотику фк(х, 2) и при вычисле­нии необходимо учесть, что функции входящие в числитель функции Грина, также имеют точки ветвления при р = ±1кгУ0'а. Полный вклад этих особенностей в асимптотику по порядку (величины равен

Фк(г, 0 » [„ (0) + ° Уо'г ) ехр{=Р г^Уо'аг}.

(^2)

Если в начальный момент скорость плазмы возмущена вблизи грани­цы кгУо'{хо ± а)£| ^ 1, то затухание становится более медленным.

В этом случае комбинация кгкг1Уо^ входит в асимптотику (22) в степени

—V — Уг. Наконец, если возмущения отличны от нуля вблизи границ и наблюдение производится в этой же области | кгУ0 (х ± а) £ | 1, то для

Фк (х, £) имеем

4яе Г / к^оЧ -1 Ат1 Т^к (0) лг0 П

Фк(х, 0 » —(X ± а) [пк (0) (-^-) + - • у }

1 0 (23)

В заключение заметим, что мелкомасштабные возмущения с к1а!^> 1 ло­кализованы вблизи области первоначального возникновения на расстоя­ниях порядка 6х « кг* а.

На больших интервалах времени, когда кги^^>1, становятся сущест­венными малые интервалы по р (6р л кгит) и по х (Ьх « ит / К0'). В этом случае необходимо использовать кинетические выражения (см. (1), (7)). При учете теплового разброса подынтегральное выражение в (9) стано­вится аналитическим, и поэтому асимптотика фк(х, £) затухает быстрей любой степени г*1. Так, например,

1 Т°л, Г, е“т”’/2т 1/ 2лТ ( 2Г Л

■— <1реР‘с1и---- ——= У------------- ехр^ — к,2 — 1г.

2л1 Р + 1^ги ш I пг )

0—100

Собственные колебания, найденные в предыдущем разделе, имели частоту © = ±kzV0'a. При кинетическом рассмотрении значения частот могут измениться на величины порядка кгит. Не исключена возможность, что эти колебания станут нарастающими с Im со ^ kzvT. Следует отметить, что при kid 1 такие колебания, если они существуют, будут локализованы вблизи границ плазмы на расстояниях порядка Ьх ж кс1 и поэтому He - окажут влияния на эволюцию возмущений внутри плазмы.

Заключение

Таким образом, нами исследована устойчивость электронного потока и линейным профилем скорости в сильном продольном магнитном поле. В разделе 2 показано, что з гидродинамическом приближении мнимая часть частоты собственных колебаний в рассматриваемом случае равняет­ся нулю, а соответствующие собственные функции не составляют полной системы. В разделе 3 задача об эволюции произвольных начальных возму­щений решается методом преобразования Лапласа. Найдено, что началь­ные возмущения затухают асимптотически, как ^(0<а <3/г), и, сле­довательно, рассматриваемое течение является устойчивым.

За обсуждение работы авторы благодарны акад. М. А. Леонтовичу. Б. Б. Кадомцеву, В. В. Арсенину и Д. Д. Рютову.