Задача об эволюции начальных возмущений
В разд. 2 мы показали, что при выполнении условия (13) дифференциальное уравнение (12) не имеет собственных функций. Эта ситуация довольно необычна в теории колебаний плазмы. В то же время аналогичные эффекты характерны для теории колебаний идеальной жидкости; так, например, собственные функции отсутствуют в случае куэттовского течения [13]. Как указано в работах [2], это, однако, не означает, что для куэттовского течения задача с начальными данными не имеет решения, поскольку она сводится к задаче на собственные функции далеко не для всякого дифференциального уравнения. Действительно, произвольное начальное возмущение может быть разложено по собствен - нымсфункциям только в том случае, если они образуют полную систему, как, например, в случае самосопряженных несингулярных операторов (теорема Штурма—Лиувилля).
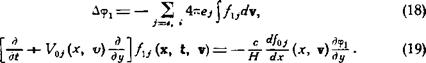
|
Используя для возмущенных величин, входящих в уравнения (18), (19), преобразование Фурье по у и Лапласа по t, например, для ^ имеем |
![]()
|
00 |
![]()
|
—00 00 О |
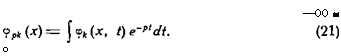
|
В результате уравнения (18), (19) принимают следующий вид |
![]()
|
/=«, і |
![]() Рассматриваемое нами уравнение (12) не принадлежит к этому классу; следовательно, в нашем случае для решения вопроса об эволюции произвольного начального возмущения также необходимо непосредственное рассмотрение задачи с начальными данными. Эта задача описывается следующей системой уравнений (см. разд. 1)
Рассматриваемое нами уравнение (12) не принадлежит к этому классу; следовательно, в нашем случае для решения вопроса об эволюции произвольного начального возмущения также необходимо непосредственное рассмотрение задачи с начальными данными. Эта задача описывается следующей системой уравнений (см. разд. 1)
Подставляя fj рк из уравнения (23) в уравнение (22), находим
TOC o "1-5" h z [а? ~ 2 л ^ ^ =
]=«. *
= — 2 4*еЛ<Лг/ 4(х, 0, у)0>ч-Л1/0^)-1. (24)
У=е, ♦ •>
Будем считать для простоты, что начальные возмущения имеют гидродинамический характер, т. е. что возмущена лишь плотность заряженных частиц, но не форма функции распределения в пространстве скоростей
/.?,*(*. 0, ) = п, к(х, 0)/0, (лг, т) П-) (х),
Где ПП] (.г) = | (х, г). Поскольку не зависит от угла в, интегри-
Рование по этому параметру производится так же, как и в разд. 1. В результате получаем
I j—в, »0 '
____ 00
= - 2 *{х’ °> "5 <*> [о» 1ку»у + {кУ’<>5г)ТЛ- (25)
В разд. 1 показано, что однородное уравнение (25) с правой частью, равной нулю, не имеет решений. Это свидетельствует об отсутствии самосогласованных колебаний плазмы. В этом случае, однако, возможны колебания, связанные с присутствием в начальный момент в плазме модулированных пучков заряженных частиц. Действительно, уравнение непрерывности, которое использовалось при получении уравнения (25),
Можно записать в форме ^---*-<1^ (/0Уг) = 0, откуда следует, что возмущение плотности заряженных частиц может вызываться как их движением в самосогласованных полях со скоростью у1г так и модулированными пучками с волновым вектором ку = к и скоростью 1/0у (при = к^У^). Для возмущений последнего типа имеем
^г = А = Со (ш — £1/0 (х, V)).
Очевидно, что произвольное возмущение начальной функции распределения /у к (х, 0, у) можно разложить по таким пучкам.
Для того чтобы найти решение неоднородного уравнения (25), используем функцию Грина—£>**„(*), которая, по определению, удовлетворяет уравнению
Здесь Ь — дифференциальный оператор, стоящий в левой части (25). Следуя работам Г2], выразим функцию Грина через решения однородного уравнения Ьурк, (л-)=0 ($=:1, 2)
(—(*/>)?+(*о/>) (х < *■>)•
?„*.(*)-{_ иг-^Лхр)? (чр) {х>х0). (г >
Здесь
?± (хр) - ?рк1 (*) (± °о) — 9рк2(х) <?р|с1 (± оо),
^=^7 ж=х = [?*1(-с°)?*(с°)-?м,(-»)?*(»)]Х
|
X |
![]() Д'1рк д<?Рк2 1
Д'1рк д<?Рк2 1
Ф 5 Журнал технической фнэнкн. N8 Ю, 1966 г.
Определенная таким образом функция Грина непрерывна и ограничена. Действительно, в силу отсутствия собственных функций у однородного уравнения (25), а также из-за линейной независимости функций Уркя(х) ни ОДИН из сомножителей, входящих в выражение для И?', не обращается в нуль, и, следовательно, величина В^“1 конечна. Функции Урки из которых составлены функции также ограничены повсюду на интервале (—со, со), в том числе и в особых точках, вблизи от которых имеем [12]
?рк. (х) = А,3г}Р (*_,) -+- Вш1 [х, Р (г,) 1п г у ■+- <2 (хД, (27)
Здесь — хеу, i4, В— постоянные величины; Р, (2 — полиномы от
*Гу, начинающиеся с нулевой степени. Выражение (27) для уркй справедливо при |*Гу| ^>г^у. В обратном случае |*у|^глу становятся существенными эффекты ларморовского радиуса, при учете которых особенности в уркв устраняются (см. разд. 1).
Используя функцию Грина, запишем решение уравнения (25) в виде •
00 00
TOC o "1-5" h z 9рк (*) = —} <1х^ркХ' (х) 2 (л:, 0) | (и) X
—00 ■]—*' о
X [(/>ЛУ* (Х0))2(кУ0 ^)2]'7’. (28)
Для того чтобы проследить за временной эволюцией начального
Возмущения, необходимо выполнить обратное преобразование Лапласа
А-4-»оо
?*(*. 0 = и 4**¥м(*>. (29)
А—»00
Причем эту операцию удобно проделать до интегрирования по с1ъ и с1х0 в уравнении (28).
Как известно, асимптотика выражений типа (29) при tсо определяется особенностями подынтегральной функции. В нашем случае особенности расположены в точках />1у =—Не]/0у(х0), р^ — —/£1/0у(х)»
С
В окрестности которых имеем Чркхъ{х) — “+" ^11п(р--- Рг); Ггркх0 (*> =
= С2(р — —Рг)* Наибольший вклад в асимптотику дает полюс
Первого порядка, учетом которого мы и ограничимся. При гт ^0 вели-
Чину — необходимо заменить на £(/>—/>х)2 Эта замена
Не затрудняет преобразования Лапласа, выполняя которое, получаем [1о]
Со
9к(х, /) = — Г Лг0 2 У-«Гу(*„), *.*.(*) X —00
X 4=ву. д (*„, 0) Е-'к7^‘ Ф, (X, /). (30)
Здесь величина Фу (х, £) равна
00
Фу (х, 0 = 2- | (х, v)Jл(kV0
О
/о— функция Бесселя нулевого индекса. При малых временах
Функция Фу равна Фу(/) = 1. В обратном случае t^(кV'Qr:l) 1 влияние
Эффектов ларморовского радиуса приводит к зависимости асимптотики
Срк(х, t) от вида функции распределения частиц по скоростям. Так,
M —тр3
Например, при f0j (v) = v в 2TJ
1 j
Ф,(t) = exp [_ (kV'r^tn (rlJ.
Если разброс по скоростям Дг>г меньше vT, то обрезание за счет эффектов ларморовского радиуса наступает при больших временах,
Когда kV' 1.
Таким образом, при учете ларморовского радиуса начальные возмущения затухают со временем, причем затухание усиливается с увеличением теплового разброса по скоростям. Оно возникает из-за того, что при гХт-7^=0 частицы с одной и той же координатой х имеют, вообще говоря, различные скорости дрейфа по ОК [см. (5)]; в результате модулированные пучки, из которых составлено возмущение, расплываются со временем. Заметим, что аналогичную природу имеет затухание Лан- дау И-
Для нахождения асимптотики cpfc (jc, t) нам остается вычислить интеграл по dx0 в уравнении (30). Если в начальный момент возмущение имело вид модулированного пучка, локализованного в точке х0 = аи rijk(x0, 0) = /1^0 (Х0 — ах), то из уравнения (30) находим
0 = — 2 4ltejg-nT, nlh).k, a,(x)rf, je-ttT‘^t<S>j(x, t). (31)
J=e, i
В этом случае затухание обязано только множителю Фу (/). Однако если начальное возмущение nJk(xQ, 0) является гладкой функцией от х0, то из-за того, что скорость дрейфа по О К зависит от х, отдельные пучки, из которых составлено первоначальное возмущение, будут смещаться со временем относительно друг друга. Интерференция возмущений, связанных с ними, должна привести к дополнительному затуханию.
При нахождении асимптотики cpfc (х, t) мы воспользуемся результатами работы [16]. Из рассмотрения проведенного в ней следует, что при (itVoAx)“1, где Ах — область локализации первоначального возмущения, 9к(х> 0 должен стремиться к нулю тем быстрее, чем лучше аналитические свойства предэкспоненциальной функции ф* (х0) =— ^ g-ikv0Jix.). к. х, Х
J=9, i
X (*) * 4тсвуИу* (*0, 0). В этом легко убедиться, интегрируя в (30) по частям нужное число раз. Так, при наличии скачка у функции ф, когда
У — С'*(хо — Ь), <?к‘—у e~ikY°ib)t. Если скачок испытывает производная ф', то ср* — Наконец, если функция ф аналитична, то cpfc стре
Мится к нулю быстрее, чем любая степень у.
В нашем случае л°, — гладкая функция и неаналитичность связана с функцией Грина, поскольку ее произйодная должна иметь разрыв при Х = х0, /(х0 + б) — ^'(^0 — ®) = 1- Интегрируя в (30) дважды по частям, получаем
2; Ar-einjAx’ °) .21/,2,2 ф; (*. t). (32)
T-+co. j=e, 0
Из (32) следует, что возмущение потенциала при /->оо в точке х связано с наличием модулированных пучков, находящихся только в этой точке. Вне области локализации пучков интерференция возмущений
Приводит к их уничтожению через время t^(kV„Ад:)-1, где Лд: размер области.
Заметим, что при t (кУ'0гхУ1у когда период пространственных осцилляций величины е~*кУо* много больше гл. (и поэтому эффекты лар - моровского радиуса еще не важны), у функции Грина имеется логарифмическая особенность вида (*■—jc0) Wi ( jc — д:0— / —l—) [см. (26), (27)].
Здесь в соответствии с правилами аналитического продолжения решения величина е положительна (г —> 0). Можно ожидать, что эта особенность даст свой вклад в асимптотику <р*(-*, /). Однако нетрудно показать, что вклад логарифмической особенности имеет вид /~2e~‘fc*VQ(—t) (9 = 1 при *<0 и 9=0 при /0), т. е. равен нулю. (При доказательстве полезно ввести функцию gl9 которая является аналитической и отличается от g лишь при xt близком к х0).
Как уже отмечалось, рассматриваемая нами задача близка по структуре к задаче об устойчивости плоско-параллельных течений идеальной жидкости. В частности, для куэттовского течения мы также получили бы асимптотику вида t~2e'*klat, которая отличается от асимптотики, полученной в работе [2], t~le-<kV°'. Причина расхождения на наш взгляд связана с неправильной оценкой интеграла типа (30) в этой работе.
Таким образом, нами показано, что если скорость электрического дрейфа меняется с расстоянием по линейному закону, а параметры плазмы определяются условиями (13), то собственные колебания отсутствуют и произвольные начальные возмущения потенциала оказываются, затухающими. При этом асимптотика возмущения при оо существенным образом зависит от эффектов, связанных с конечной величиной ларморовского радиуса, а через них и от конкретного вида функции распределения заряженных частиц.
Автор благодарен Б. Б. Кадомцеву за внимание к работе и полезные советы.
ПРИЛОЖЕНИЕ
Чтобы получить выражение для возмущенной плотности с учетом эффектов ларморовского радиуса, удобно использовать метод интегрирования по траекториям (см., например, [п])
О
= dtx*x (t, Г (0) (., ч). (Ш)
— 00
Здесь невозмущенная функция распределения /0 зависит от интегралов движения: полной энергии частицы s = -+- ея0 (х) и х-координаты
Vy
Ее ларморовского центра у] = х —. Значения г (/), y(t) берутся на
Траектории частицы, движущейся в скрещенных полях: магнитном и электрическом, направленных соответственно по OZ и ОХ. В дальнейшем нам понадобится только выражение для х-координаты частицы
С точностью до членов : x(t) = x(0)—-g - sin 9|*, где 9 (f) = 9 (0)—Qt—
Угол между осью ОХ и направлением скорости частицы.
Усредняя по времени х-компоненту уравнения движения, нетрудно получить выражение для средней скорости дрейфа заряженной частицы по OY
^ = W (&), = «»• <2П)
Здесь учтено приведенное выше выражение для х(/), а также то
1 т
Обстоятельство, ЧТО <ЛГ/, = 2Г * l-rT^њ^O.
С учетом (2П) выражение для срх (/) принимает следующий вид
Используя его, находим
Если разброс по скоростям не слишком мал | V In л01, то
Выражение (ЗП) можно преобразовать к виду
= ТГ J dy ZT v) [~ 1“ — Vw ^ т)] 1 (4П)
Рл dfQ аfQ t а fQ
Здесь учтено равенство -+- вср0 .
В основном тексте мы, пользуясь тем, что /0(x, v) в нулевом приближении по ларморовскому радиусу не зависит от угла 0, вычислили в (4П) интеграл по </0, а для интеграла по dv применили следующую форму записи
00 00
I vdv'^F{v) = ^{F(v)/< где <f(«)/ = (^) ‘J vdv^F(v).
О о
В случае больцмановского распределения частиц в электрическом поле
Яю: »(Мх)
А(х< v) = n0(x)e - т, где па(х) = Ал(х) е т .
Последнее выражение принимает особенно простой вид
00 ШИ1
= ^ vdve lT F{v).
О
Для наших целей оказалось достаточным учесть влияние эффектов ларморовского радиуса на скорость невозмущенного дрейфа. Полный учет этих эффектов при наличии электрического поля можно найти в работах [*•п]. Однако уравнение желобковых колебаний, найденное в[8], неприменимо в окрестности особых точек, так как получено в предположении I и) — IW-